一。Getting Start
Again and again,until you master it.早在接触java.util包的时候,我们都会去阅读ArrayList,甚至也会去阅读HashMap(毕竟面试必考)。然而我们有可能”知道“了它们,却不一定”理解“它们。为了更深入的了解它们,笔者决定再细读一遍,然后将其写成博客,以接近理解的状态。(学习的最好方式就是将其教授给他人)
我们知道目前jdk甚至到了11都已投入生产的情况了,鉴于目前工作应用的关系我将使用jdk8的源码作为解析。
二。HashMap
作为使用空间换时间的典型案例,这种数据结构拥有这O(1)+O(len(List))的读效率和写效率,在数据结构基础课上介绍的哈希表,就是此物。
它拥有以下结构。

作为数据结构基础,它的结构是外层一个数组,数组中存着具体的元素Node,Node是单链表基本元素。
它在查找元素的O(1)的效率在于利用了作为key元素的hash值(那是一种标记Java元素的long型数据),查询通过(hash & len - 1)的方式计算数组下标,然后遍历链表(O(len-1))找到key对应的Node中的value。
因为一些原因(懒),1.7的代码就不从IDE中阅读了,借鉴了这位仁兄的博客:https://www.cnblogs.com/williamjie/p/9358291.html
jdk1.7的hashmap易于理解,put的时候找到链表中是否存在key,存在则替换value不存在就链在最后(尾插法);而它在resize的时候,会遍历数组对数组上链表的每一个元素进行重新hash,并放到扩容后的数组上(头插法),所以被链接到同一个位置上的元素是倒序的。
接下来我们进入1.8的HashMap源码阅读。
对一个类的了解,就从他怎么来的开始吧。(构造函数)
tips:打开IDEA,选择view的tool查看structure,便于对类有个全局感
打开HashMap源码,在左侧窗口中看到他的成员变量,以及构造函数,成员函数。
我们看到四个构造函数,无参构造仅仅是把负载因子设为默认值(0.75)

而使用initialCapacity的构造函数与initialCapacity & loadFactor的构造函数,操作是一样的。
解析:(1)如果初始化容量是一个负数,则会抛出不合法异常;
(2)初始化容量大于最大整型值,则使用最大整型值;
(3)负载因子是负数或者NaN(前端经常见到这个)会抛出不合法异常
(4)将负载因子赋予本对象的负载因子属性并计算threhold,最后赋予本对象threhold属性。


最后一个构造函数,加载默认负载因子,并将传入Map中的元素拷贝到本实例的数组存储中。

在jdk1.8的HashMap中,它们遵循一个原则:HashMap的数组长度是2的n次方,所以在你使用初始化容量的时候,它会计算离你这个数最近的2的n次方这个数值。
而计算方法也是非常的精彩(sao)

这里有一个位运算(>>>),它表示的是无符号右移,在二进制(例如0100 >>> 1 = 0010)操作中,将它们每一位右移,高位使用0补齐。这个算法目的在于将cap最高位的左边一位置为1,其他置为0(比如01011 -> 10000)。
以01011为例:(1)01011 - 1 = 01010
(2) 01010 | 00101 = 01111
(3)01111 | 00011 = 01111
(4)01111 | 00000 = 01111
(5)...(后边都是00000了)
(6)在return的那一步,表示的是如果 n < 0 则返回1,也就是cap原本就为0的情况,否则判断n是否为整型最大值,如果不是则加1(10000);这样就找出了最接近cap的2次幂的值。
至于为什么最后只移位16,因为一个int值只有4个byte(32个bit,也就是32个0101),而正数负数使用一个符号位,so,int的MaxValue = 2的31次方 - 1。
接下来我们进入put方法的阅读。
/** * Associates the specified value with the specified key in this map. * If the map previously contained a mapping for the key, the old * value is replaced. * * @param key key with which the specified value is to be associated * @param value value to be associated with the specified key * @return the previous value associated with <tt>key</tt>, or * <tt>null</tt> if there was no mapping for <tt>key</tt>. * (A <tt>null</tt> return can also indicate that the map * previously associated <tt>null</tt> with <tt>key</tt>.) */ public V put(K key, V value) { return putVal(hash(key), key, value, false, true); } /** * Implements Map.put and related methods * * @param hash hash for key * @param key the key * @param value the value to put * @param onlyIfAbsent if true, don't change existing value * @param evict if false, the table is in creation mode. * @return previous value, or null if none */ final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; Node<K,V> p; int n, i; if ((tab = table) == null || (n = tab.length) == 0) n = (tab = resize()).length; if ((p = tab[i = (n - 1) & hash]) == null) tab[i] = newNode(hash, key, value, null); else { Node<K,V> e; K k; if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; else if (p instanceof TreeNode) e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); else { for (int binCount = 0; ; ++binCount) { if ((e = p.next) == null) { p.next = newNode(hash, key, value, null); if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st treeifyBin(tab, hash); break; } if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; p = e; } } if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; if (++size > threshold) resize(); afterNodeInsertion(evict); return null; }
按我们的理解,它的主题思想应该是(寻找下标->处理冲突->尾差法),让我们具体看看。
我们最常用的put(k,v)形式,实际调用的是putVal,onlyIfAbsent这个参数为true就不会改变已经存在节点的值,evict这个参数暂时没关注(注释表明它为false才生效)
putVal第一行,声明了所需要的参数:tab(指向容器的对象数组),p(指向对应位置的数组元素),n(table的length),i(下标位置)
(1)它的第一个if条件,表示如果table(持有的对象数组)为空或者长度为0,即没有初始化,它就会触发一下resize,并返回一个长度,而这个长度n,如果你传入了initialCapacity则会计算出最接近这个值的取上界的2次幂,如果未传入则使用默认的值16。
(2)好的,我们知道了第一个条件,然后它紧接着又是一个if,计算出table的对应位置是否为空,如果为空,easy,直接将这个k,v对new一个Node存储起来。
这个if的另一个分支,else,表示的是如果产生了哈希冲突,即这个位置已经存在链表结点;它在处理这个情况的时候很仔细,它先是检查头结点是否和传入的key相等(这个检查包括hash是否相等,k的值是否相等),如果相等则将数组上的元素赋予e以后使用;
它的下一个分支,表示它这个节点是个树的根节点,则将进入红黑树的插入操作(这步不仔细读了)
最后一种情况就是遍历链表,比对每一个元素,在break的时候,拿到的那个节点就是后续需要操作的e;这里有一种情况,就是链表长度达到阈值8,则将链表转化为红黑树,
在下一步,进行清算,如果e不为空,onlyIfAbsent是允许你改变值的,就将e节点的value改变为你传入的value,然后返回老的值(oldValue)。
最后几行先是将modCount加一下,然后在判定size是否大于threshold,如果大于阈值,则resize。
到此我们已经解读完毕。
接下来我们将进入另一个至关重要的方法:resize,因为它是HashMap的一个重要的过程(扩容)
/** * Initializes or doubles table size. If null, allocates in * accord with initial capacity target held in field threshold. * Otherwise, because we are using power-of-two expansion, the * elements from each bin must either stay at same index, or move * with a power of two offset in the new table. * * @return the table */ final Node<K,V>[] resize() { Node<K,V>[] oldTab = table; int oldCap = (oldTab == null) ? 0 : oldTab.length; int oldThr = threshold; int newCap, newThr = 0; if (oldCap > 0) { if (oldCap >= MAXIMUM_CAPACITY) { threshold = Integer.MAX_VALUE; return oldTab; } else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY) newThr = oldThr << 1; // double threshold } else if (oldThr > 0) // initial capacity was placed in threshold newCap = oldThr; else { // zero initial threshold signifies using defaults newCap = DEFAULT_INITIAL_CAPACITY; newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); } if (newThr == 0) { float ft = (float)newCap * loadFactor; newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? (int)ft : Integer.MAX_VALUE); } threshold = newThr; @SuppressWarnings({"rawtypes","unchecked"}) Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; table = newTab; if (oldTab != null) { for (int j = 0; j < oldCap; ++j) { Node<K,V> e; if ((e = oldTab[j]) != null) { oldTab[j] = null; if (e.next == null) newTab[e.hash & (newCap - 1)] = e; else if (e instanceof TreeNode) ((TreeNode<K,V>)e).split(this, newTab, j, oldCap); else { // preserve order Node<K,V> loHead = null, loTail = null; Node<K,V> hiHead = null, hiTail = null; Node<K,V> next; do { next = e.next; if ((e.hash & oldCap) == 0) { if (loTail == null) loHead = e; else loTail.next = e; loTail = e; } else { if (hiTail == null) hiHead = e; else hiTail.next = e; hiTail = e; } } while ((e = next) != null); if (loTail != null) { loTail.next = null; newTab[j] = loHead; } if (hiTail != null) { hiTail.next = null; newTab[j + oldCap] = hiHead; } } } } } return newTab; }
(1)进行resize之前,我们需要准备一些材料(老的table内存地址,老数组的长度,老扩容阈值等);
(2)如果是正常扩容,则进入第一个条件;在第一个条件中,如果达到整型上界,则直接返回,不会再resize,并且threshold也会赋予上界值,如果未达上界,则进行左移位,这个时候只有当新的容量长度大于DEFAULT(也就是16)的时候才会将newThr赋值为原先的2倍;
(3)第二个条件就是将threshold赋予新容量,这种情况是init传入非零值的时候;
(4)最后一个条件是init传入0的时候,采用默认容量和threshold;
(5)接下来这个if的情况就只有这个红框if不成立的情况了,将重新计算newThr;

(6)接下来就是简单的new一个新的数组,并赋值给老的地址;
(7)如果老数组是存在的(也就是不是初次resize),这个时候需要对原数组的元素进行重新映射;
方法就是遍历原数组,分为如果是孤立节点则直接赋值,如果是红黑树则进行红黑树处理,如果是链表,则进行一些特殊的处理(这个操作骚得我闪到腰);
在讲解这个方法之前,我查阅了别人解读的文章,大体上说这个方法是推出这个链表上的元素:映射在新数组的同样位置或者同样位置加上旧数组长度的位置;
至此我做了个实验;
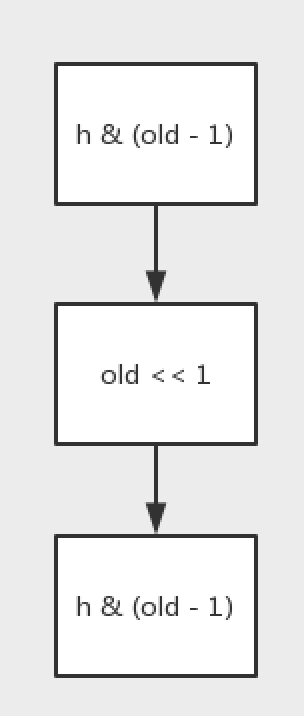
使用了一些作为案例进行计算,并不是所有的数都适用这种规则。
int[] hashcode = {5,17,23,33}; int old = 10; for(int h : hashcode){ System.out.println(h & (old - 1)); } System.out.println("rehash"); old = old << 1; for (int h : hashcode){ System.out.println(h & (old - 1)); }

只有2的n次方才适用这种策略,因为2的n次方,在二进制中只占用1位1,举个例子会比较清楚(假设原长度为16<10000>,它的扩容16 << 1 = 32<100000>,而真正确定下标的算法是 h & len - 1,也就是决定下标的位数在于比长度最高位低的所有位;比如 5<00101> & 16-1<01111> = 00101,21<10101> & 16-1<01111> = 00101,他们产生了冲突必然成为链表;而进行扩容后16->32,5<00101> & 32-1<011111> = 00101,而21<10101> & 32-1<011111> = 10101,这个时候它相对于以前就加上了16,原因就是长度扩容之后,& 的那位数多了一位二进制1,如果原来的哈希值含有这个位1,则就会加上老数组的长度)
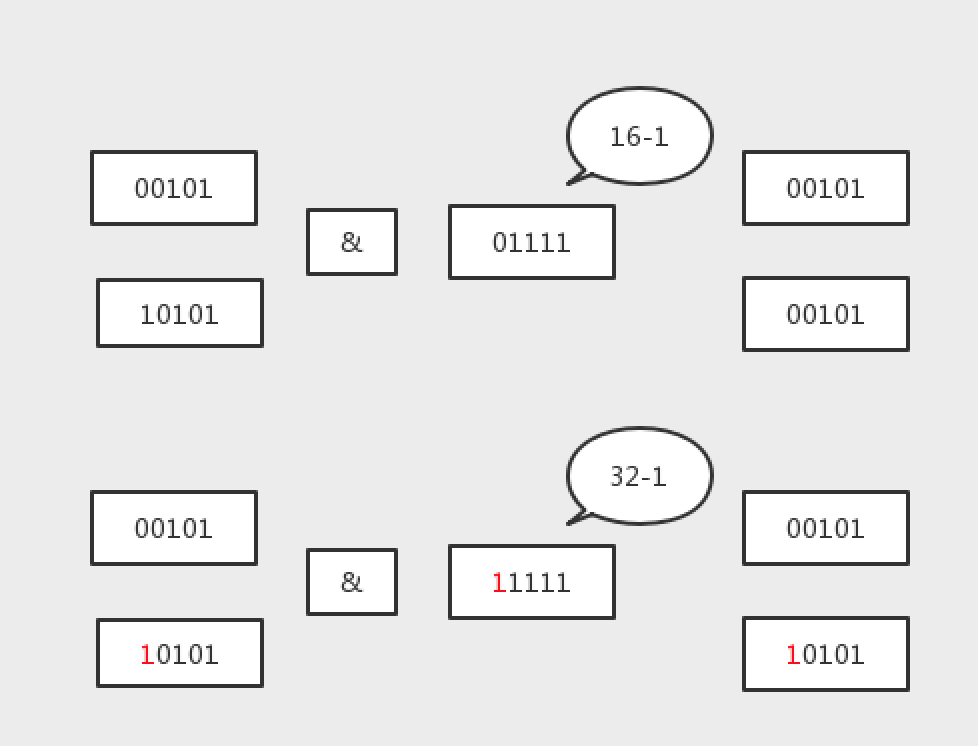
所以,它第一步就会做与原数组长度&一下,为了确定那个位是否为0,为0保持原位,为1加上原数组长度;它分别将两条链表构造完成之后,再赋值到新数组位置上,这样出来的元素就不是倒叙的了;
要说他比1.7有什么提升么,就是一个是倒置一个是顺序放置吧;复杂度应该没太大变化。(但是骚是骚了点)
至此,HashMap中最难以理解的部分全部都解析完毕。
三。ConcurrentHashMap
好,我们顺势进入CHM的阅读(HashTable那货没什么价值)----(但是这货真难啃)
(老子读了很久,最不理解的就是这些个位运算了!对sizeCtl又是一知半解,真难!)
我们就忘了1.7的segment吧,看看1.8的实现,1.8比起1.7的分段锁,它把锁的粒度变得更细了,细到获取的是头结点的对象锁。
构造方法还需要看吗?走读一下吧。
/** * Creates a new, empty map with an initial table size * accommodating the specified number of elements without the need * to dynamically resize. * * @param initialCapacity The implementation performs internal * sizing to accommodate this many elements. * @throws IllegalArgumentException if the initial capacity of * elements is negative */ public ConcurrentHashMap(int initialCapacity) { if (initialCapacity < 0) throw new IllegalArgumentException(); int cap = ((initialCapacity >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY : tableSizeFor(initialCapacity + (initialCapacity >>> 1) + 1)); this.sizeCtl = cap; }
一如既往去校验init参数的合法性,并将其转化为最接近的2的n次方,真正去new数组还是在putVal里。
putVal读起来真吃力,因为里面含有多线程操作的场景(很多时候想象力有限)。
/** * Maps the specified key to the specified value in this table. * Neither the key nor the value can be null. * * <p>The value can be retrieved by calling the {@code get} method * with a key that is equal to the original key. * * @param key key with which the specified value is to be associated * @param value value to be associated with the specified key * @return the previous value associated with {@code key}, or * {@code null} if there was no mapping for {@code key} * @throws NullPointerException if the specified key or value is null */ public V put(K key, V value) { return putVal(key, value, false); } /** Implementation for put and putIfAbsent */ final V putVal(K key, V value, boolean onlyIfAbsent) { if (key == null || value == null) throw new NullPointerException(); int hash = spread(key.hashCode()); int binCount = 0; for (Node<K,V>[] tab = table;;) { Node<K,V> f; int n, i, fh; if (tab == null || (n = tab.length) == 0) tab = initTable(); else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) { if (casTabAt(tab, i, null, new Node<K,V>(hash, key, value, null))) break; // no lock when adding to empty bin } else if ((fh = f.hash) == MOVED) tab = helpTransfer(tab, f); else { V oldVal = null; synchronized (f) { if (tabAt(tab, i) == f) { if (fh >= 0) { binCount = 1; for (Node<K,V> e = f;; ++binCount) { K ek; if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { oldVal = e.val; if (!onlyIfAbsent) e.val = value; break; } Node<K,V> pred = e; if ((e = e.next) == null) { pred.next = new Node<K,V>(hash, key, value, null); break; } } } else if (f instanceof TreeBin) { Node<K,V> p; binCount = 2; if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key, value)) != null) { oldVal = p.val; if (!onlyIfAbsent) p.val = value; } } } } if (binCount != 0) { if (binCount >= TREEIFY_THRESHOLD) treeifyBin(tab, i); if (oldVal != null) return oldVal; break; } } } addCount(1L, binCount); return null; }
在读这些代码之前,我们需要具有自旋CAS的基础。
所谓自旋CAS,就是循环CAS的意思,直到成功,这个做法在AQS中大量使用。CAS,就是一种乐观锁的使用方法,在update值的时候,需要它的expect与内存值相等。
好的,putVal开头,先是判断这个key和value的非空性;
之后,计算一下hash(这个位运算没看懂)
接下来进入到自旋中,每次循环都会将table拷贝到工作线程tab中;情况依然分为几个:(1)表未初始化;(2)算出下标位置为空;(3)扩容中;(4)形成了链表(R-B tree);
我们先看initTable方法:
/** * Initializes table, using the size recorded in sizeCtl. */ private final Node<K,V>[] initTable() { Node<K,V>[] tab; int sc; while ((tab = table) == null || tab.length == 0) { if ((sc = sizeCtl) < 0) Thread.yield(); // lost initialization race; just spin else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { try { if ((tab = table) == null || tab.length == 0) { int n = (sc > 0) ? sc : DEFAULT_CAPACITY; @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; table = tab = nt; sc = n - (n >>> 2); } } finally { sizeCtl = sc; } break; } } return tab; }
依然是一个自旋CAS的思路,由于初始化只需要一个线程做就好了,如果检查到sizeCtl小于0则表示已经有线程在初始化了,则让出CPU,Thread.yield();而如果你是负责初始化的线程,首先CAS sizeCtl 的值,将其设为-1,此时sizeCtl原来是在初始化时候设置的2次幂的长度,它将它拷贝到线程工作内存sc中,将sc作为初始化长度n创造一个数组,并赋予table;sc = n - (n>>>2),不知道啥意思,不过这个会作为下次resize的阈值,最终将这个sc赋予sizeCtl;(这里面还用了双检锁的思维)初始化成功会返回tab;
static final <K,V> boolean casTabAt(Node<K,V>[] tab, int i, Node<K,V> c, Node<K,V> v) { return U.compareAndSwapObject(tab, ((long)i << ASHIFT) + ABASE, c, v); }
它的第二段,如果tableAt对应位置取出来为null(这里还用了原子型获取对象),则会CAS设置节点值;这里的位运算,首先我们数组的内存首地址和具体值之间间隔了一个ABASE字节,这个ABASE是通过usafe的接口获取的;然后这个ASHIFT的计算,有点绕;
ABASE = U.arrayBaseOffset(ak); int scale = U.arrayIndexScale(ak); if ((scale & (scale - 1)) != 0) throw new Error("data type scale not a power of two"); ASHIFT = 31 - Integer.numberOfLeadingZeros(scale);
通过上面的计算,ASHIFT其实是指长度是2的多少次方这个次数;在二进制的乘法里,一个数乘以2的多少次方,其实就是左移多少位;在首地址+填充位+数据具体位置,就可以找到具体的元素位置了,最后CAS上去;
接下来第三种情况,就是在CMH做扩容时候,会将对应位置上的元素替换为一种特殊节点,它上面的hash值是-1,这时候会进入帮助扩容的方法;扩容我们到后边读到transfer再具体分析;
然后最后一种情况,来个双检锁,这里和hashmap就一样了,不是跟在后面就是比对节点hash值和key,更新value;如果是树节点,则做树操作;
最后在插入节点之后有一个binCount,表示当前数组位置的链表(树)长度,如果达到阈值TREEIFY_THRESHOLD,则进行扩容或者是树转换;(竟然是通过单个位置是否过长来resize)
/* ---------------- Conversion from/to TreeBins -------------- */ /** * Replaces all linked nodes in bin at given index unless table is * too small, in which case resizes instead. */ private final void treeifyBin(Node<K,V>[] tab, int index) { Node<K,V> b; int n, sc; if (tab != null) { if ((n = tab.length) < MIN_TREEIFY_CAPACITY) tryPresize(n << 1); else if ((b = tabAt(tab, index)) != null && b.hash >= 0) { synchronized (b) { if (tabAt(tab, index) == b) { TreeNode<K,V> hd = null, tl = null; for (Node<K,V> e = b; e != null; e = e.next) { TreeNode<K,V> p = new TreeNode<K,V>(e.hash, e.key, e.val, null, null); if ((p.prev = tl) == null) hd = p; else tl.next = p; tl = p; } setTabAt(tab, index, new TreeBin<K,V>(hd)); } } } } }
如码所示,如果数组长度小于64,就扩容;否则将其转换为树结构;
最后一个putVal里面的方法,就是addCount;
/** * Adds to count, and if table is too small and not already * resizing, initiates transfer. If already resizing, helps * perform transfer if work is available. Rechecks occupancy * after a transfer to see if another resize is already needed * because resizings are lagging additions. * * @param x the count to add * @param check if <0, don't check resize, if <= 1 only check if uncontended */ private final void addCount(long x, int check) { CounterCell[] as; long b, s; if ((as = counterCells) != null || !U.compareAndSwapLong(this, BASECOUNT, b = baseCount, s = b + x)) { CounterCell a; long v; int m; boolean uncontended = true; if (as == null || (m = as.length - 1) < 0 || (a = as[ThreadLocalRandom.getProbe() & m]) == null || !(uncontended = U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))) { fullAddCount(x, uncontended); return; } if (check <= 1) return; s = sumCount(); } if (check >= 0) { Node<K,V>[] tab, nt; int n, sc; while (s >= (long)(sc = sizeCtl) && (tab = table) != null && (n = tab.length) < MAXIMUM_CAPACITY) { int rs = resizeStamp(n); if (sc < 0) { if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0) break; if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) transfer(tab, nt); } else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) transfer(tab, null); s = sumCount(); } } }
这个方法通过一堆繁琐的操作,计算元素总数,然后判断是否需要resize;(看得累,都是对sizeCtl的状态转换);
由此我们可以看出,每次新增元素的时候,会调用addCount方法判断是否扩容,所以扩容时机总的来说是在addCount的时候,当然前边判断树节点的时候,也会触发扩容,不过是length<64的时候才会。
接下来再看两个方法就能对CMH有一个清晰的轮廓了。
/** * Tries to presize table to accommodate the given number of elements. * * @param size number of elements (doesn't need to be perfectly accurate) */ private final void tryPresize(int size) { int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY : tableSizeFor(size + (size >>> 1) + 1); int sc; while ((sc = sizeCtl) >= 0) { Node<K,V>[] tab = table; int n; if (tab == null || (n = tab.length) == 0) { n = (sc > c) ? sc : c; if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { try { if (table == tab) { @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; table = nt; sc = n - (n >>> 2); } } finally { sizeCtl = sc; } } } else if (c <= sc || n >= MAXIMUM_CAPACITY) break; else if (tab == table) { int rs = resizeStamp(n); if (sc < 0) { Node<K,V>[] nt; if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0) break; if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) transfer(tab, nt); } else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) transfer(tab, null); } } }
/** * Moves and/or copies the nodes in each bin to new table. See * above for explanation. */ private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) { int n = tab.length, stride; if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE) stride = MIN_TRANSFER_STRIDE; // subdivide range if (nextTab == null) { // initiating try { @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1]; nextTab = nt; } catch (Throwable ex) { // try to cope with OOME sizeCtl = Integer.MAX_VALUE; return; } nextTable = nextTab; transferIndex = n; } int nextn = nextTab.length; ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab); boolean advance = true; boolean finishing = false; // to ensure sweep before committing nextTab for (int i = 0, bound = 0;;) { Node<K,V> f; int fh; while (advance) { int nextIndex, nextBound; if (--i >= bound || finishing) advance = false; else if ((nextIndex = transferIndex) <= 0) { i = -1; advance = false; } else if (U.compareAndSwapInt (this, TRANSFERINDEX, nextIndex, nextBound = (nextIndex > stride ? nextIndex - stride : 0))) { bound = nextBound; i = nextIndex - 1; advance = false; } } if (i < 0 || i >= n || i + n >= nextn) { int sc; if (finishing) { nextTable = null; table = nextTab; sizeCtl = (n << 1) - (n >>> 1); return; } if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) { if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT) return; finishing = advance = true; i = n; // recheck before commit } } else if ((f = tabAt(tab, i)) == null) advance = casTabAt(tab, i, null, fwd); else if ((fh = f.hash) == MOVED) advance = true; // already processed else { synchronized (f) { if (tabAt(tab, i) == f) { Node<K,V> ln, hn; if (fh >= 0) { int runBit = fh & n; Node<K,V> lastRun = f; for (Node<K,V> p = f.next; p != null; p = p.next) { int b = p.hash & n; if (b != runBit) { runBit = b; lastRun = p; } } if (runBit == 0) { ln = lastRun; hn = null; } else { hn = lastRun; ln = null; } for (Node<K,V> p = f; p != lastRun; p = p.next) { int ph = p.hash; K pk = p.key; V pv = p.val; if ((ph & n) == 0) ln = new Node<K,V>(ph, pk, pv, ln); else hn = new Node<K,V>(ph, pk, pv, hn); } setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true; } else if (f instanceof TreeBin) { TreeBin<K,V> t = (TreeBin<K,V>)f; TreeNode<K,V> lo = null, loTail = null; TreeNode<K,V> hi = null, hiTail = null; int lc = 0, hc = 0; for (Node<K,V> e = t.first; e != null; e = e.next) { int h = e.hash; TreeNode<K,V> p = new TreeNode<K,V> (h, e.key, e.val, null, null); if ((h & n) == 0) { if ((p.prev = loTail) == null) lo = p; else loTail.next = p; loTail = p; ++lc; } else { if ((p.prev = hiTail) == null) hi = p; else hiTail.next = p; hiTail = p; ++hc; } } ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) : (hc != 0) ? new TreeBin<K,V>(lo) : t; hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) : (lc != 0) ? new TreeBin<K,V>(hi) : t; setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true; } } } } } }
第一个方法tryPresize是在树转换中<64长度调用的,把n扩容n<<1长度;while中判断sizeCtl是否大于0,如果大于则开始扩容,这里又搞了一段init;然后判断下这个c和sc的关系,是否结束;最后这个有两种情况,如果存在nextTable,如果不存在(不是扩容过程)则直接返回了;(没啥耐心看sizeCtl的状态了)

这两个地方就是告诉transfer是否需要new一个nextTable;
然后我们重点看transfer方法;它的扩容数据搬运思路是,一个线程申请一个区间,从大到小(比如有64长度,默认情况下一个线程获取16个长度,那么公共变量就是64,申请了一次变为48,表示它要处理48-63区间的数据,如果为0则申请不到区间,可以退下了);占位符的意思是,如果数据迁移完成,put的时候会检查是否hash为-1,如果是就来帮助扩容;bound是处理区间的下界;
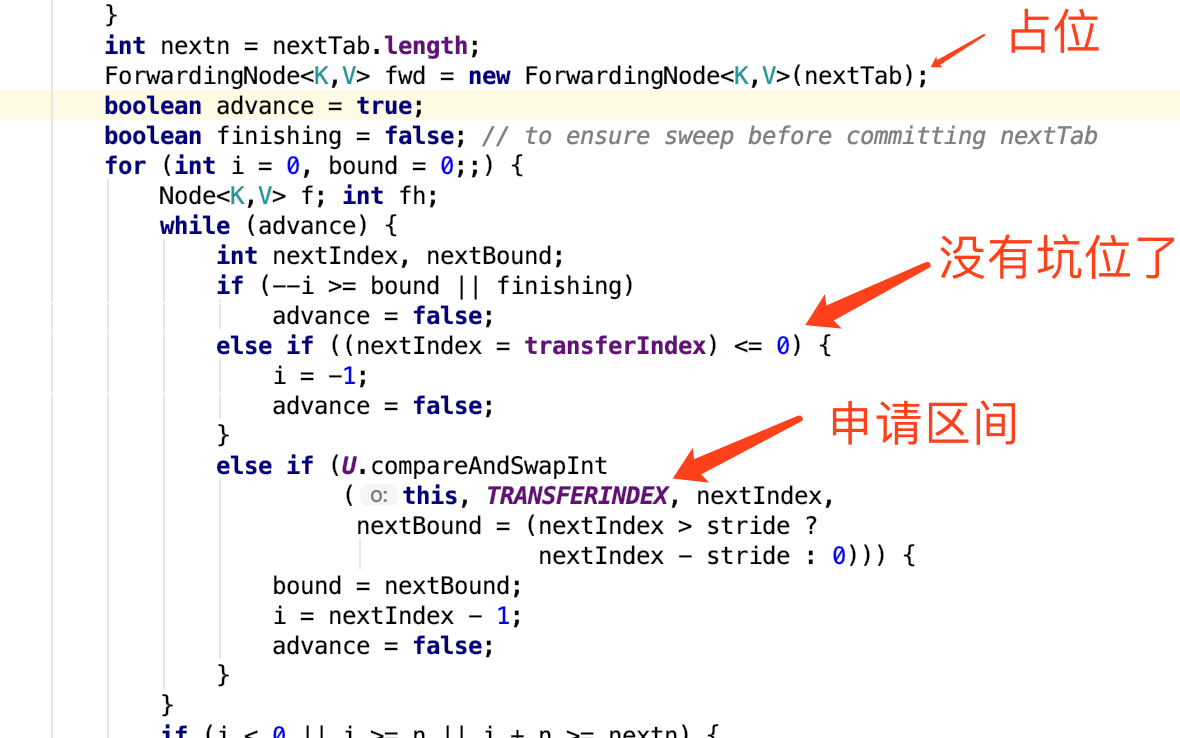
这里有根据cpu线程数来计算每个线程需要处理的数据量;



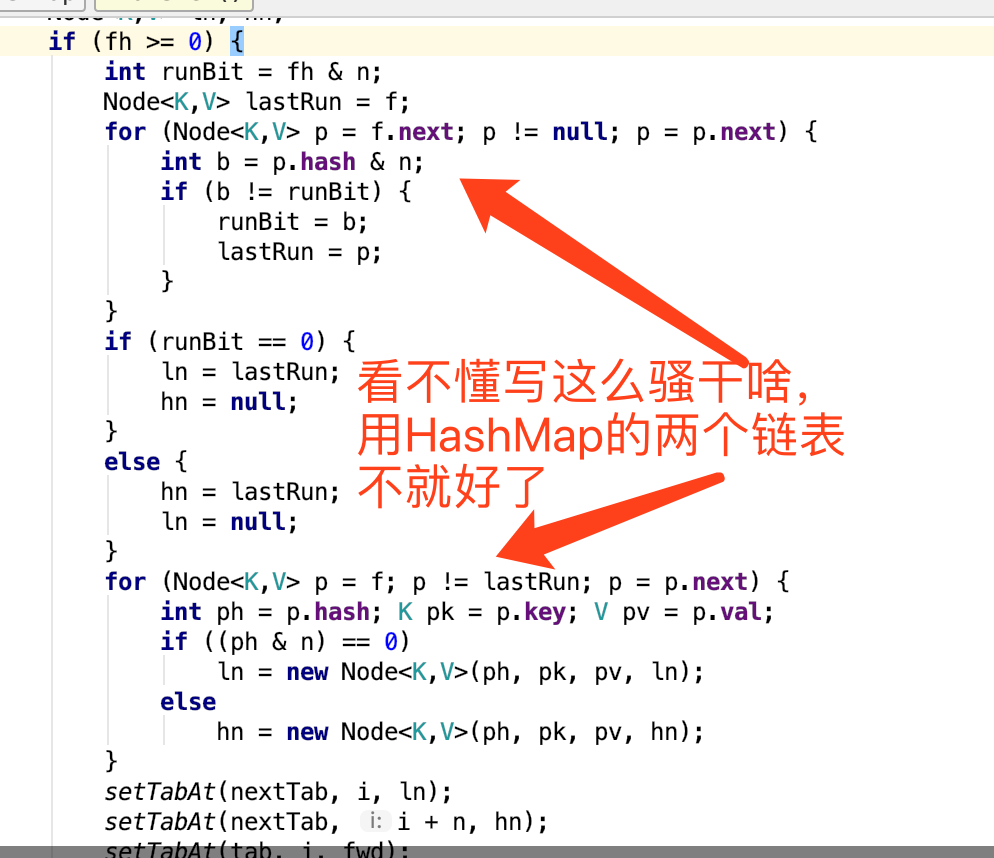
总的来说,还是以前的思路,&那个位数是0还是1,是原位还是+n,做完之后,将原来数组设置为ForwardingNode。做完之后,正在put的就知道你在扩容了,就不会往老数组写入数组了,保证了一致性;

In conclusion,1.8的CMH是通过自选CAS进行插入、扩容等操作,并通过识别sizeCtl来协调各种过程,如何保证一致性呢?在未扩容的情况,非常明朗,对象锁或者是CAS,这样有效解决了冲突;最难想象的是扩容和插入并行的时候,想象一下,你搞了一个newTable,在做数据迁移,你拿到了一个位置a(加锁的),扩容一直在申请锁,一旦申请到了,会将数据迁移到新数组a或者a+n位置,这时将老数组标记为-1(MOVE);此时putVal的自旋中,如果table还是老地址,则拿到对应位置是MOVE,则就感知到它正在扩容了,就会去帮着干,最终拿到扩容后的tab地址;再申请锁,再双检,最后才是插入链表。
四。LinkedHashMap
由此看,它是HashMap的一个子类,它的结构除了整体上是个数组+链表之外,彼此元素间还是个双端链表,它保存了插入顺序;
public class LinkedHashMap<K,V> extends HashMap<K,V> implements Map<K,V>
/** * HashMap.Node subclass for normal LinkedHashMap entries. */ static class Entry<K,V> extends HashMap.Node<K,V> { Entry<K,V> before, after; Entry(int hash, K key, V value, Node<K,V> next) { super(hash, key, value, next); } }
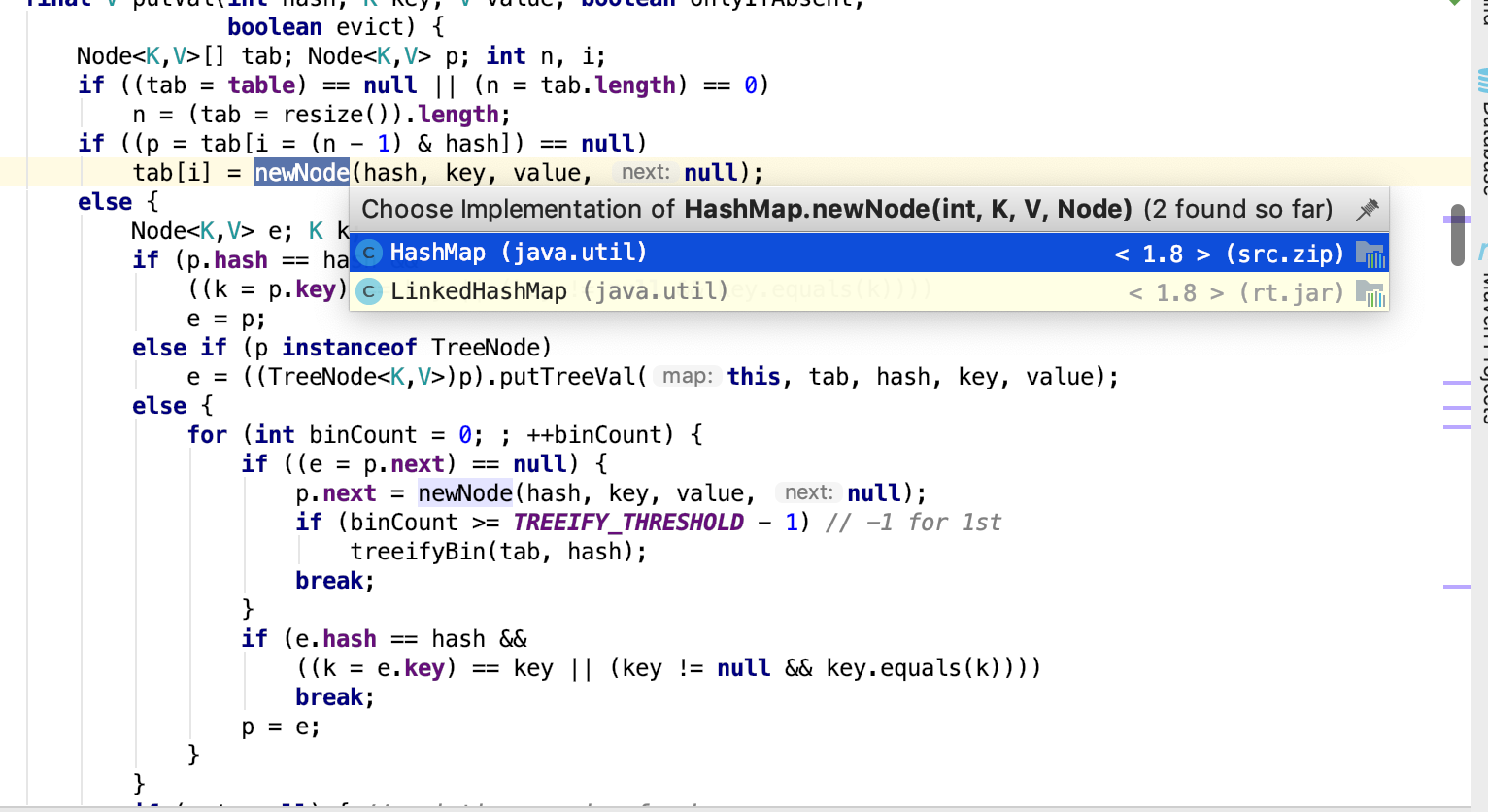

扩展性真好,只需要重写一些方法,就可以在基础上改变结构;在明白HashMap的基础上,这个数据结构也会变得更容易理解了;主要是遍历的时候不一样。
五。练习
首先我们的Map会有这样的一种结构,作为元素类的Node,以及持有数组Node[]的Map类。
public class DataStructure<K,V> implements Serializable { private volatile Node<K,V>[] tab; private final int DEFAULT_CAPACITY = 1 << 4; public DataStructure(){ tab = new Node[DEFAULT_CAPACITY]; } }
class Node<K,V>{ private K key; private V value; private Node next; private int hash; Node(){ } Node(K key, V value, Node next, int hash) { this.key = key; this.value = value; this.next = next; this.hash = hash; } public K getKey() { return key; } public void setKey(K key) { this.key = key; } public V getValue() { return value; } public void setValue(V value) { this.value = value; } public Node getNext() { return next; } public void setNext(Node next) { this.next = next; } public int getHash() { return hash; } public void setHash(int hash) { this.hash = hash; } }
而这个数据结构能循环的三个方法,put,get,以及resize;
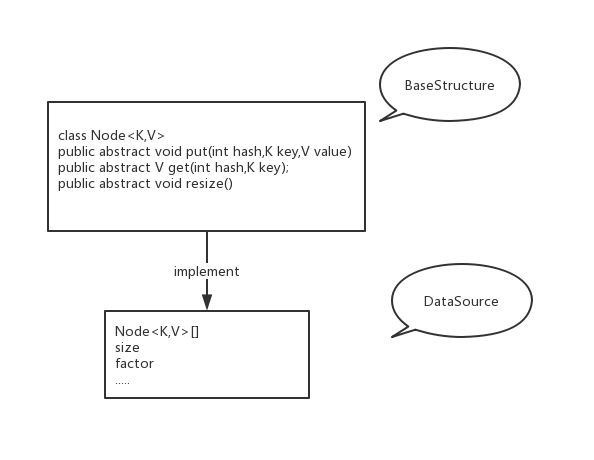
public abstract class BaseStructure<K,V> { class Node<K,V>{ private K key; private V value; private Node next; private int hash; Node(){ } Node(K key, V value, Node next, int hash) { this.key = key; this.value = value; this.next = next; this.hash = hash; } public K getKey() { return key; } public void setKey(K key) { this.key = key; } public V getValue() { return value; } public void setValue(V value) { this.value = value; } public Node getNext() { return next; } public void setNext(Node next) { this.next = next; } public int getHash() { return hash; } public void setHash(int hash) { this.hash = hash; } } public abstract void put(int hash,K key,V value); public abstract V get(int hash,K key); public abstract void resize(); }
以及真正实现的类。
import java.io.Serializable; public class DataStructure<K,V> extends BaseStructure<K,V> implements Serializable { private Node<K,V>[] tab; private final int DEFAULT_CAPACITY = 1 << 2; private double factor = 0.75f; private int size; public DataStructure(){ tab = new Node[DEFAULT_CAPACITY]; } public void put(int hash,K key,V value){ if(key == null){ throw new NullPointerException(); } int len = tab.length; int index; Node e = tab[index = (hash & (len -1))]; // 粗略估计扩容 if(size + 1 > (len * factor)){ resize(); } if(e == null){ tab[index] = new Node(key,value,null,hash); size++; }else{ while(e.getNext() != null) { if (e.getKey().equals(key) && e.getHash() == hash) { e.setValue(value); return; } e = e.getNext(); } e.setNext(new Node(key,value,null,hash)); size++; } } public V get(int hash,K key){ if(key == null){ throw new NullPointerException(); } int len = tab.length; int i = hash & (len -1); Node<K,V> node = tab[hash & (len - 1)]; while(node != null){ if(node.getHash() == hash && node.getKey().equals(key)){ return node.getValue(); } node = node.getNext(); } return null; } @Override public void resize() { int len = tab.length; int newLen = len << 1; Node<K,V>[] newTab = new Node[newLen]; for(int i=0;i<len;i++){ Node<K,V> node = tab[i]; if(node == null){ continue; } else if(node.getNext() == null){ newTab[node.getHash() & (newLen - 1)] = node; }else{ Node<K,V> loHead = null,loTail = null,hiHead = null,hiTail = null; Node<K,V> e = node; Node<K,V> next = null; do{ next = e.getNext(); if((node.getHash() & len) == 0){ if(loHead == null){ loHead = loTail = e; loTail.setNext(null); }else { loTail.setNext(e); loTail = e; loTail.setNext(null); } }else { if(hiHead == null){ hiHead = hiTail = e; hiTail.setNext(null); }else { hiTail.setNext(e); hiTail = e; hiTail.setNext(null); } } }while ((e = next) != null); newTab[i] = loHead; newTab[i+len] = hiHead; } } tab = newTab; } }