《深入浅出统计学》豆知识摘录8～

8连续概率分布--正态分布

离散概率分布只能取 确定值。通过计数得到。

连续数据，则是通过测量得到，比如一根头发的长度。

离散的情况，可以给特定数值一个概率，但连续的情况，则取一个范围的数值来计算概率。 -->概率密度函数。

概率密度函数 f(x)

• 描述连续随机变量的概率分布。
• 概率密度函数是图上的一条线。
• 概率是线下的面积。（可以用微积分求面积）

概率=面积

线下的总面积=1=总概率。

对于连续概率，只能通过概率密度函数f(x)下的面积求出概率。

比如求P(a< X < b)，就必须计算a和b之间的概率密度函数下方的面积。

正态分布： 连续数据的“理想”模型

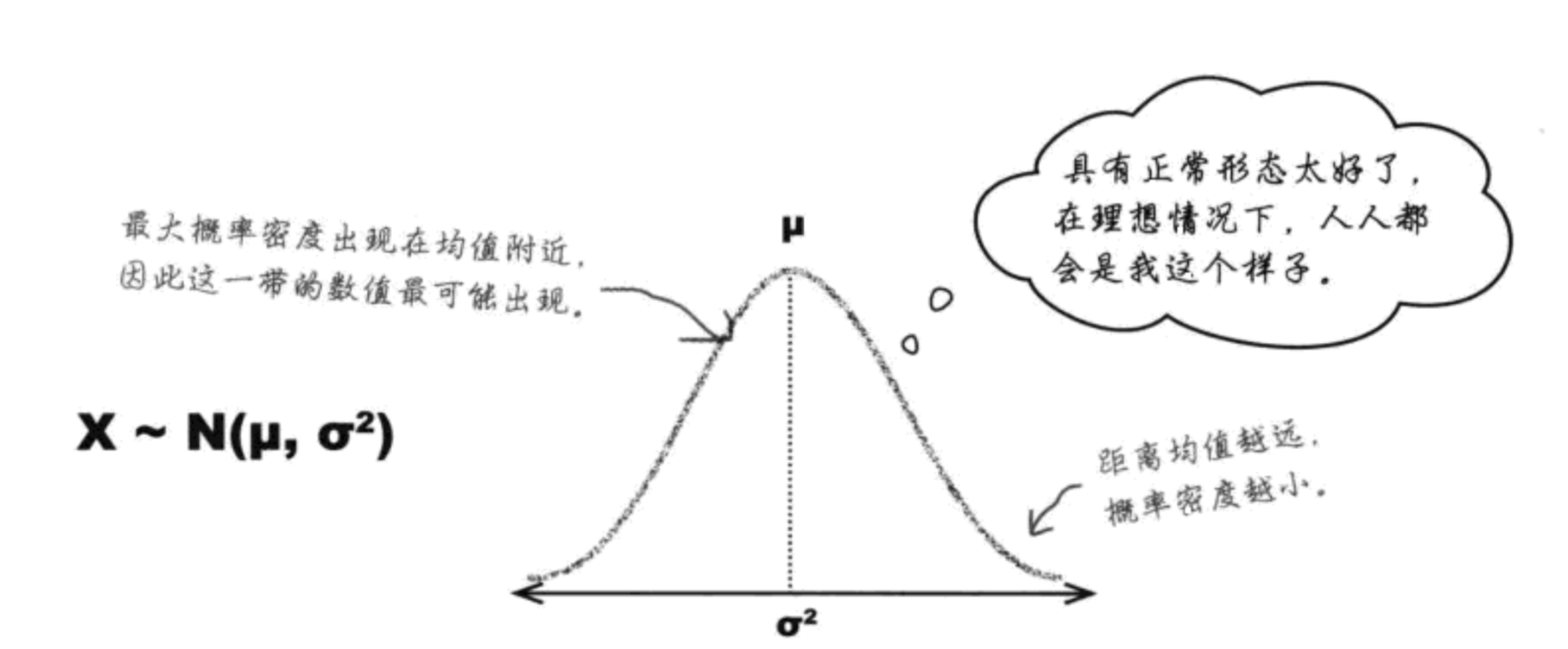
X～N(u, σ²)

查看概率就是查看f(x)下的面积，可以用查询表，或者计算公式，下面是步骤：

1. 确定分布和范围
2. 标准化
3. 查找概率

第二步骤：标准化为X~N(0, 1)

这是因为概率表给出的是N(0,1)的分布的概率。

需要改2个参数u和σ：

1. 移动u
2. 收窄σ²

X~(0,1) 变为  z = (x-u) / σ  ~ N(0, 1)

然后用z值进行查表。

连续概率分布的众数：曲线位置最高处。

中位数将概率密度曲线下面的面积一分为2的数值。

备注

本章有大量练习未做，第九章是关于正太分布的扩展知识。暂时忽略。

---

10统计的抽样

 总体：准备对其进行测量和研究分析的整个群岛。

普查：对总体进行研究/调查。

样本：一部分从总体中选择的对象。

样本的选择非常重要，因为选择的样本必须能够代表总体。

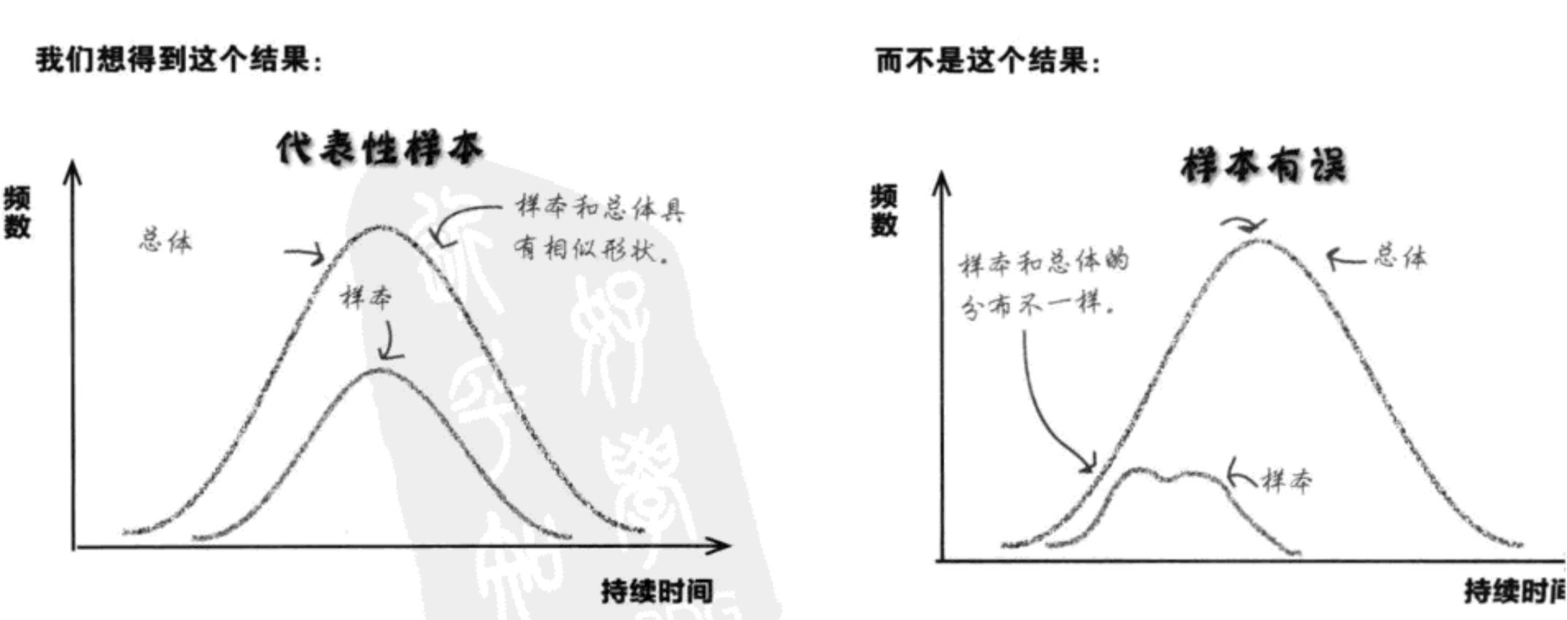
如何设计样本？

1. 确定目标的总体。
2. 确定抽样的单位。
3. 确定抽样空间。包括问题设计要全面。

抽样种类：

1. 简单的随机抽样：包括重复和不重复。方式是抽签或使用随机编号生成器
2. 分层抽样：根据类别分组。每组中的单位特性是类似的。对每组进行简单随机抽样。
3. 整群抽样：分多个群，每个群都和其他群类似。用简单随机抽样抽取几个群，然后这些群中的每一个抽样单位形成样本。
4. 系统抽样：选一个数值k，每经过k个抽样单位就抽一次。

---

11 预测--适用样本估计整体

通过样本了解总体。

• 总体均值u
• 样本均值
• 点估计量：根据样本数据得出的对你认为的总体均值的最佳猜测

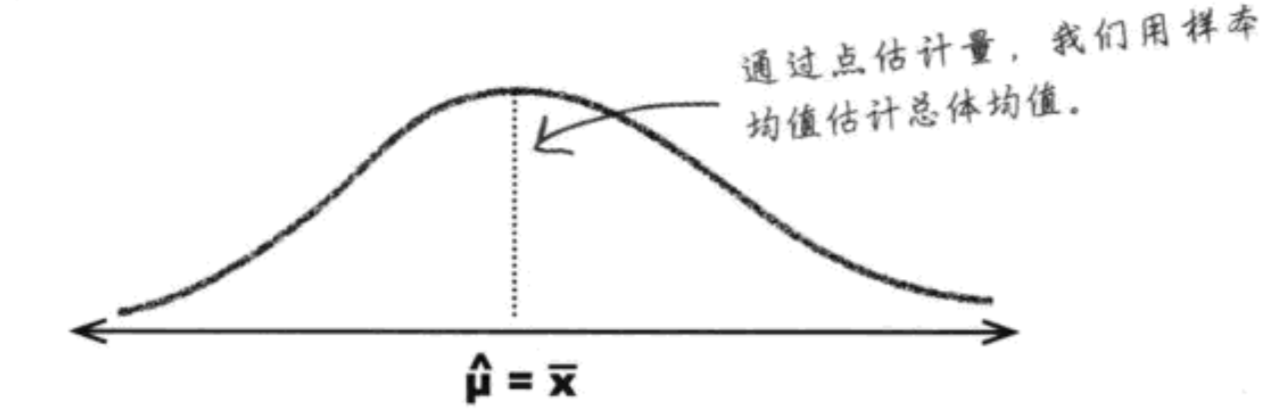
总体方差的点估计量：

这样得到的值比样本数据的真实方差大一点。

因为样本数据本身就少于总体数据，所以用除以n-1得到的方差，更接近总体方差。精确性更好。

概率和比例关系密切

probability = proportion

总体的比例等于样本的比例，适用于二项分布。

总体比例用p, 即总体的成功比例。

P的点估计量为p_s,  是样本的成功比例ṗ = p_s

为样本计算概率--计算在一个整体中出现某一特定比例的概率

1. 查看和特定样本的大小相同的所有样本。
2. 观测所有的样本的比例形成分布，然后求出比例的E(X)和方差。
3. 通过上面得到的比例的分布，求特定样本的概率。

例子：

求一大盒特定的糖球中有40颗或以上是红色的概率。总体上，一大盒糖球中有四种颜色，每种都占1/4。

1， 每个大盒都有100颗糖球。 n = 100。 p = 0.25, X ~ B(100, 0.25)。

• 设置特定样本中的红色糖球数量： X； 则此样本中红色糖球的比例 p_s = X / n

2,  每个样本的Ps都不同，所以其方差E(Ps) = E(X/n) = E(X) / n 。

• X ~ B(100, 0.25), 是二项分布， E(X) = np ,所以 E(Ps) = np /n = p
• 即期望样本的成功比例和总体的成功比例一样。 
• E(Ps) = p

3， 再计算方差： Var(Ps) = Var(X/n),

• Var(ax) = a²Var(X), 本例子，a = 1 / n
• 所以Var(Ps) = Var(X) / n² = pq / n  = p(1-p) / n
• 它的平方根：叫“比例标准误差”

 n越大，比例标准误差越小

4，Ps符合正态分布。Ps ~ N(0.24, 0.001875)

1. 求P(Ps >= 0.4)，首先进行连续性修正。 （这个知识点没有学习，直接给结果）P(Ps >=0.395)
2. 求标准分。z = 0.395 - 0.25 / 0.001875的平方根 = 3.35
3. P(Z >3.35) = 1 - P(Z < 3.35) , 查表得到0.0004.

答案： 一盒100颗的糖球中，红色糖球数量至少是40颗的概率是0.0004。非常小的概率。

什么是抽样分布

从总体中用相同的方法抽取多个大小相同（n）但存在差异的样本，然后用它们共同的属性形成一个分布，所得到的结果就叫做“抽样分布”

所以，用每个样本的比例形成的抽样分布就是“比例的抽样分布”。

通过抽样分布计算，我们可以在已知总体的情况下，计算样本的成功比例的概率。

另一个问题，求样本均值的概率。

已经知道总体均值和方差，求样本均值的概率分布，然后求某个样本均值的概率。

均值的抽样分布

从总体中抽多个大小相同（用n表示大小）的可能样本，计算每个样本的样本均值，用这些样本的均值形成分布，叫做“均值的抽样分布”。 

求任何变量的概率，首先求这个变量的概率分布。

第一步，所有求样本均值的概率分布： 期望和方差 

• E(样本均值) = u, 我们期望样本均值就是总体的均值。 
• Var(样本均值) = σ²/ n
• ⚠️u， σ是总体均值和标准差

第二步，确定样本均值是如何分布的。是否符合正态分布。

• 中心极限定理：

• 如果从非正态总体X抽取一个样本，样本很大，则样本均值的分布接近正态分布 

• 

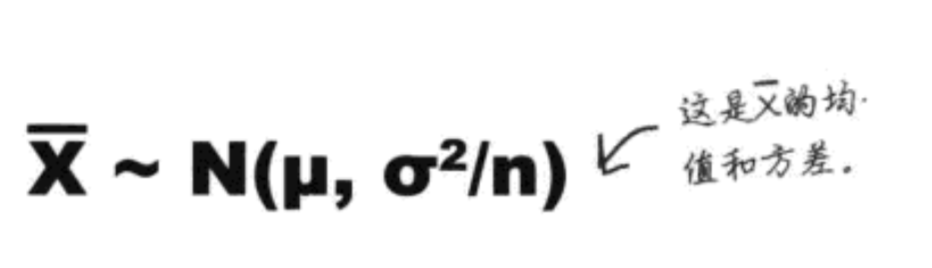
最后一步，通过z = x -u / σ 转化，然后查表即可。

总结：

1. 查看和研究样本大小相同的所有可能样本。
2. 求出样本均值的期望和方差。
3. 只要n>=30, 那么就样本均值符合正态分布。用该分布求概率。

---

12 考虑不确定--置信区间

上一章，提到样本均值，点估计量，方差的点估计量等概念。

点估计量的推导：

• 确保样本无偏差，
• 使样本具有代表性。

但是不能完全代表总体。因为用的是样本。是存在误差的。我们要为误差提供一个区间，即一个误差范围，在这个范围内的误差是允许的。

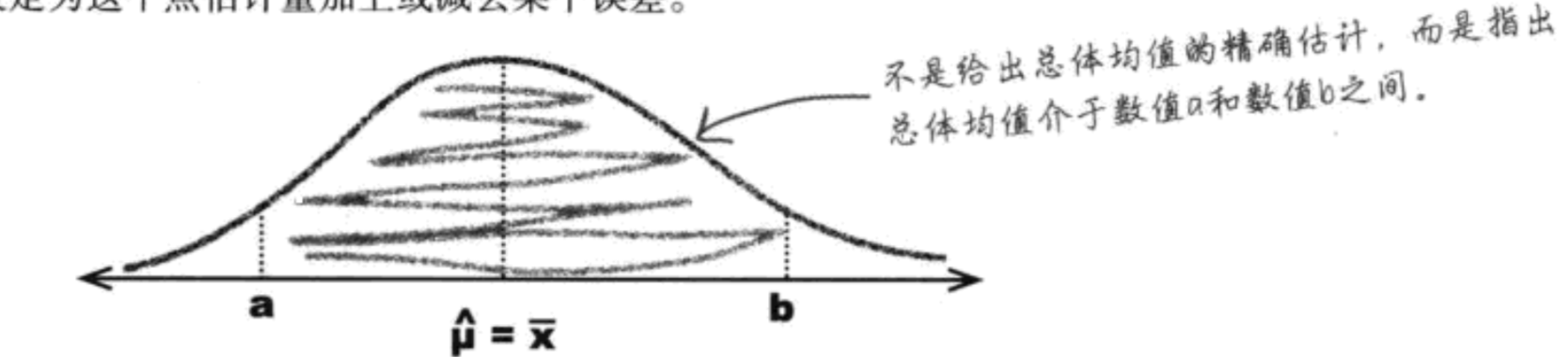
置信区间 (a,b)

 

 P(a<u<b) = 0.95  ，即置信水平是95%。上下限a,b

 

求解置信区间：

 总体均值，总体比例都是统计计量的一种。

例子：

第一步：在本书实例中，选择总体均值u来构建置信区间，

第二步：E(样本均值) = u ,  Var(样本均值) = σ²/ n

因为不知道总体方差σ²的值，使用总体方差的点估计代替，用上一章公式求得。

求得样本均值～N(u,  σ²/ n)

第三步，确定置信水平，一般用 P(a<u<b) = 0.95。

第四步，求a,b.上下限， 根据面积的对称性：求 P(x < a) = 0.0025和P(x > b) = 0.0025

• 求z值 = x -u / σ²
• Z ~ N(0,1)
• 用概率表得到: Za，Zb = |1.96|

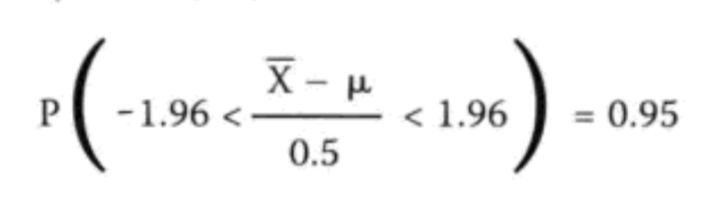
通过计算最后求得a和b。

已经求得u的95%的置信区间（a,b）, 意味着从总体中抽取100个样本，其中有95个样本的样本均值位于a,b之间。

 

本书504页提供了简便的查公式算置信区间的方法。

 

本章还有一个特殊的T分布，用于不知道总体方差，同时样本很小的情况。

---