统计概率--概率分布

统计概率--概率分布

probability:一个事件发生的可能性的数值度量。

数据挖掘很重要的概念。

⚠️讲概率，谈的都是可能性，不谈确定性。

01概率--试验计数

概念

• 试验： 产生明确结果的过程。单一的重复试验中，只有一个试验结果。
• 样本空间： 一个试验的所有可能结果的集合。
• 样本点： 一个试验的结果，样本空间的一个元素。
• 事件及其概率：
  • 事件是样本点的一个集合
  • 事件（发生）的概率等于事件中所有样本点的概率之和。

例子：

试验：

样本空间：8，9，10，9，10，11，10，11，12

样本点：共计9个。

事件：比如10，10，10这个三个样本点的样本相同，算作一类事件x。

事件发生的概率：事件x的发生概率就是3/9

计数法则，排列和组合（高中课本的知识）

多步骤试验：

一个试验分为连续的k个步骤，每个步骤有n种可能的结果，所有试验结果的个数：n1*n2...*nk.

组合：

从N个物品的集合中，随机拿出n个。

N！= N*(N-1)*(N-2)*....*2*1

n!  = n* (n-1)(n-2)*...*2*1

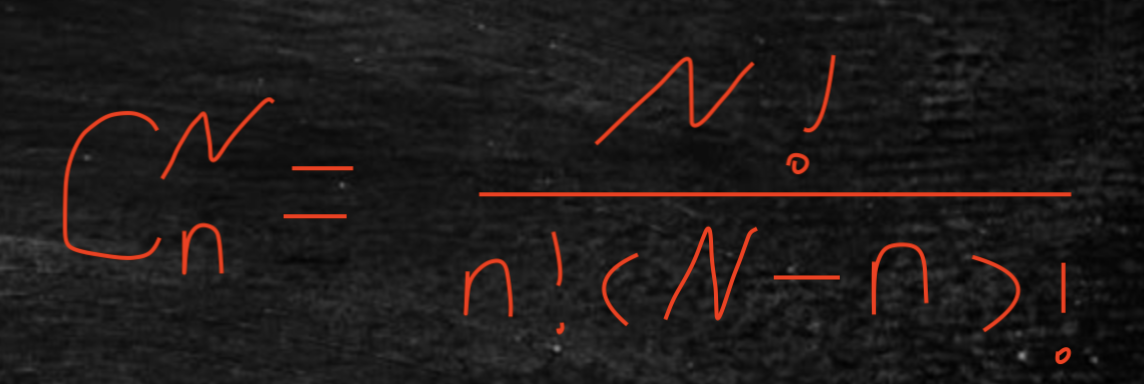
排列 permutations，

• 从N个物体的集合中选取n个物体，考虑排序。
• 去掉n!
• 更好理解，第一次从N拿个，第二次从N-1里拿，拿n次。N*(N-1)*(N-2)*...*N-(n-1)

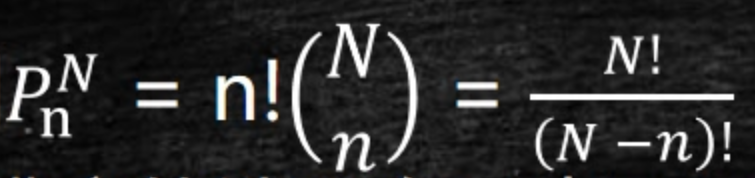
概率的基本性质

事件的补（集）： 一个事件A, 事件A的补是指：由所有不属于事件A的样本点组成的事件。

 P(A) + P(A^c) = 1 ⚠️它们共同构成了样本空间。

加法公式： p(AUB) = P(A) + P(B) - P(A∩B)   ⚠️∩是交集， U是并集。

互斥事件： 事件A和B之间没有共同的样本点。 p(AUB) = P(A) + P(B)  

---

02条件概率  P(A|B)

贝叶斯定理用到了条件概率。

联合概率： 两个事件的交的概率。

事件A发生的可能性经常会受到另一个相关事件发生与否的影响。此时事件A发生的可能性叫条件概率， 记作P(A|B)

• P(A|B) =P(A∩B) / P(B)
• 事件B发生后，事件A也发生的概率。即： 联合概率 / 概率B。 

例子：

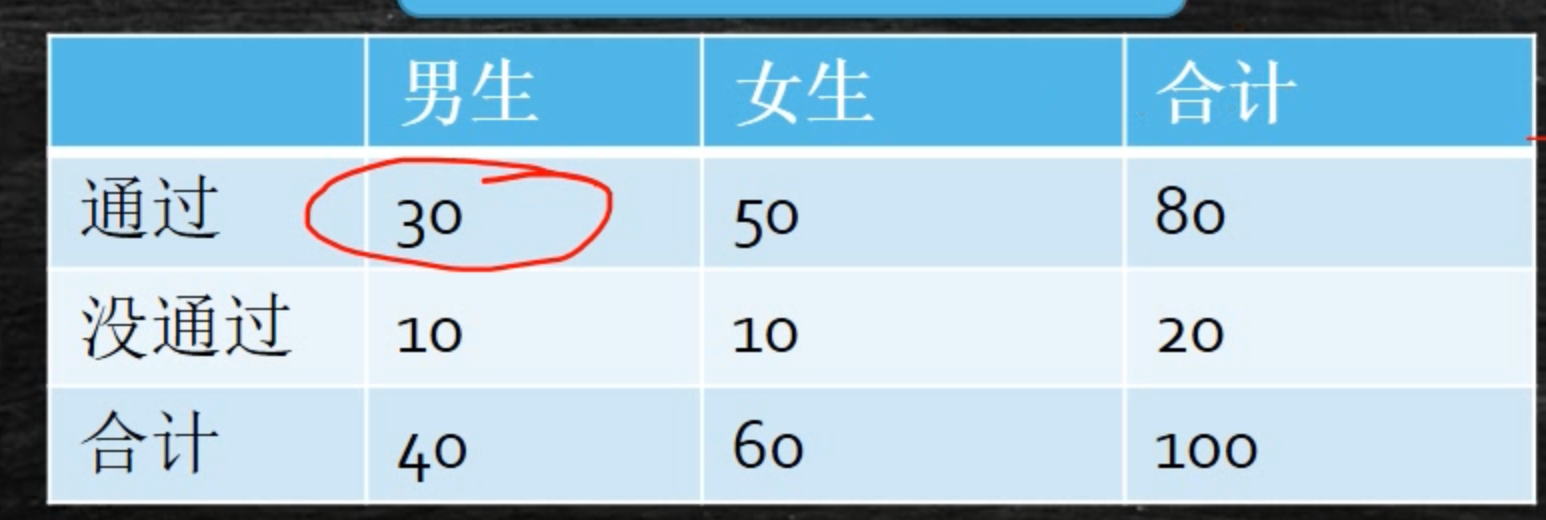
由图可知： 

1.  样本空间： 100个学生。
2.  样本点： 每个学生。
3. 事件： {"男生"：40个， "女生":60个}。
4. 事件： {"通过": 80个,    "没通过"：20个}。
5.  事件男生∩事件通过--样本点：30个。因此P(男生∩通过)= 30 /100 = 30%   --联合概率
6. 条件概率：P(男生|通过) = 0.3/0.8 = 0.375。
   • 白话解释：通过的人中，男生占百分之多少：37.5%。
   • P(通过|男生)的意思则是：  男生中，有百分之多少是通过的。 0.3/0.4 = 75%

独立事件（不存在条件）

• P(A|B) = P(A) 
• 事件B是否发生，不影响事件A发生的概率。即事件A发生的可能性不受事件B的影响。
•  乘法公式（且是独立事件）：
  • P(A∩B)= P(A)*P(B)=P(A)*P(B|A)=P(B)*P(A|B) 
    
  • 用来计算两个事件交的概率。
• 乘法公式（不一定是独立事件）：
  • P(A∩B)= P(A)*P(B)
    

独立事件是一个假设，比如有1000样本的空间，假设这1000个样本互相独立，互不影响。

---

03贝叶斯（数据挖掘中会用：朴素贝叶斯）

特定事件X给出一个初始的概率，也叫先验概率，即通过历史经验得到的概率。

从样本，试验中得到了有关该事件X的补充信息，根据这些信息计算修正概率， 得到后验概率

例子：https://www.cnblogs.com/chentianwei/p/12488891.html 

  

P(A1|B) = P(A1∩B)         /       P(B)

          = P(A1∩B)          /       [P(A1∩B) + P(A2∩B)]  

          =  P(A1)*P(B|A1)   /      [P(A1)*P(B|A1) + P(A2)*P(B|A2)]

• (利用了乘法公式。分母是全概率)
• 第一行， 条件概率公式
• 第二行， 分母用到事件的补集的公式。 
• 第三行， 用到独立事件的乘法公式。 形成一个贝叶斯公式。

要求倒背如流！！！ 

---

04 离散型概率分布

随机变量：对一个试验结果的数值描述

离散变量和连续变量

离散变量是指其数值只能用自然数或整数单位计算的则为离散变量.例如,企业个数,职工人数,设备台数等,只能按计量单位数计数,这种变量的数值一般用计数方法取得.

反之,在一定区间内可以任意取值的变量叫连续变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值.例如,生产零件的规格尺寸,人体测量的身高,体重,胸围等为连续变量,其数值只能用测量或计量的方法取得.

离散随机变量和连续随机变量

随机变量并不是变量，它们实际上是将（样本空间中的）结果映射到真值的函数。我们通常用一个大写字母来表示随机变量。

概率函数f(x) 

例子：

骰子有6个样本点。每个样本点的出现概率都是1/6，因此也叫做离散均匀随机变量概率

x范围是：1~6。

f(x) = 1/6

∑f(x) = 1

随机变量的数学期望和方差

随机变量的数学期望(Expected value)/均值是对随机变量中心位置的一种度量。

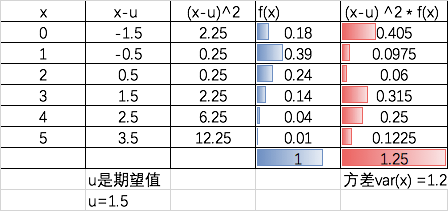
• 离散型随机变量的数学期望  E(X) = ∑ x*f(x)  

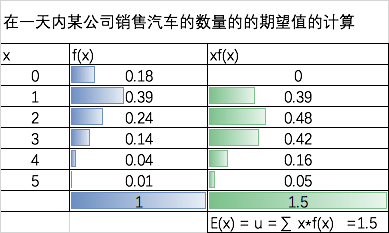
⚠️，这一天，实际卖出的汽车数量，可能是0，也可能是1-5种的任意数字。

本例的期望是1.5，即从长期看，未来每天会卖1.5辆车，即平均每天卖1.5辆车。

方差

方差描述随机变量的变异性： Var(x) =  ∑(x-u) ² f(x)  ⚠️此处是u代表期望值

---

二项概率分布

Binomial distribution 二项分布

二项分布（英语：Binomial distribution）是n个独立的是/非试验中成功的次数的离散概率分布

⚠️每个试验也叫0-1试验（伯努利试验）

在现实世界里应用广泛，来源即基于著名的贝努利试验。

当一个物理量只有两种属性，如：合格/不合格，超标/不超标等都会符合二项分布。

二项试验：

1. 由一系列相同的n个试验组成。
2. 每次试验由2种可能的结果，其中一种表示成功，另一种失败
3. 每次试验成功的概率都相同，用p表示； 失败的概率也相同， 1-p表示。
4. 试验是相互独立的。
5. 当n = 1时，二项分布就是伯努利分布

如抛硬币，就是二项试验。

如掷一颗骰子，把掷出数字6表示成功，那么其他数字都算是失败。

二项概率函数f(x)

• f(x)代表n次试验，有x次成功的概率。
• x代表成功的次数。
• p代表一次试验成功概率

⚠️: execl有二项分布概率函数：BINOMDIST

 

例子1：抛硬币，6次，6次有3次是成功的概率是多少？

答案：f(3) = 0.5³*0.5³ * 组合COMBIN(6,3)  = 20/64 =31.25%

分析：

1.  成功0.5*0.5*0.5
2.  失败0.5*0.5*0.5
3. 因为，不在乎抛硬币的成功顺序，所以是组合，需要乘以组合6次试验有3次成功。6！/ [3！*（6-3）！]  = 20

推导公式：

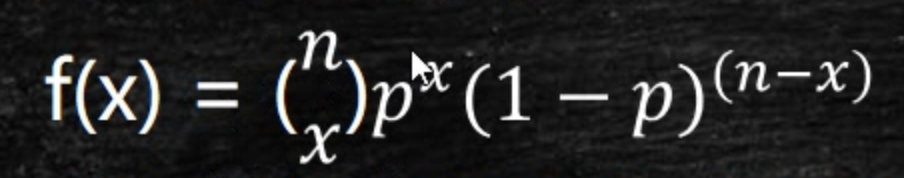
 x个成功概率相乘，再乘以(n-x)个失败概率。因为不在乎顺序，所以乘以组合。

伯努利分布（0-1分布）

一种离散概率分布。

• 试验成功，随机变量取值：1， 成功概率为
• 试验失败，随机变量取值：0

E(x) = ∑ x*f(x)  = 1*p+ 0*(1-p) = p

var(x) = (0-p)²(1-p) + (1-p)²p = p(1-p)

 

二项分布的数学期望E和方差Var(x)

二项试验就是n伯努利试验，所以E和方差是：

• E(x) = np
• var(x) = np(1-p) 

思路：遇到问题，先考虑二项分布。

---

泊松分布

描述单位时间内随机事件发生的次数的概率分布。也是一个常见的离散型分布。

关于柏松，相关内容很多，这里只讲柏松分布的公式和用法。

描述在特定时间段或空间段中，事件发生的次数，需要满足以下2个条件：

• 在任意两个等长的区间上，事件发生的概率相同。
• 在任意1个区间，是否发生事情和其他区间是否发生无关，独立的。

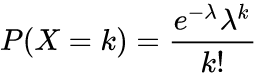 （来自wiki）

 泊松分布的参数λ是单位时间（或单位面积）内随机事件的平均发生率。即数学期望。

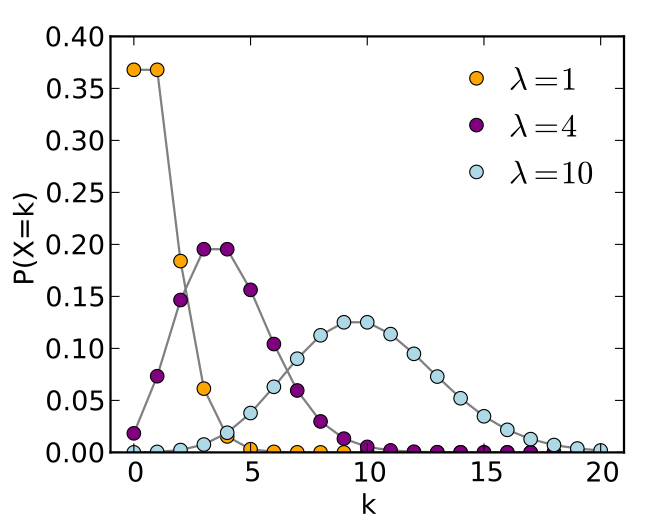
 横轴是索引k，发生次数。该函数只定义在k为整数的时候。连接线是只为了指导视觉。

 当参数λ=10，k是0～20，各自的概率p，组合成正态分布。

• 单位时间内平均发生概率是10次，10次算一个事件，这个事件发生的概率，图上显示接近0.15.
• 发生9/11次, 这两个事件发生的概率，也接近0.125

---

超几何概率分布

离散概率分布的一种。

注意：各个试验不是独立的，各个试验中成功的概率不相等。

---

05 连续性概率分布

对于离散型随机变量，概率函数f(x)给出了随机变量x的取某个值的概率。

对于连续随机变量，变量可以无限分隔，基于这个特点，概率函数对应->概率密度函数

• 给定的区间上曲线f(x)下的面积，给出连续随机变量在该区间取值的概率。

均匀概率分布

 p(120=< x =< 140) = 1/20 

正态概率分布

描述连续型随机变量的最重要的一种概率分布。

1. 均值，标准差会影响数据分布
2. 标准差决定曲线的宽度，平坦程度，越小图越陡峭。
3. 对称的图
4. 正太分布曲线的总面积是1。
5. 正态随机变量的概率->由面积决定。 

均值u。

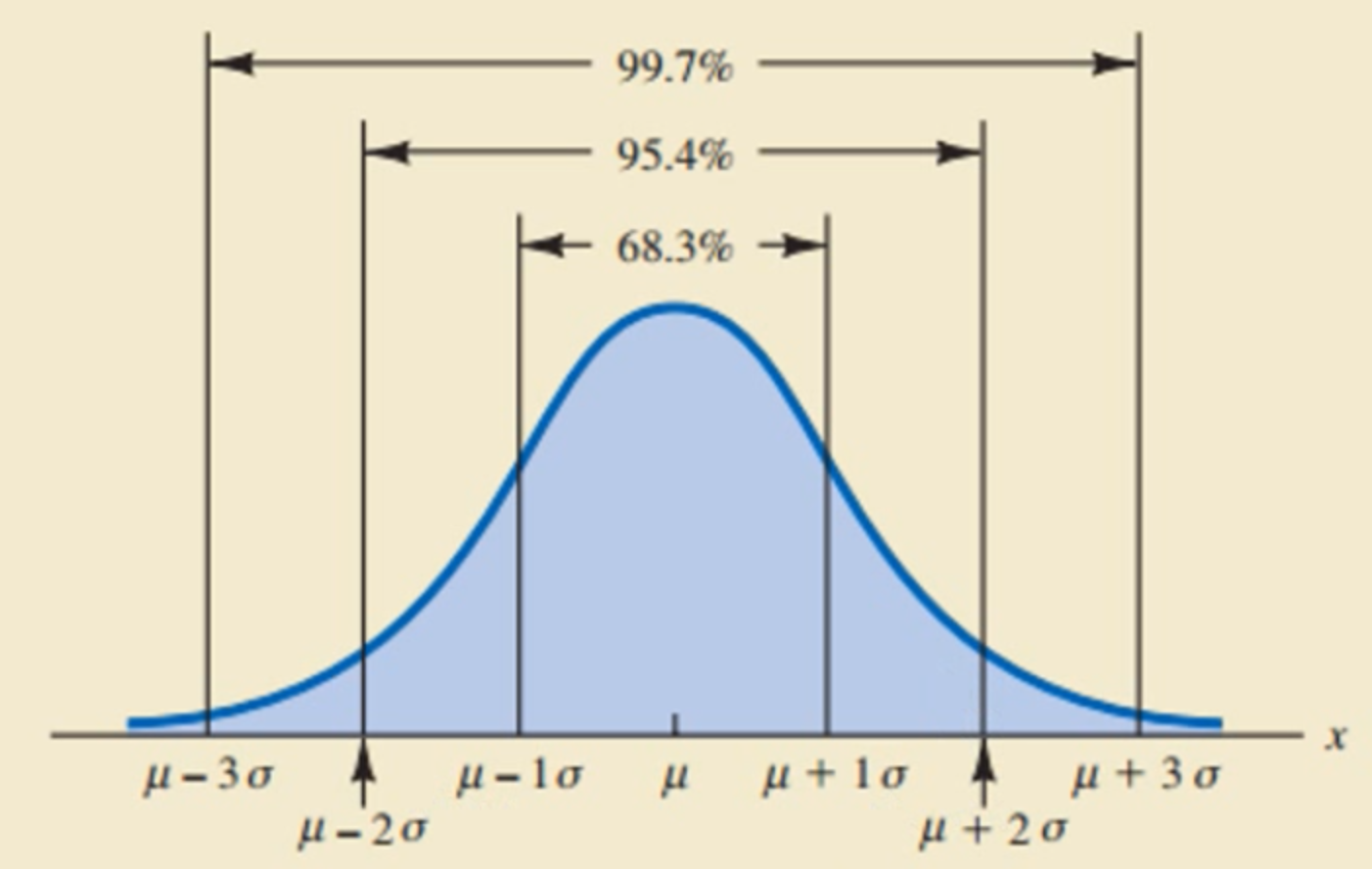
标准正态概率分布

正态随机变量服从均值u=0， 标准差为1的正态分布

查表计算某一 范围的正态随机变量。

• 表格中的数据都是左侧的面积
• 利用标准正态分布的对称性，可以进行p(y<=z<=x)的范围运算。
  •  标准正态随机变量z<=一个给定值的概率
  • z在两个给定值之间的概率
  • z>=一个给定值的概率

  

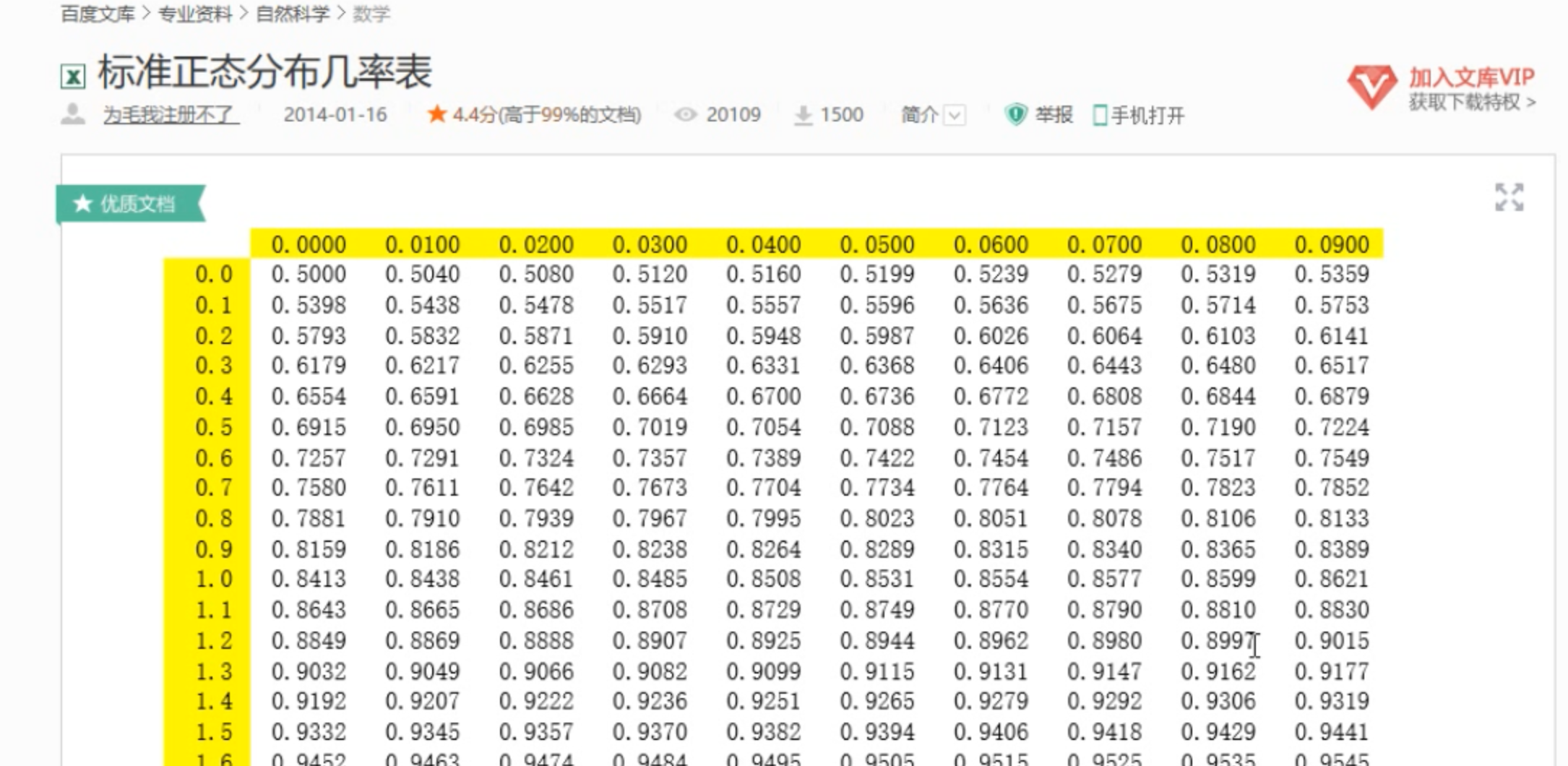
普通的正态分布可以通过公式转换为标准正态分布。z = (x-u)/标准差

z是正态随机变量。

例子：