昨日同学要我帮他看一道算法,如下:
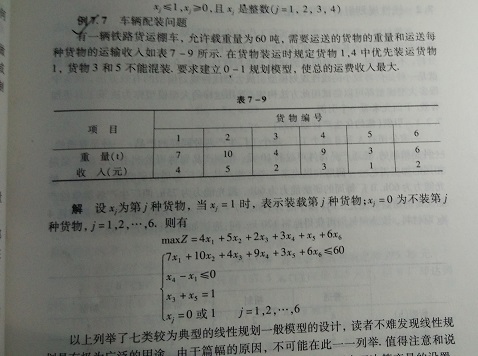
是不是乍一看是“0-1背包”问题呀,我也这么想,于是就这么兴致勃勃的开始用这个想法去思考怎么算。但是算法也忘得差不多,回去赶紧补补,也趁着这次机会好好复习一下算法,于是觉得“0-1背包”问题实现了,这个问题也差不多了吧:
/***********************0-1背包*************************************/
1 //先将那两个条件忽略,单纯利用动态规划 -------------------这里就看出有多傻-—_-- 2 //利用动态规划求解 3 #include <iostream> 4 #define MAX_NUM 50 5 #define MAX_WEIGHT 100 6 using namespace std; 7 8 //动态规划求解 9 int zero_one_pack(int total_weight, int w[], int v[], int flag[], int n) { 10 int c[MAX_NUM + 1][MAX_WEIGHT + 1] = { 0 }; //c[i][j]表示前i个物体放入容量为j的背包获得的最大价值 11 // c[i][j] = max{c[i-1][j], c[i-1][j-w[i]]+v[i]} 12 //第i件物品要么放,要么不放 13 //如果第i件物品不放的话,就相当于求前i-1件物体放入容量为j的背包获得的最大价值 14 //如果第i件物品放进去的话,就相当于求前i-1件物体放入容量为j-w[i]的背包获得的最大价值 15 for (int i = 1; i <= n; i++) { 16 for (int j = 1; j <= total_weight; j++) { 17 if (w[i] > j ) { 18 // 说明第i件物品大于背包的重量,放不进去 19 c[i][j] = c[i - 1][j]; 20 } 21 22 else { 23 //说明第i件物品的重量小于背包的重量,所以可以选择第i件物品放还是不放 24 if (c[i - 1][j] > v[i] + c[i - 1][j - w[i]]) { 25 c[i][j] = c[i - 1][j]; 26 } 27 else { 28 c[i][j] = v[i] + c[i - 1][j - w[i]]; 29 } 30 } 31 } 32 } 33 34 //下面求解哪个物品应该放进背包 35 int i = n, j = total_weight; 36 while (c[i][j] != 0) { 37 if (c[i - 1][j - w[i]] + v[i] == c[i][j]) { 38 // 如果第i个物体在背包,那么显然去掉这个物品之后,前面i-1个物体在重量为j-w[i]的背包下价值是最大的 39 flag[i] = 1; 40 j -= w[i]; 41 } 42 --i; 43 } 44 return c[n][total_weight]; 45 } 46 47 //回溯法求解 48 49 int main() { 50 int total_weight = 60; 51 int w[7] = { 0,7, 10, 4, 9, 3,6 }; 52 int v[7] = { 0,4, 5, 2, 3, 1 ,2}; 53 int flag[7]; //flag[i][j]表示在容量为j的时候是否将第i件物品放入背包 54 int total_value = zero_one_pack(total_weight, w, v, flag, 6); 55 cout << "需要放入的物品如下" << endl; 56 for (int i = 1; i <= 6; i++) { 57 if (flag[i] == 1) 58 cout << i << "重量为" << w[i] << ", 价值为" << v[i] << endl; 59 } 60 cout << "总的价值为: " << total_value << endl; 61 system("pause"); 62 return 0; 63 }
查看一下结果,
卧槽,瞎了。背包值这么大原来!于是乎还是想着如何利用“0-1背包”解决,但越想越不对劲,要让程序记住所有路径然后根据条件进行筛选,发现是在太过于复杂。但什么算法可以呢,于是想到了N皇后问题,介于设置的最大载重量太大,不具代表性,于是大大减少最大载重量,设计一下,行表示要存放的对象,列用1,0表示是否要放入,利用不断的回溯递归取得所有可能的值,再选择最大值:
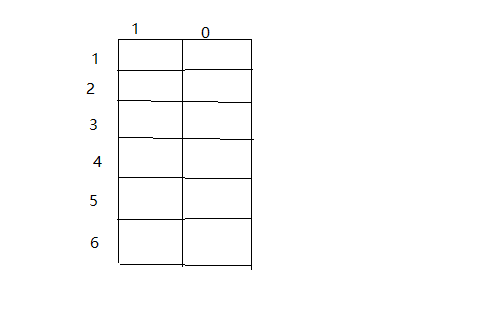
/***********************N皇后*****************************************/
1 #include <iostream> 2 using namespace std; 3 4 int total_weight = 35; //修改最大值 5 int w[7] = { 0, 7, 10, 4, 9, 3, 6 }; 6 int v[7] = { 0, 4, 5, 2, 3, 1, 2 }; 7 int result[7] = { 0 }; 8 int result_all[10][7] ;//用于存储所有的可能结果 9 int indi = 0; //结果指针 10 int num = 6; 11 12 13 int sumV(); 14 int sumW(int n); 15 16 //判断下一个是否符合条件 17 bool judge(int n) 18 { 19 if (n == 4) 20 { 21 if (result[4] >= result[1]) 22 return true; 23 else 24 return false; 25 26 } 27 if (n == 5) 28 { 29 if ((result[5] + result[3]) == 1) 30 return true; 31 else 32 return false; 33 } 34 35 if (sumW(n) > total_weight) 36 return false; 37 return true; 38 } 39 40 //主要的递归调用函数 41 void backtrack(int n) 42 { 43 if (n > num) 44 45 { 46 47 for (int i = 1; i <= num; i++) 48 { 49 result_all[indi][i] = result[i]; 50 } 51 indi++; 52 } 53 54 else 55 { 56 for (int i = 1; i >= 0; i--) 57 { 58 result[n] = i; 59 if (judge(n)) 60 backtrack(n+1); 61 } 62 } 63 } 64 65 //计算综价值 66 int sumV( ) 67 { 68 int m = 0; 69 for (int i = 1; i <= num; i++) 70 { 71 if (result[i] == 1) 72 m += v[i]; 73 } 74 return m; 75 } 76 //计算重量 77 int sumW(int n) 78 { 79 int m = 0; 80 for (int i = 1; i <= n; i++) 81 { 82 if (result[i] == 1) 83 m += w[i]; 84 } 85 return m; 86 } 87 88 int main() 89 { 90 backtrack(1); 91 92 //计算最大值 93 int most = 0; 94 int pos = 0; 95 for (int i = 0; i < indi; i++) 96 { 97 int temp = 0; 98 for (int j = 1; j <= num; j++) 99 { 100 if (result_all[i][j] == 1) 101 temp += v[j]; 102 } 103 if (temp>most) 104 { 105 most = temp; 106 pos = i; 107 108 } 109 } 110 111 cout << "最大值是:"<<most<<endl; 112 cout << "结果是:" << endl; 113 for (int i = 1; i <= num; i++) 114 { 115 cout << result_all[pos][i]<<" "; 116 } 117 cout << endl; 118 system("pause"); 119 }
结果:
所以说啊,算法死记硬背是没啥用的,还得看具体情况来,算法还得多学,这次教训大了。