题目描述
Tammy has a circle. There are 2*n (0<n<=300) points on the circle. She wants to join every pair points using lines without crossing. But how many kinds of method can she get? The graph below indicate one kind of method Tammy can get when n=3.
输入
There are multiple test cases in the input data. In the First Line there is an Integer T(1<=T<=1000), which means the number of test cases in the input. Each of the next T lines contains an Integer n(0<n<=300), which means the number n in that case.
输出
The number of methods Tammy can get. One line per case.
样例输入
3 1 2 6
样例输出
1 2 132
这个题的意思是在一个圆上有2n个点,你要用两两部相交的线将每两个连在一起,问有多少种连法
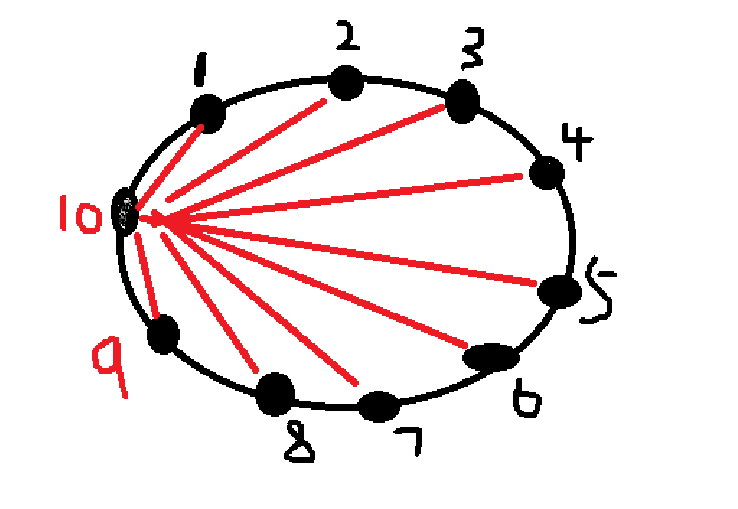
如图,当增加9和10这两个点是,就可以分很多种情况,分别是10与1,3,5,7,9连,当与2连的时候,就分成了0个点与8个点的情况,对应于n==0与4的情况
故这样一看f[5]=f[0]*f[4]+f[1]*f[3]+f[2]*f[2]+f[3]*f[1]+f[4]*f[0];
于此我们得到dp的状态转移方程,f[n]=∑f[i]*f[n-i-1];
初始化为f[0]=f[1]=1;
下面是代码
#include <iostream> #include <cstdio> #include <cstring> #define MOD 100 using namespace std; class BigInt{ public: int v[512],L; BigInt(){ memset(v,0,sizeof(v)); L=1; adjust(); } BigInt(int x){ memset(v,0,sizeof(v)); v[0]=x; L=0; adjust(); } //大数的加法 void add(const BigInt &T){ int i; if (L<T.L) L=T.L; for (i=0;i<L;i++) v[i]+=T.v[i]; adjust(); } //大数的乘法 void mul(const BigInt &T){ int i,j; BigInt Y(0); for (i=0;i<T.L;i++) for (j=0;j<L;j++){ Y.v[i+j]+=T.v[i]*v[j]; } *this=Y; L=L+T.L; adjust(); } void adjust(){ int i; for (i=0;i<L;i++){ v[i+1]+=v[i]/MOD; v[i]%=MOD; } //向前进位 while (v[L]){ v[L+1]+=v[L]/MOD; v[L]%=MOD; L++; } } void display(){ int i; printf("%d",v[L-1]); for (i=L-2;i>=0;i--) printf("%02d",v[i]);//保持2个0 printf(" "); } }; BigInt B[320],T; int N; int main(){ //freopen("in.txt","r",stdin); int i,j,N; B[0]=*(new BigInt(1));//带参数的初始化 B[1]=*(new BigInt(1)); for (i=2;i<301;i++){ for (j=0;j<i;j++){ T=B[j]; T.mul(B[i-j-1]);//B[j]*B[i-j-1] B[i].add(T);//B[i]+T } } scanf("%d",&N); while (N--){ scanf("%d",&i); B[i].display(); } //fclose(stdin); return 0; }