84. 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
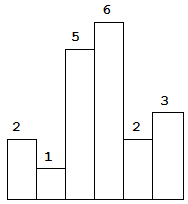
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
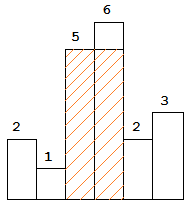
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
解题思路
方法一:暴力
枚举左右边界的方法。先枚举左边界, 然后从左边界开始, 枚举右边界, 在枚举右边界过程记录左右边界之间的最小的高度。然后在所有的枚举边界之内找到最大的值即可。
时间复杂度:O(N^2)
空间复杂度:O(1)
public int largestRectangleArea1(int[] heights) {
int n = heights.length;
int ans = 0;
// 枚举左边界
for (int left = 0; left < n; ++left) {
int minHeight = Integer.MAX_VALUE;
// 枚举右边界
for (int right = left; right < n; ++right) {
// 找到left至right这一段的最小的高度
minHeight = Math.min(minHeight, heights[right]);
// 计算面积
ans = Math.max(ans, (right - left + 1) * minHeight);
}
}
return ans;
}
枚举所有的高度, 然后在此高度向左右延伸, 知道遇到比当前高度小的柱子就停止延伸。
public int largestRectangleArea(int[] heights) {
int n = heights.length;
int ans = 0;
for (int mid = 0; mid < n; ++mid) {
// 枚举高
int height = heights[mid];
int left = mid, right = mid;
// 确定左右边界, 左右边界的值恰好大于等于当前高度
while (left - 1 >= 0 && heights[left - 1] >= height) {
--left;
}
while (right + 1 < n && heights[right + 1] >= height) {
++right;
}
// 计算面积
ans = Math.max(ans, (right - left + 1) * height);
}
return ans;
}
方法二: 单调栈
方法一向左右延伸的方法实际上可以使用单调栈实现。向左右延伸就是要找到比当前高度低的第一个高度。借助一个递增单调栈即可。在当前高度进栈时, 将栈内比当前高度高的元素全部出栈, 那么栈顶元素就是比当前高度低的第一个高度。就这样就找到当前高度的左边界。
同理用这种方法可以找到当前高度的右边界。
时间复杂度:O(N)
空间复杂度:O(N)
public int largestRectangleArea3(int[] heights) {
ArrayDeque<Integer> stack = new ArrayDeque<>();
int[] left = new int[heights.length];
int[] right = new int[heights.length];
// 先通过单调栈找所有高度的左边界
for (int i = 0; i < heights.length; i++) {
while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
stack.pop();
}
left[i] = (stack.isEmpty()) ? -1 : stack.peek();
stack.push(i);
}
stack.clear();
// 再通过单调栈找所有高度的右边界
for (int i = heights.length - 1; i >= 0; i--) {
while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
stack.pop();
}
right[i] = (stack.isEmpty()) ? heights.length : stack.peek();
stack.push(i);
}
// 根据左右边界, 找到最大的面积
int area = 0;
for (int i = 0; i < heights.length; i++) {
area = Math.max(area, (right[i] - left[i] - 1) * heights[i]);
}
return area;
}
其实在通过单调栈找左边界的时候, 右边界也同时找到了。
就是在栈内的元素出栈时, 代表栈内的元素比当前的高度大。反过来的意思是, 当前元素是要出栈的那个元素的右边的第一个元素。所以在出栈的过程, 可以找到所有出栈元素的右边界, 就是当前i。
而最后遍历完, 栈中还保留着的元素的右边界就是N。因为栈内元素右边已经没有比它小的元素了。
public int largestRectangleArea(int[] heights) {
ArrayDeque<Integer> stack = new ArrayDeque<>();
int[] left = new int[heights.length];
int[] right = new int[heights.length];
Arrays.fill(right, heights.length);
// 通过单调栈找到当前高度的左边界
for (int i = 0; i < heights.length; i++) {
while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
// 将出栈元素的右边界设置为当前位置
right[stack.pop()] = i;
}
left[i] = (stack.isEmpty()) ? -1 : stack.peek();
stack.push(i);
}
stack.clear();
// // 根据左右边界, 找到最大的面积
int area = 0;
for (int i = 0; i < heights.length; i++) {
area = Math.max(area, (right[i] - left[i] - 1) * heights[i]);
}
return area;
}