题目描述:
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
要完成的函数:
vector<vector<int>> subsets(vector<int>& nums)
说明:
1、这道题给定一组不重复的元素,要求返回这组元素所有可能的子集,也就是返回幂集。
每个可能的子集存储在一维vector中,所有的子集合起来存储在二维的vector中。
2、举个例子,给定的vector是[1,2,3,4]。
那我们人类在做这道题的时候,都是想:
0个元素的:[]
1个元素的:1 2 3 4
2个元素的:12 13 14 23 24 34
3个元素的:123 124 234
4个元素的:1234
2个元素的子集,是在1个元素的子集的基础上形成的。
比如1可以扩散出12 13 14,2可以扩散出23 24……
这像是树开枝散叶,往外扩散的样子?
我们这样子看:
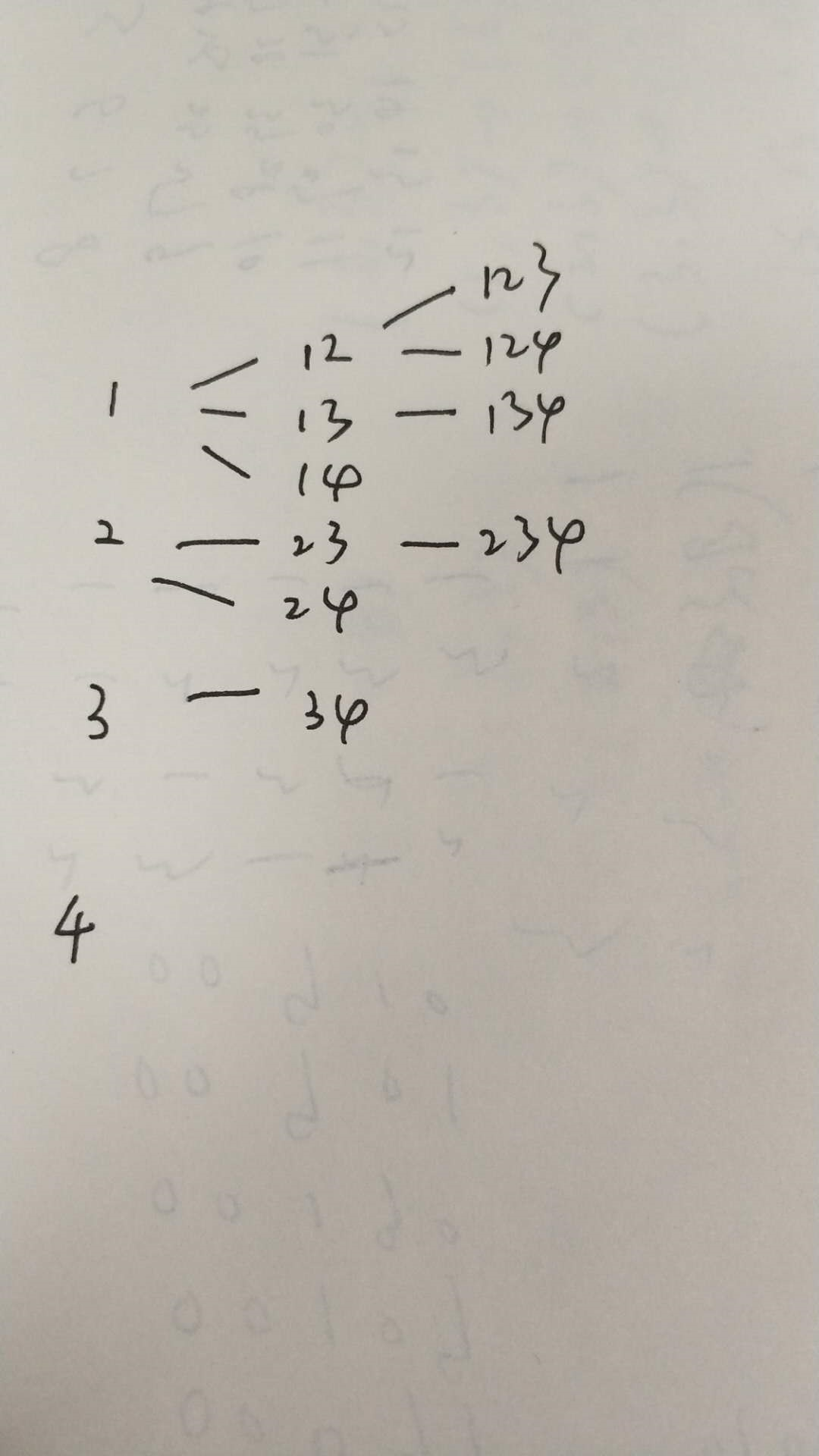
我们其实最后要的是宽度优先搜索这棵树的结果。
所以这道题其实是一道BFS(宽度优先搜索)的题目,用熟悉的队列就可以解决。
代码如下:(附详解)
void bfs(vector<vector<int>>& res,queue<vector<int>>& q,int s1,vector<int>& nums)
{//这里要带上&,指针,传参数快,而且在存储空间中修改了res的值,最后也能在subsets函数中得到
int i,count=1;
while(!q.empty())//当存储中间过程的数据不空
{
for(int j:q.front())//把第一个vector中的坐标数据读出来,插入到res[count]中,最开始是[0]
res[count].push_back(nums[j]);
count++;
i=q.front().back();//得到最后一个坐标,i=0
while(i+1<s1)
{
q.push(q.front());在q的末尾插入[0]
q.back().push_back(i+1);//在q的最后一个vector,也就是刚刚插入的[0],再插入1,形成[0,1]
i++;//i++,不断循环
}
q.pop();//去掉第一个vector,最开始时是[0]
}
}
vector<vector<int>> subsets(vector<int>& nums)
{
int s1=nums.size();
vector<vector<int>>res(pow(2,s1),vector<int>{});//提前申请好2^s1个vector<int>空间
queue<vector<int>>q;//我们用队列来存储中间过程的数据
for(int i=0;i<s1;i++)//如果给定nums是[1,2,3],那么这里存储它们的坐标[0],[1],[2]
q.push({i});
bfs(res,q,s1,nums);//带着res的指针和q的指针以及nums这些数据,进入bfs函数
return res;//返回最终的res
}
上述代码其实就是bfs的实现过程,只不过我们没有真的去建树,直接把数据插入到队列中。
上述代码实测4ms,beats 100.00% of cpp submissions。