之前在讨论 RNN (递归神经网络) 的梯度消失 和 梯度爆炸都会对咱的网络结构产生极大的影响.
梯度爆炸, 也是在参数更新这块, 调整步伐太大, 产生 NaN 或 Inf, 代码就搞崩了直解决梯度消失...而对于梯度爆炸而已, 可以采用 clipping 的方式, 对向量进行缩放, 而不改变其方向.
梯度消失, BP的参数训练, 求导的链式法则, 可能会有项直接乘积非常小, 整个式子没有梯度, 表 词间的关联性弱. 而那篇中呢, 其实是特意留了一个待解决的方案没有去说明. 其实就是为了引出今天要谈的 LSTM.
Fix vanishing gradient
The main problem is that it is too difficult for the RNN to learn to preserve (保存) information over many timesteps (传统的 RNN 中, 没有对 每个状态的信息进行保存)
In a vanilla RNN, the hidden state is constantly being rewritten (状态更新, 就覆盖掉原来的状态信息)
(h^{(t)} = sigma(W_hh^{(t-1)} + W_xx^{(t)} + b))
看这公式就能明白, t 时刻的输出, 是由 (t-1) 时刻的 输入得到的.... 也就是说, 随着状态的不断改变, h(t) 也在不断地 插除和改写自己.
We think that how about a RNN with separate memory (另外给整个地方, 单独存起来). 那这种思路呢, 就是咱今天说的 LSTM (Long Short Term memory)
LSTM
A type of RNN proposed by Hochreiter and Schmidhuber in 1997 as a solution to the vanishing gradients problem. 两个德国的大兄弟提出来的, 针对梯度消失这块.
On step t, there is a hidden state (h^{(t)}) and a cell state (c^{(t)})
- Both are vectors length n (隐含层, 产生这两个向量)
- The cell stores long-term infomation 就是用另外一个向量, 去记录每个时刻的信息. (差不多这个意思)
- The LSTM can erase, write and read information from the cell. (能从这个 cell 中, 去读取, 改写相应的信息)
The selection of which information is erased / read / writen is controlled by three corresponding gates
- The gates are also vectors length n .(每个门也是长度为 n 的向量)
- On each timestep, each element of the gates can be opend(1), closed(0) 或者是 (0~1) 之间的值.
- The gates are dynamic : their values is computed based on the current context. (基于上下文来改变 gates 值的变化的)
用公式来表达的就是这样的形式.

当然, 如果还是不够详细的话, 可以再用更为形象一点的图来表示哦
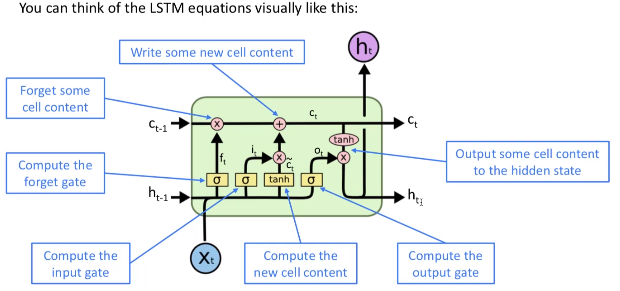
Why LSTM can solve vanishing
The LSTM architecture makes it easier for the RNN to preserve information over many timesteps (保留早期的状态信息)
这也是 LSTM 最为关键的一点 与 传统的 RNN 即保留了早期的状态信息呀.
But, LSTM does not guarantee that there is no vanishing. 也没有能做到完全避免, but it does provide an easier way for the model to learn long-distance dependencies. 在在实践应用中还是满成功的, 从几年来看的话. 行了. LSTM 就先到这里吧, 只要在理解 RNN 的基础上, 掌握它这里的一个 状态保留动态的状态 (达到保留早期信息的方式来尽可能解决梯度消失) . 即可.