Last we learned Recurrent Neural Netwoks (RNN) and why they'er great for Language Modeling (LM) 就之前整理 RNN 作为语言模型的神经网络, 理解上还是可以, 关键点在于 W 的复用, 和 上一个状态的输出, 作为下一状态的输入. 如果对语言模型也稍微了解的话, 对于 RNN 就能很自然过渡, 网络的逻辑, 也并不复杂.
这里呢就想来讨论下, 最基础的 RNN 所待解决的问题, 比如标题所谈的梯度消失, 或者梯度爆炸. 然后如何去 fix them. 然后再引入一些 More complex RNN variants (其他的 RNN 变体 如 LSTM, GRU) 等, RNN 我感觉在应用上, 还是蛮不错的.
然后呢就是关于Vanishing Gradient Problem (梯度消失) 从而引出 LSTM 和 GRU ... 还有各种变体, 如 Bidirectional -RNN; Multi - layer - RNN...
梯度消失与爆炸
这是神经网络都可能会存在问题, 因为训练大多基于BP 算法的, 从数学上看就是 多元函数求偏导, 以及求导过程中应用链式法则. 中间就是很多项相乘嘛, 如果都是 非常小的数相乘, 那整个结果就接近 0 了呀, 没有梯度了.
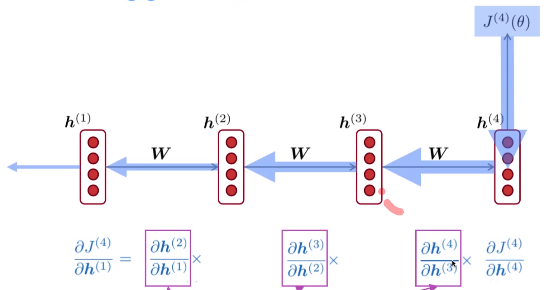
就像这张图所表示的那样, 如果中间的项很小...那整体的结果, 就造成了梯度消失的问题 (Vanishing gradient) .
Vanishing gradient proof sketch
直接从隐含层来看出端倪.
(h^{(t)} = sigma(W_hh^{(t-1)} + W_xx^{(t)} + b_t ))
隐含层取决于, 给定的输入 x 先onehot 在 embedding, 再和复用的权值矩阵 W 相乘 and 上一个时间点的 W_h 和 h 的乘积. 再作为激活函数的输入. 最后到一个值都在[0, 1] 之间的向量.
然后对 (h^{(t-1)}) 来求导 (链式法则哦)
$frac {partial h^{(t)} {1}} {partial h^{(t-1)}} = $ (diag (sigma ' (W_hh^{(t-1)} + W_xx^{(t)} + b_t ) )W_h)
- 链式法则而已. 相当于是 y = h(z), z = ax; 要求 y 对 x 的偏导, 即: h(z)' * 偏z 对 偏 x 的值 ....
- 对于 sigmoid 函数(简记 (sigma(x)) 求导的结果是, (sigma(x) [1-sigma(x)])
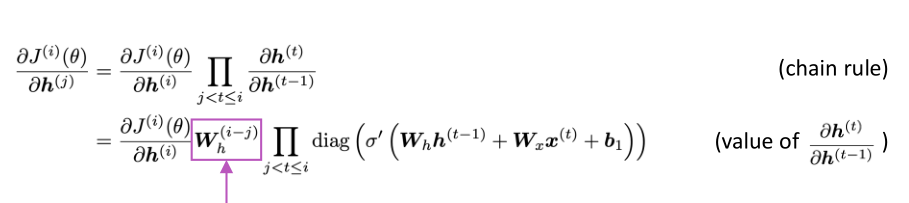
这个 latex 写得让人头疼... 贴个图算了, 尤其是这种复杂的上下标啥的.
当 (W_h) 非常小的时候, 它的 (i-j) 次方, 这个值就会变得非常小了呀. 注意 W_h 是个矩阵啥. 我们通过说的 矩阵的小, 指其 模 非常小 (|W_h|) 或者是说, 对这个矩阵 进行 特征分解 (eigenvalue, eigenvector) , 它最大的特征值 的绝对值 如果最大的特征值, 小于 1 则 (||W_h||) 这个行列式的值会变很小. (前人已经证明了, 我也没懂, 就先记一个结论来用着) 如果最大的特征值大于1, 则可能会带来梯度爆炸的问题 (exploding gradients).
Why is vanishing gradient a problem
解释一: 从导数的意义上.
梯度消失的表现, 如下图表示的那样, 回归到 导数的意义, 用来衡量 "变化率" (frac {dy} {dt})
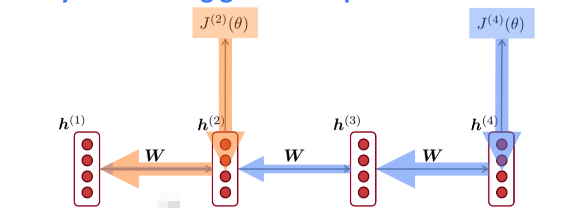
出现梯度为零, 则表示, 对于 h 的一个微小增量, 而 j 并未受到啥影响. 从图上来看, 就是隔得太远, 如 j(4) 基本不会受到 h(1) 的影响了呗. 或者详细一点可以这样说:
Gradient signal from faraway is lost because it's much smaller than gradient signal from close-by
So model weights are only updated only with respect to near effects, not long-term effects.
**解释二: **
Gradient can be viewed ans measure (测量) of the effect of the past on the future. 字面意思就是, 梯度, 可以看成是, 未来对现在的衡量. 梯度小, 则表示未来对现在的影响小.
未来影响现在?? 我感觉这个时间线, 似乎不太理解哦
总之哈, 梯度很小所反映的基本事实是:
- 在第 t step 和 t + n step , 如果 n 比较大, 则 这两个状态的 单词的 "关联度" 比较小
- 因而我们所计算出来的参数就不正确了哦.
Why is exploding gradient a problem
同样的, 梯度爆炸, 也是一个大问题. (从用梯度下降法来更新参数, 能能直观看出)
If the gradient becomes too big, then the SGD (随机梯度下降法) update step become too big.
( heta^{new} = heta^{old} - alpha abla _ heta J( heta))
这一块, 基本了解 ML 的都贼熟悉哈. 本质上是对参数向量的一个调整嘛, 当梯度 ( abla _ heta J( heta)) 特别大的时候, 然后整个参数被都这波节奏给带崩了.
This can cause bad updates : we take too large a step and reach a bad paramenter configuration (with large loss)
从代码运行角度看,
In the worst case (更加糟糕的是) , this will result in inf or NaN in your network. Then you have to restart training from an earlier checkpoint. 就是代码报错, 要重写搞, 一重写运行, 几个小时又过去了...这也是我不太想学深度学习的原因之一.
解决 - 梯度消失和爆炸
solve vanishing
先 pass 下
solve exploding
有种方法叫做, Gradient clipping: If the norm of the gradient is greater than some threshhold (阀值), scale it down before applying SGD update.
如下图所示, 对参数向量 g 取模, 如果它大于某个阀值, 就 将其更新为 (下图) 相当于对 g 进行了一个缩放 (变小了)

向量缩放的特点是, 没有改变其原来的方向, SGD 中, 就还是沿着 梯度方向来调整参数 哦.
即, take a step in the same direction, but a small step. 有点东西哦.
小结
- 熟练 RNN 的网络结构和特性, 如 W 复用, 输出 -> 输入
- 梯度消失, BP的参数训练, 求导的链式法则, 可能会有项直接乘积非常小, 整个式子没有梯度, 表 词间的关联性弱
- 梯度爆炸, 也是在参数更新这块, 调整步伐太大, 产生 NaN 或 Inf, 代码就搞崩了直接
- 解决梯度消失...
- 解决梯度爆炸, 可以采用 clipping 的方式, 对向量进行缩放, 而不改变其方向.