基础概念
二叉树(binary tree)是一棵树,其中每个结点都不能有多于两个儿子。
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
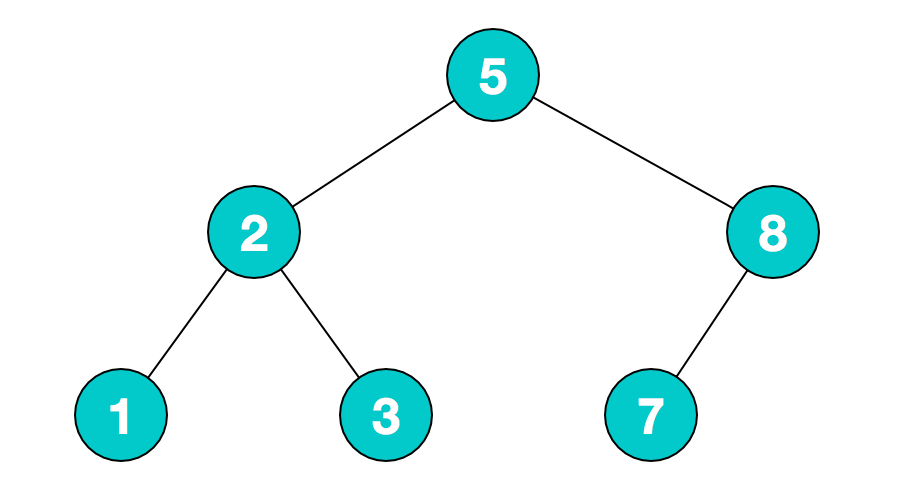
二叉树的遍历
二叉树的遍历是指从根节点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。二叉树的遍历方式有很多,主要有前序遍历,中序遍历,后序遍历。
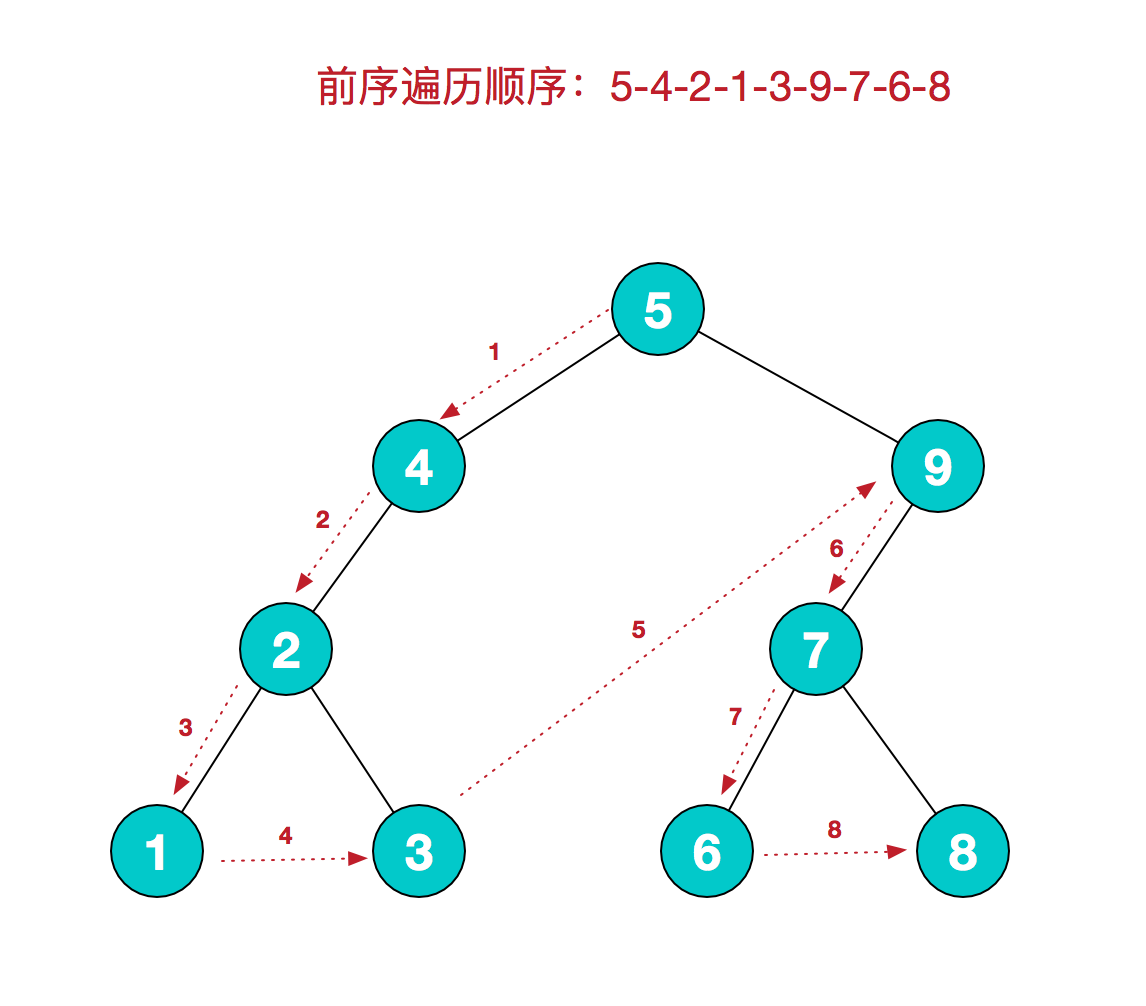
前序遍历
前序遍历的规则是:若二叉树为空,则空操作返回,否则先访问根节点,然后前序遍历左子树,再前序遍历右子树
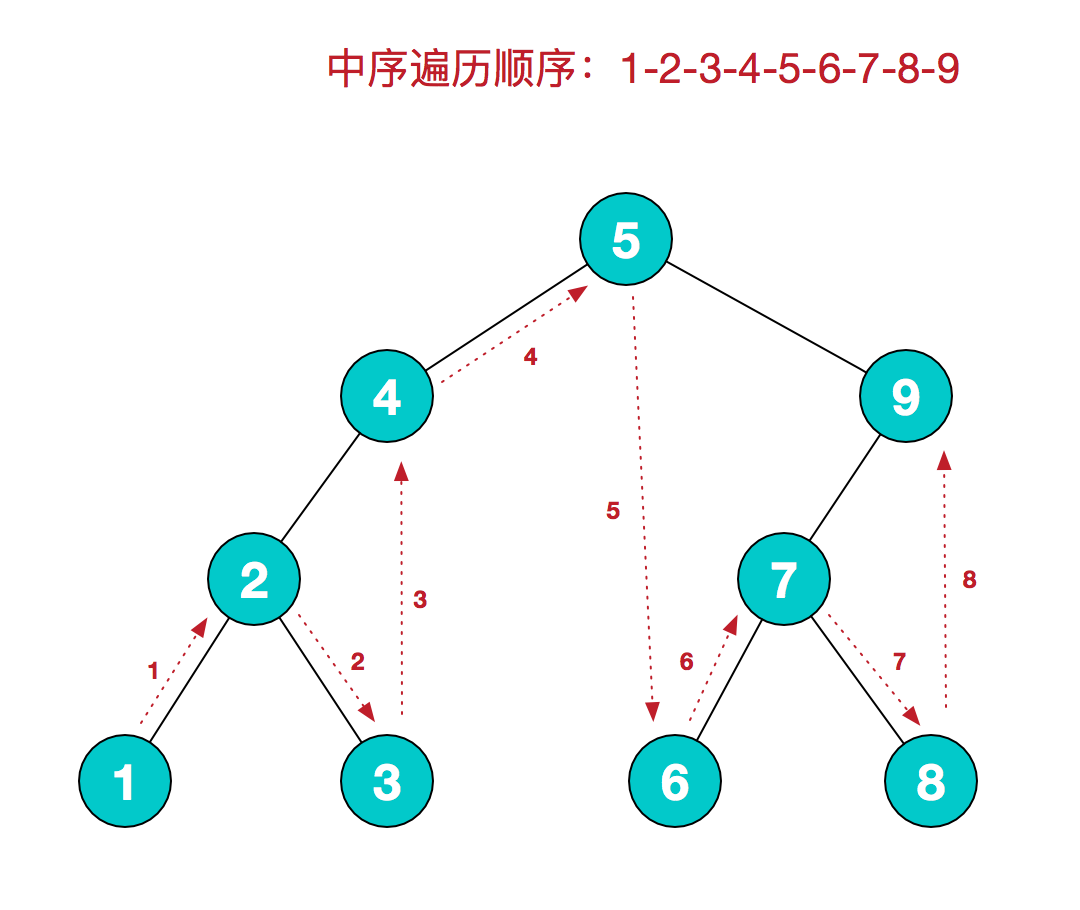
中序遍历
中序遍历的规则是:若树为空,则空操作返回;否则从根节点开始(注意并不是先访问根节点),中序遍历根节点的左子树,然后是访问根节点,最后中序遍历右子树。可以看到,如果是二叉排序树,中序遍历的结果就是个有序序列。
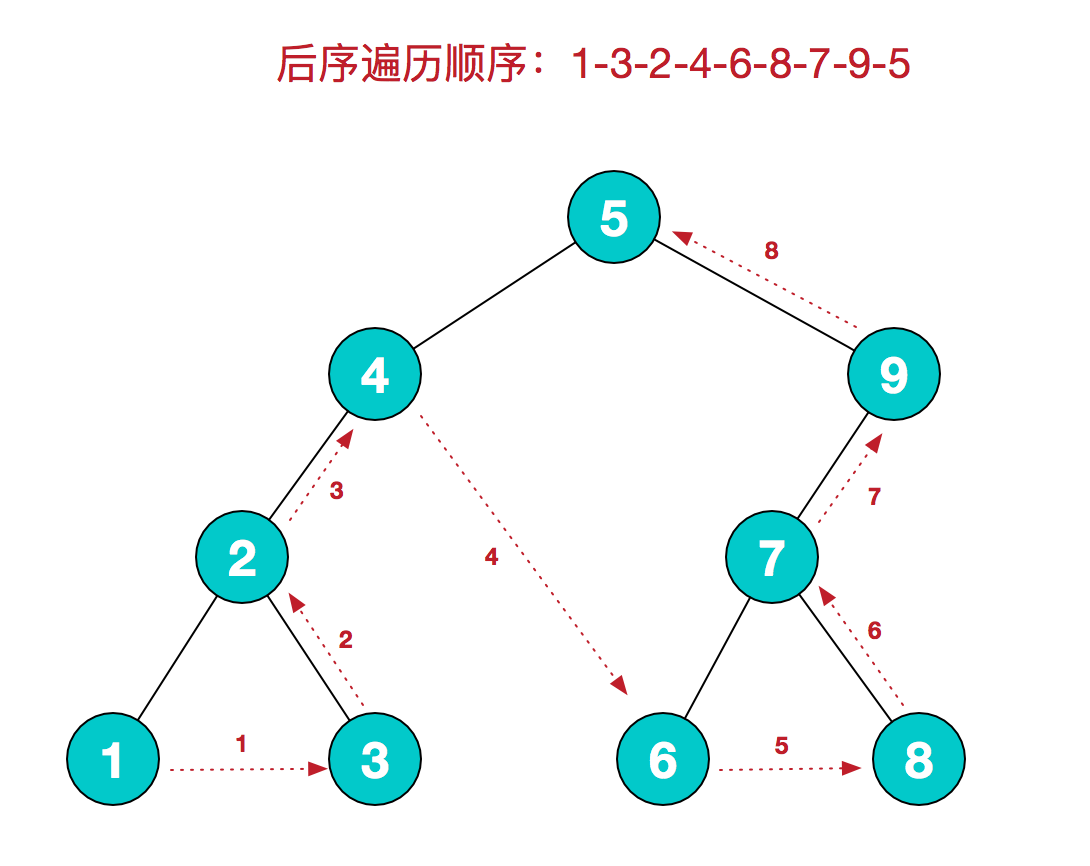
后序遍历
后序遍历的规则是:若树为空,则空操作返回;然后先遍历左子树,再遍历右子树,最后访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。
删除结点
对于二叉排序树的其他操作,比如插入,遍历等,比较容易理解;而删除操作相对复杂些。对于要删除的结点,有以下三种情况:
1.叶子结点;
2.仅有左子树或右子树的结点;
3.左右子树都有结点;
对于1(要删除结点为叶子结点)直接删除,即直接解除父节点的引用即可,对于第2种情况(要删除的结点仅有一个儿子),只需用子结点替换掉父节点即可;而对于要删除的结点有两个儿子的情况,比较常用处理逻辑为,在其子树中找寻一个结点来替换,而这个结点我们成为中序后继结点。
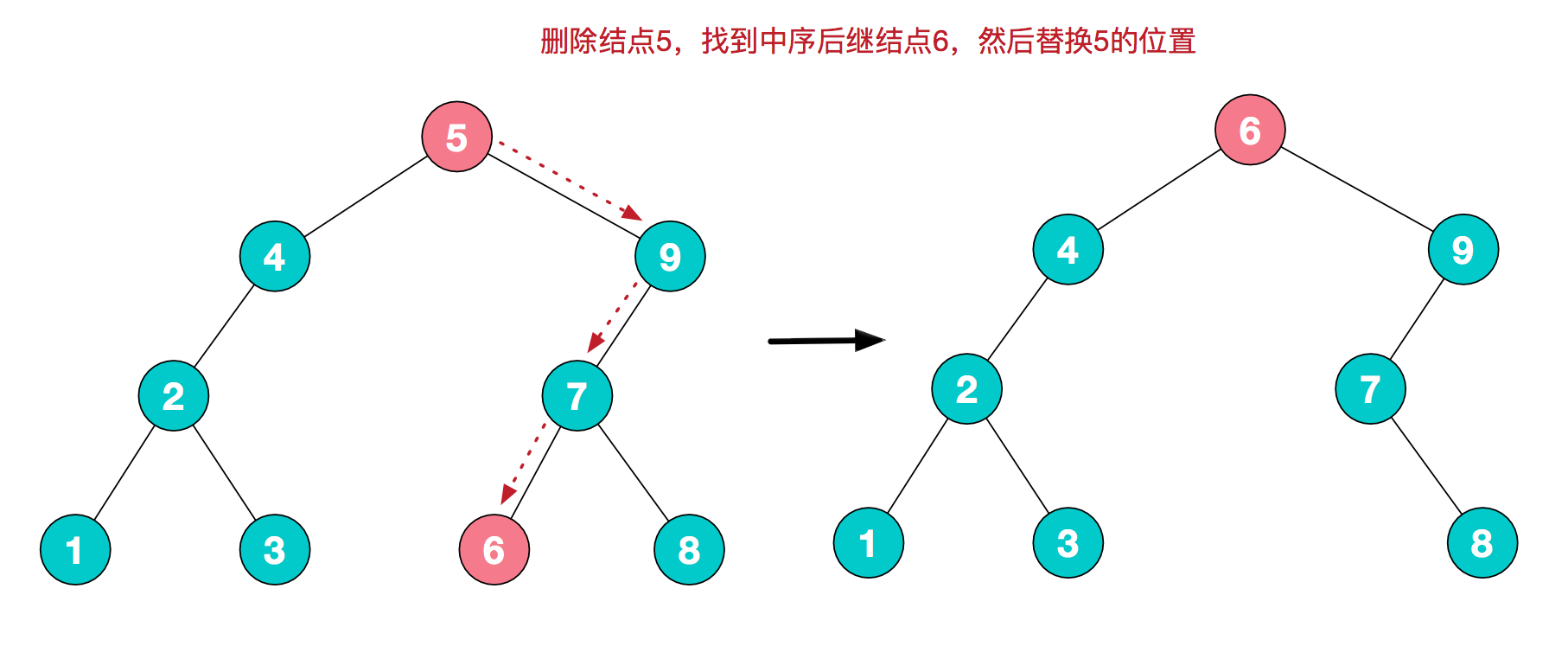
可以看到,我们找到的这个用来替换的结点,可以是删除结点的右子树的最小结点(6),也可以是其左子树的最大结点(4),这样可以保证替换后树的整体结构不用发生变化。为什么称为中序后继结点呢?我们来看下这棵树的中序遍历结果 1-2-3-4-5-6-7-8-9。可以很清晰的看到,其实要找的这个结点,可以是结点5的前驱或者后继。
代码实现

1 package treeDemo;
2
3 /**
4 * Created by chengxiao on 2017/02/12.
5 */
6 public class BinaryTree {
7 //根节点
8 private Node root;
9 /**
10 * 树的结点
11 */
12 private static class Node{
13 //数据域
14 private long data;
15 //左子结点
16 private Node leftChild;
17 //右子结点
18 private Node rightChild;
19 Node(long data){
20 this.data = data;
21 }
22 }
23
24 /**
25 * 插入结点
26 * @param data
27 */
28 public void insert(long data){
29 Node newNode = new Node(data);
30 Node currNode = root;
31 Node parentNode;
32 //如果是空树
33 if(root == null){
34 root = newNode;
35 return;
36 }
37 while(true){
38 parentNode = currNode;
39 //向右搜寻
40 if(data > currNode.data){
41 currNode = currNode.rightChild;
42 if(currNode == null){
43 parentNode.rightChild = newNode;
44 return;
45 }
46 }else{
47 //向左搜寻
48 currNode = currNode.leftChild;
49 if(currNode == null){
50 parentNode.leftChild = newNode;
51 return;
52 }
53 }
54 }
55
56 }
57
58 /**
59 * 前序遍历
60 * @param currNode
61 */
62 public void preOrder(Node currNode){
63 if(currNode == null){
64 return;
65 }
66 System.out.print(currNode.data+" ");
67 preOrder(currNode.leftChild);
68 preOrder(currNode.rightChild);
69 }
70
71 /**
72 * 中序遍历
73 * @param currNode
74 */
75 public void inOrder(Node currNode){
76 if(currNode == null){
77 return;
78 }
79 inOrder(currNode.leftChild);
80 System.out.print(currNode.data+" ");
81 inOrder(currNode.rightChild);
82
83 }
84
85 /**
86 * 后序遍历
87 * @param currNode
88 */
89 public void postOrder(Node currNode){
90 if(currNode == null){
91 return;
92 }
93 postOrder(currNode.leftChild);
94 postOrder(currNode.rightChild);
95 System.out.print(currNode.data+" ");
96 }
97
98 /**
99 * 查找结点
100 * @param data
101 * @return
102 */
103 public Node find(long data){
104 Node currNode = root;
105 while(currNode!=null){
106 if(data>currNode.data){
107 currNode = currNode.rightChild;
108 }else if(data<currNode.data){
109 currNode = currNode.leftChild;
110 }else{
111 return currNode;
112 }
113 }
114 return null;
115 }
116
117 /**
118 * 删除结点 分为3种情况
119 * 1.叶子结点
120 * 2.该节点有一个子节点
121 * 3.该节点有二个子节点
122 * @param data
123 */
124 public boolean delete(long data) throws Exception {
125 Node curr = root;
126 //保持一个父节点的引用
127 Node parent = curr;
128 //删除结点是左子结点还是右子结点,
129 boolean isLeft = true;
130 while(curr != null && curr.data!=data){
131 parent = curr;
132 if(data > curr.data){
133 curr = curr.rightChild;
134 isLeft = false;
135 }else{
136 curr = curr.leftChild;
137 isLeft = true;
138 }
139 }
140 if(curr==null){
141 throw new Exception("要删除的结点不存在");
142 }
143 //第一种情况,要删除的结点为叶子结点
144 if(curr.leftChild == null && curr.rightChild == null){
145 if(curr == root){
146 root = null;
147 return true;
148 }
149 if(isLeft){
150 parent.leftChild = null;
151 }else{
152 parent.rightChild = null;
153 }
154 }else if(curr.leftChild == null){
155 //第二种情况,要删除的结点有一个子节点且是右子结点
156 if(curr == root){
157 root = curr.rightChild;
158 return true;
159 }
160 if(isLeft){
161 parent.leftChild = curr.rightChild;
162 }else{
163 parent.rightChild = curr.rightChild;
164 }
165 }else if(curr.rightChild == null){
166 //第二种情况,要删除的结点有一个子节点且是左子结点
167 if(curr == root){
168 root = curr.leftChild;
169 return true;
170 }
171 if(isLeft){
172 parent.leftChild = curr.leftChild;
173 }else{
174 parent.rightChild = curr.leftChild;
175 }
176 }else{
177 //第三种情况,也是最复杂的一种情况,要删除的结点有两个子节点,需要找寻中序后继结点
178 Node succeeder = getSucceeder(curr);
179 if(curr == root){
180 root = succeeder;
181 return true;
182 }
183 if(isLeft){
184 parent.leftChild = succeeder;
185 }else{
186 parent.rightChild = succeeder;
187 }
188 //当后继结点为删除结点的右子结点
189 succeeder.leftChild = curr.leftChild;
190
191 }
192 return true;
193 }
194 public Node getSucceeder(Node delNode){
195 Node succeeder = delNode;
196 Node parent = delNode;
197 Node currNode = delNode.rightChild;
198 //寻找后继结点
199 while(currNode != null){
200 parent = succeeder;
201 succeeder = currNode;
202 currNode = currNode.leftChild;
203 }
204 //如果后继结点不是要删除结点的右子结点
205 if(succeeder != delNode.rightChild){
206 parent.leftChild = succeeder.rightChild;
207 //将后继结点的左右子结点分别指向要删除结点的左右子节点
208 succeeder.leftChild = delNode.leftChild;
209 succeeder.rightChild = delNode.rightChild;
210 }
211 return succeeder;
212
213 }
214 public static void main(String []args) throws Exception {
215 BinaryTree binaryTree = new BinaryTree();
216 //插入操作
217 binaryTree.insert(5);
218 binaryTree.insert(2);
219 binaryTree.insert(8);
220 binaryTree.insert(1);
221 binaryTree.insert(3);
222 binaryTree.insert(6);
223 binaryTree.insert(10);
224 //前序遍历
225 System.out.println("前序遍历:");
226 binaryTree.preOrder(binaryTree.root);
227 System.out.println();
228 //中序遍历
229 System.out.println("中序遍历:");
230 binaryTree.inOrder(binaryTree.root);
231 System.out.println();
232 //后序遍历
233 System.out.println("后序遍历:");
234 binaryTree.postOrder(binaryTree.root);
235 System.out.println();
236 //查找结点
237 Node node = binaryTree.find(10);
238 System.out.println("找到结点,其值为:"+node.data);
239 //删除结点
240 binaryTree.delete(8);
241 System.out.print("删除结点8,中序遍历:");
242 binaryTree.preOrder(binaryTree.root);
243 }
244 }
执行结果
前序遍历:
5 2 1 3 8 6 10
中序遍历:
1 2 3 5 6 8 10
后序遍历:
1 3 2 6 10 8 5
找到结点,其值为:10
删除结点8,中序遍历:5 2 1 3 10 6
