说起回家,路途漫漫,行李满满,尤其我等村里交通不发达的地方,可能连直达的票都没有,虽说条条大陆通罗马,但毕竟还是想找个换乘最少的路线,毕竟谁不想回家更轻松点呢(*^_^*),下面就是我回家的所有路线。
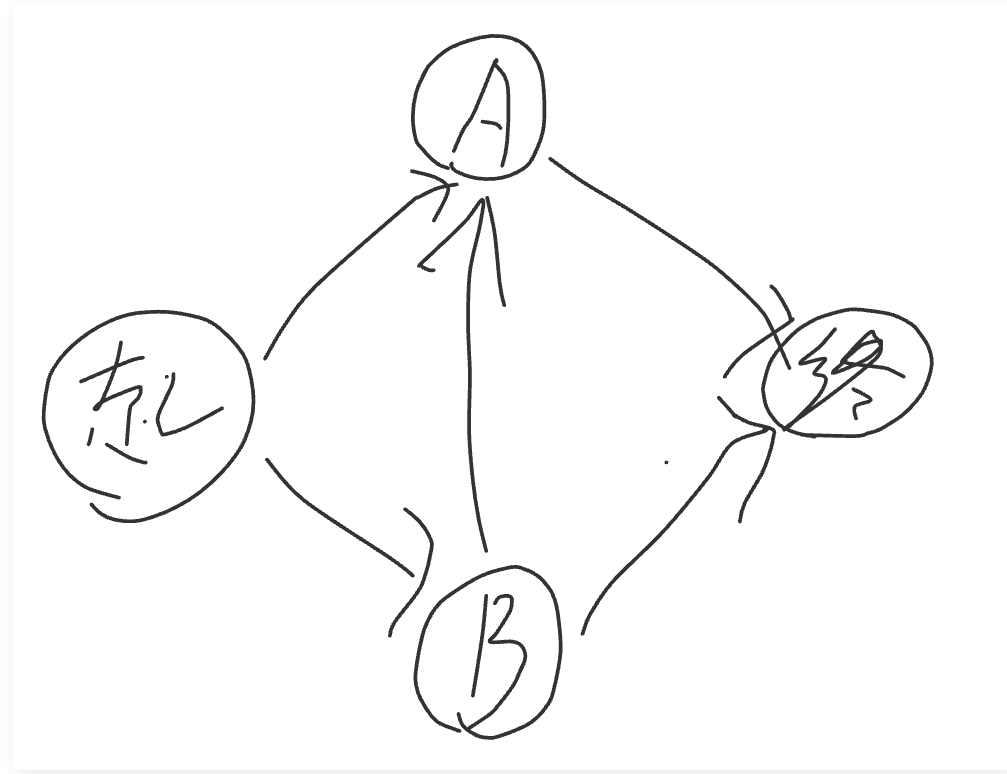
思路很简单,先找起点看是否能到,不能到的话,看起点能到的点的下一步是否能到
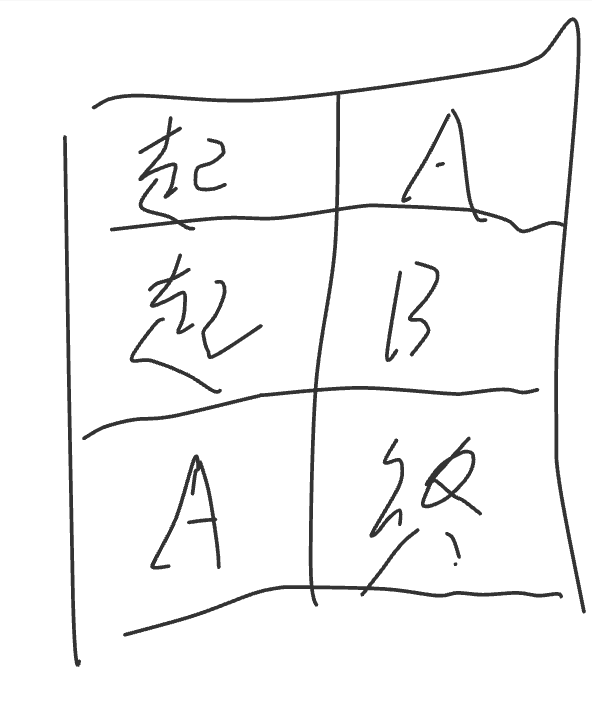
话不多说,撸代码:
public static void main(String[] args) {
HashMap<String,List<String>> data = new HashMap<String, List<String>>();
List<String> list1 = new ArrayList<String>();
data.put("起点",list1);
list1.add("A");
list1.add("B");
List<String> list2 = new ArrayList<String>();
data.put("A",list2);
list2.add("终点");
List<String> list3 = new ArrayList<String>();
data.put("B",list3);
list3.add("A");
list3.add("终点");
query(data,"终点","起点");
}
public static void query(Map<String,List<String>> data, String queryValue, String start){
if(data==null || queryValue ==null){
return;
}
Queue<String> queue = new LinkedList<String>();
Map quaryLog = new HashMap();
Map<String,List<String>> routes = new HashMap<String, List<String>>();
queue.offer(start);
quaryLog.put(start,"");
String parent = null;
while (!queue.isEmpty()){
parent = queue.poll();
List<String> values = data.get(parent);
for(String value:values){
List<String> r = new ArrayList<String>();
if(routes.containsKey(parent)){
r.addAll(routes.get(parent));
}
r.add(parent);
routes.put(value,r);
if(queryValue.equals(value)){
routes.get(value).add(value);
System.out.println(routes.get(value));
return;
}
if(!quaryLog.containsKey(value)){
queue.offer(value);
quaryLog.put(value,"");
}
}
}
return ;
}
run 一把,结果出来了
[起点, A, 终点]
终于,结果出来了,先到A地,再从A到终点,其实这就是广度优先搜索,so easy兴冲冲去买票,发现钱不够,哎,没有考虑票价啊!!!我的票价是这样的:
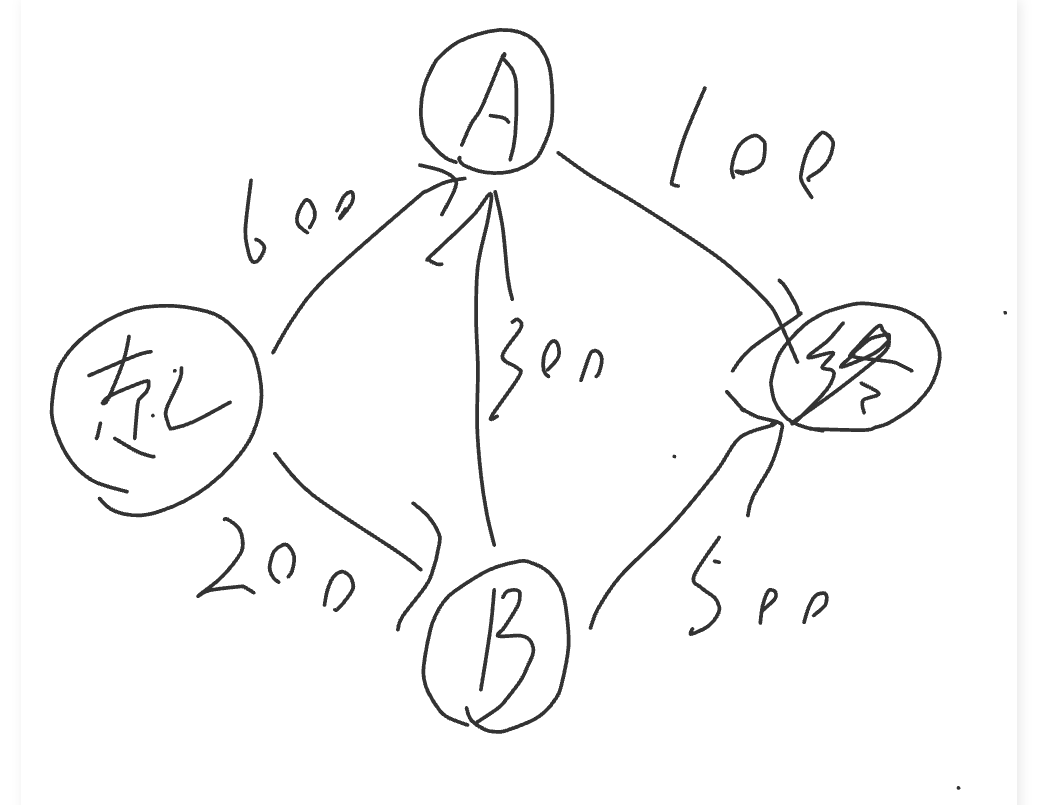
按照现在的规划需要700元,可是我只有650元,不够啊,没办法,修改算法把,这次需要把价钱考虑进去,我需要最便宜的路线
思路也类似,先从起点开始走,分别计算最便宜的路线
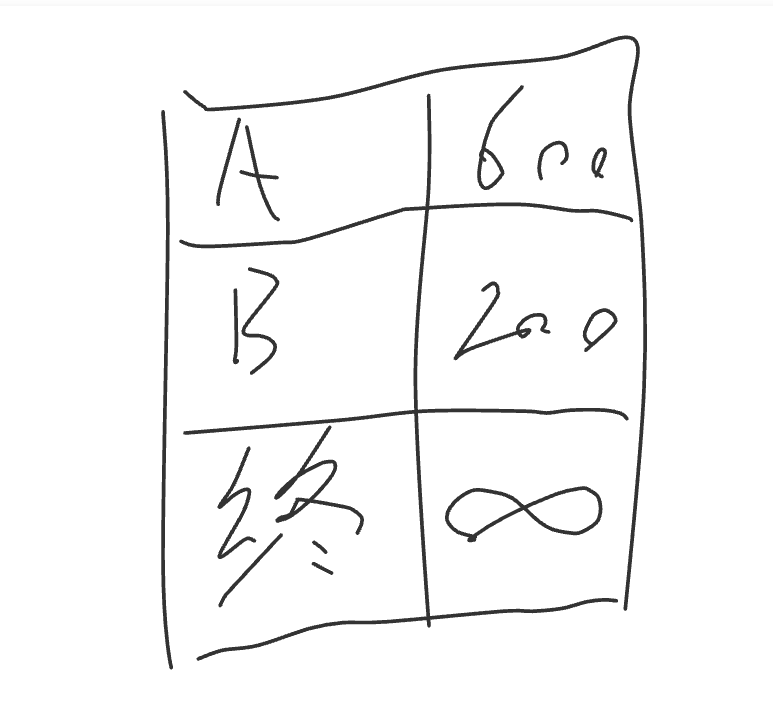
终点暂时到不了,我们把到终点的距离记作无穷,接着我们从B点开始往下找,计算最便宜的价钱如下:

然后再计算A点走的话,最便宜的路线,比从B点走便宜的话我们就更新,不便宜的话代表原来的价钱已经是最便宜的了
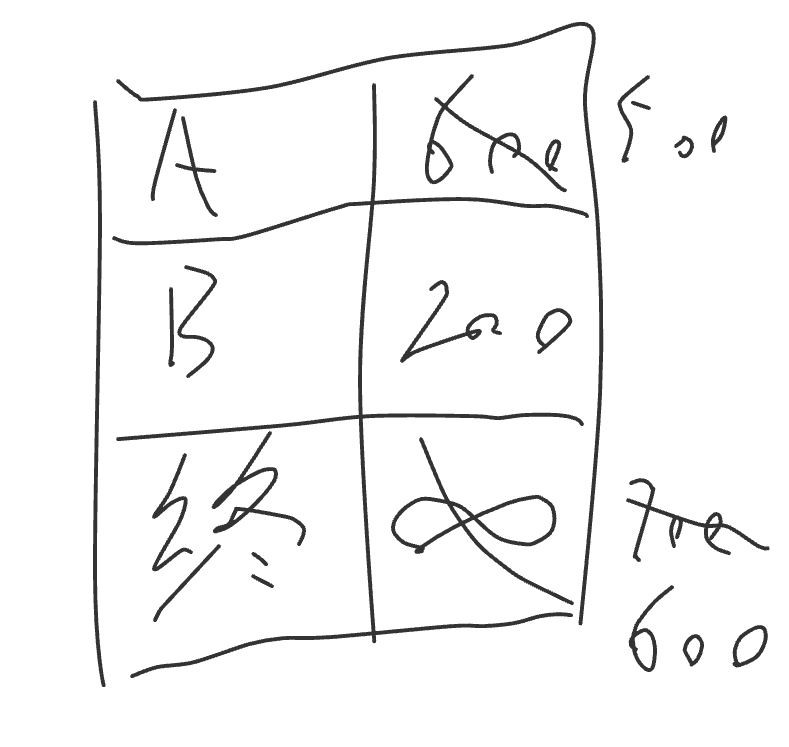
找到了,最便宜的路线是600,但是程序要如何做呢,毕竟我以后不仅要回家,还要去旅游,还要去丈母娘家,我要每次都最便宜!!!,撸码如下:
public static void main(String[] args) {
HashMap<String,HashMap<String,Integer>> data = new HashMap<String, HashMap<String, Integer>>();
HashMap<String,Integer> map1 = new HashMap<String, Integer>();
data.put("起点",map1);
map1.put("A",600);
map1.put("B",200);
HashMap<String,Integer> map2 = new HashMap<String, Integer>();
data.put("A",map2);
map2.put("终点",100);
HashMap<String,Integer> map3 = new HashMap<String, Integer>();
data.put("B",map3);
map3.put("终点",500);
map3.put("A",300);
queryMinPrice(data,"起点","终点");
}
public static void queryMinPrice(HashMap<String,HashMap<String,Integer>> data,String start,String end){
HashMap<String,Integer> costs = new HashMap<String, Integer>();
HashMap<String,List<String>> route = new HashMap<String, List<String>>();
for(Map.Entry<String,Integer> entry: data.get(start).entrySet()){
costs.put(entry.getKey(),entry.getValue());
List<String> list = new ArrayList<String>();
list.add(entry.getKey());
route.put(entry.getKey(),list);
}
costs.put(end,Integer.MAX_VALUE);
HashMap<String,String> queryLog = new HashMap<String, String>();
String key = findMinPriceKey(costs,queryLog);
while (key != null){
queryLog.put(key,"");
if(data.get(key) == null){
break;
}
for(Map.Entry<String,Integer> entry:data.get(key).entrySet()){
if(costs.containsKey(entry.getKey())){
if(entry.getValue()+costs.get(key)<costs.get(entry.getKey())){
costs.put(entry.getKey(),entry.getValue()+costs.get(key));
List<String> list = new ArrayList<String>();
list.addAll(route.get(key));
list.add(entry.getKey());
route.put(entry.getKey(),list);
}
}else {
costs.put(entry.getKey(),entry.getValue()+costs.get(key));
List<String> list = new ArrayList<String>();
list.addAll(route.get(key));
route.put(entry.getKey(),list);
}
}
key = findMinPriceKey(costs,queryLog);
}
System.out.println("最小花费:"+costs.get(end));
System.out.println("最小花费路径:"+route.get(end));
}
private static String findMinPriceKey(HashMap<String,Integer> data,HashMap<String,String> queryLog){
String key = null;
for(Map.Entry<String,Integer> entry : data.entrySet()){
if(!queryLog.containsKey(entry.getKey()) && key == null ){
key = entry.getKey();
}
if(!queryLog.containsKey(entry.getKey()) && entry.getValue()<data.get(key)){
key = entry.getKey();
}
}
return key;
}
运行结果:
最小花费:600
最小花费路径:[B, A, 终点]
结果出来了,先买到B的票,然后在到A,再回家,只要600块,还能省50块,完美!!这就是大名鼎鼎的狄克斯特拉算法。
PS:这不是标准的狄克斯特拉算法,只是本例中的数据少,数据多的话遍历成本是很高的,标准的狄克斯特拉算法利用的是贪婪算法思想,求局部最优解,要在可以到达终点时就返回(此注释基于评论,本来自己写着玩儿的,没想会有人认真来看,避免产生误解,误导他人,水平有限深感惭愧)