Dynamic Network Pruning
2020-AAAI-Dynamic Network Pruning with Interpretable Layerwise Channel Selection
来源:ChenBong 博客园
- Institute:THU, Ant Financal
- Author:Yulong Wu, Xiaolu Zhang, Hang Su*
- GitHub:/
- Citation:/
Introduction
给每个卷积层加上决策单元, 在推理时根据第 i 层的input feature maps, 生成第 i 层的mask, 根据mask来决定第 i 层要激活的卷积核, 并将mask乘在第 i 层的output feature maps 上。
动态剪枝网络可以通过根据不同的输入动态决定推理路径,实现实时线上加速目的。
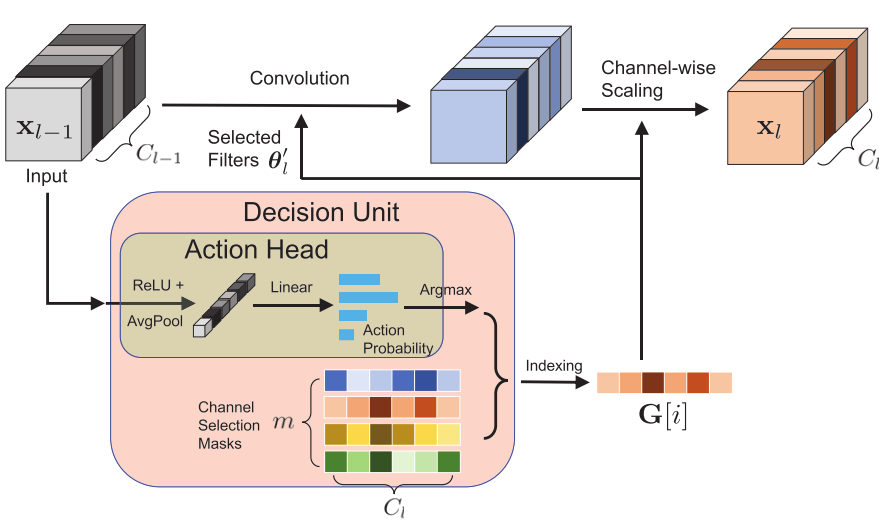
Motivation
之前的方法大多直接对每个权重通道输出连续重要值,来决定权重的使用情况,但缺乏清晰可理解的剪枝过程。
Contribution
Method
Pipleline

图示为第 l 个卷积层, 每个卷积层都会附加一个决策单元(Decision Unit), 每个决策单元又分为2部分:
- Action Head
- 输入 l 层的input feature maps:(x_{l-1})
- (A(x)= Linear(GlobalAvgPool(Relu(x_{l-1})))=[p_1, p_2, ..., p_m], A(x)∈R^m qquad (5))
- (A(x)) 是一个m维向量
- Masks Sets
- 保存第 l 层的 m 种mask:(G_l ∈ R^{m×C_{l}})
- 取 (A(x)) 中最大的 (i=arg max(A(x))) , (G_l[i]) 作为第 l 层运行时的mask
- (G_l[i]∈R^{C{_l}}) ,(G_l[i]) 维度与第 l 层的通道数相同。
- (G_l[i]) 是一个稀疏向量(其中有些元素为0),将 (G_l[i]) 中非0元素对应位置的卷积核进行计算,没有计算的卷积核的output feature map 直接用0填充,得到output feature maps
- 将output feature maps再乘以 (G_l[i]) ,得到第 l 层最终的output feature maps(通道数还是(C_l) )。
Loss
(min _{{Theta, Phi}} mathcal{L}=sum_{h} mathcal{L}_{e n t}left(f_{Theta}left(mathbf{x}_{k} ight), y_{k} ight)+gamma cdot Omegaleft(left{mathbf{G}_{l} ight}_{L} ight) qquad (1))
公式(1)说明:
-
(Theta) :表示网络权重
-
(Phi) :表示所有层的决策单元的参数,包括所有Action Head的权重: ( heta_A) 和 所有层的Masks Sets: ({G_l}_L)
-
(gamma cdot Omegaleft(left{mathbf{G}_{l} ight}_{L} ight)) :表示使得masks稀疏化到指定剪枝率的正则项, (gamma) 为系数(超参)
( (Theta) 使用proximal gradient descent 优化器学习, (Phi) 使用Adam优化器学习)
第 l 层的执行过程

(A(x)= Linear(GlobalAvgPool(Relu(x_{l-1}))), A(x)∈R^m qquad (5))
公式(5)说明:
- 第 l 层的输入x 经过Action Head,输出m为向量
(pi(mathbf{x}, phi)=mathbf{G}[i], where i=arg max A(x) qquad(3))
公式(3)说明:
- 取 (A(x)) 中最大的 (i=arg max(A(x))) ,
(mathbf{x}_{l}=operatorname{conv}left(mathbf{x}_{l-1}, heta_{l} ight) qquad (2))
公式(2)说明:
- 常规卷积
(mathbf{x}_{l}=convleft(mathbf{x}_{l-1}, heta^prime_{l} ight) * pileft(mathbf{x}_{l-1}, phi ight), 其中 heta_{l}^{prime}=left{ heta_{l}[j] mathbf{G}[i][j] eq 0 ight} qquad (4))
公式(4)说明:
- 将 (G_l[i]) 作为第 l 层运行时的mask, (G_l[i]∈R^{C{_l}}) ,(G_l[i]) 维度与第 l 层的通道数相同。
- (G_l[i]) 是一个稀疏向量(其中有些元素为0),将 (G_l[i]) 中非0元素对应位置的卷积核进行计算,没有计算的卷积核的output feature map 直接用0填充,得到output feature maps
- 将output feature maps再乘以 (G_l[i]) ,得到第 l 层最终的output feature maps(通道数还是(C_l) )。
Mask稀疏化正则项
(Omegaleft(left{mathbf{G}_{l} ight}_{L} ight)=left(frac{left|operatorname{concat}left(mathbf{G}_{1}, cdots, mathbf{G}_{L} ight) ight|_{1}}{sum_{l} C_{l}}-r ight)^{2} qquad (8))
公式(8)说明:
- 这里的 ((G_1, G_2, ..., G_L)) 应该是前向过程中,经过 A(x) 选择完的masks,即 (G_1) 是 (C_1) 维的向量,..., (G_L) 是(G_L) 维的向量。
- 所以 (operatorname{concat}left(mathbf{G}_{1}, cdots, mathbf{G}_{L} ight)) 是 (sum_{l} C_{l}) 维的向量
- (frac{left|operatorname{concat}left(mathbf{G}_{1}, cdots, mathbf{G}_{L} ight) ight|_{1}}{sum_{l} C_{l}}) 表示每个卷积核的 mask 的平均稀疏程度,而L1-norm会使G稀疏化(有的项变为0),作为网络的总稀疏程度
- r 为指定的剪枝率
(arg max A(x))松弛,可微分处理

(A(x)= Linear(GlobalAvgPool(Relu(x_{l-1})))=[p_1, p_2, ..., p_m], A(x)∈R^m qquad (5))
(pi(mathbf{x}, phi)=mathbf{G}[i], where i=arg max A(x) qquad(3))
图中的 (arg max) 步骤是不可微分的,因此作以下松弛处理(和DARTS几乎相同的处理方法):
(I_{i}=frac{exp left(left(log p_{i}+G_{i} ight) / au ight)}{sum_{j=1}^{m} exp left(left(log p_{j}+G_{j} ight) / au ight)}, quad forall i=1, cdots, m qquad (7))
公式(7)说明:
- 其中 (p_i) 为原始输出概率, (G_i) 为 Gumbel 随机变量(添加微小的扰动,增加随机性), (τ) 为温度系数(超参)。
- 将 ([p_1, p_2, ..., p_m]) 转化为 ([I_1, I_2, ..., I_m])
- 最终 (x_l = sum_{i=1}^m I_i cdot G[i] cdot x_l)
- 使得arg max 操作转变为矩阵乘法操作
Experiments
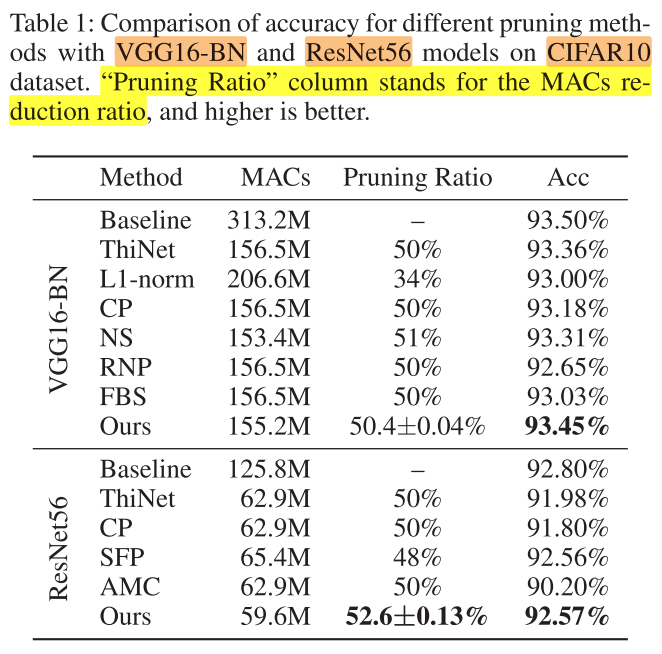
CIFAR-10
Settings
- 每层的决策单元,masks组数m=5
- 稀疏率r = 0.1 for VGG16-BN, r=0.4 for ResNet-56
- batch size=128
- train epoch=100
- train learning rate = 0.01
- fine-tune learning rate = 0.001
Result
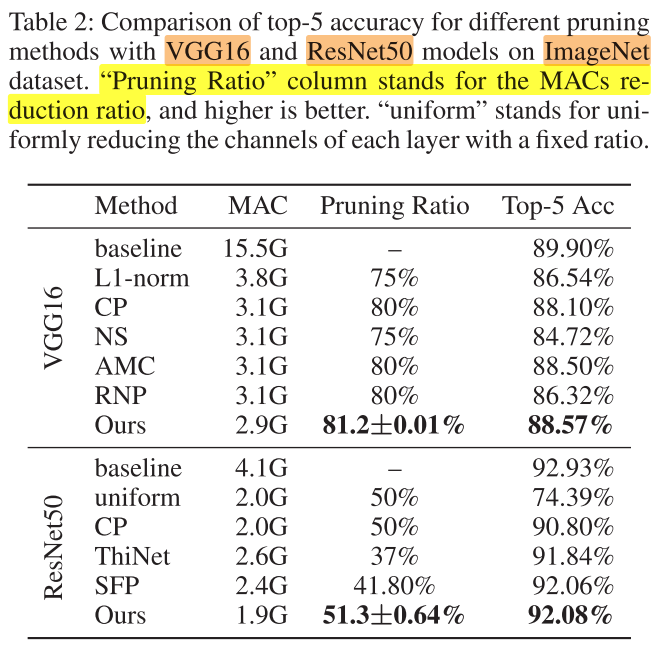
ImageNet
Settings
- 每层的决策单元,masks组数m=40
- 稀疏率r = 0.6 for VGG16 and ResNet-50
- batch size=64
- 基于pretrain compressed model
- train epoch=30
- train learning rate = 0.01
- fine-tune learning rate = 0.001
Result
Action Numer m
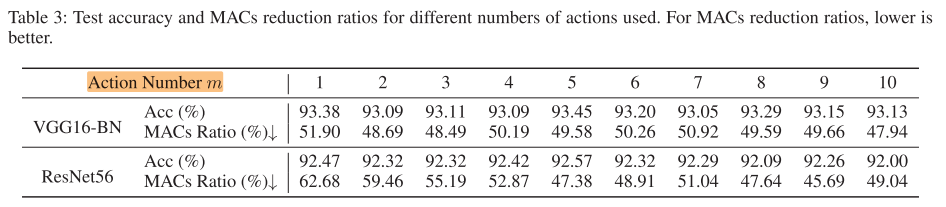
表3说明:
- 对于VGG16-BN,m的影响不大
- 对于ResNet-56,m=5左右acc较高,m太小和太大都会导致acc降低
决策路径可视化
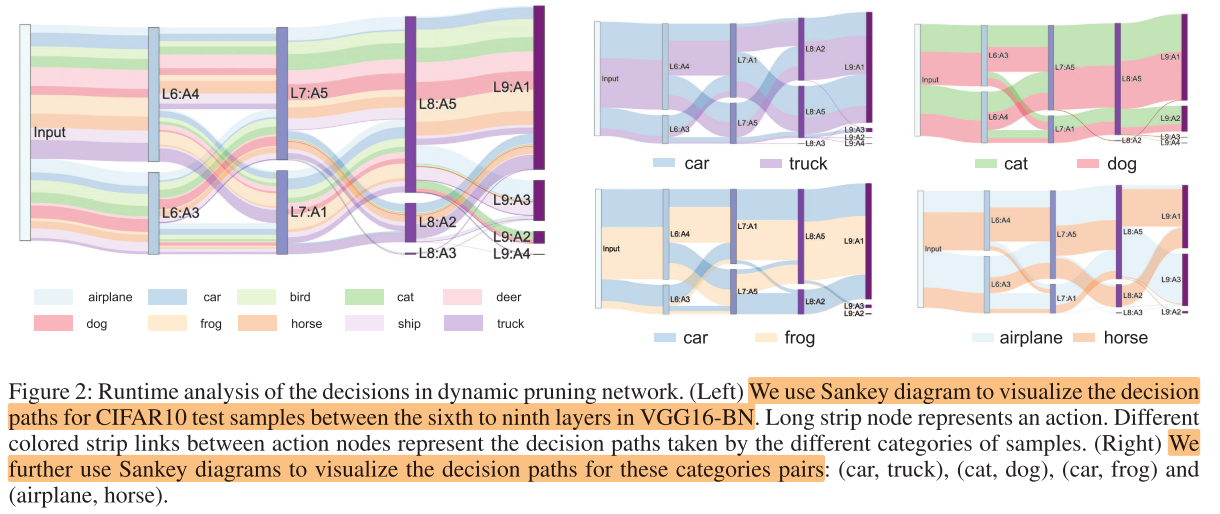
与其他动态剪枝方法(FBS)分类对比
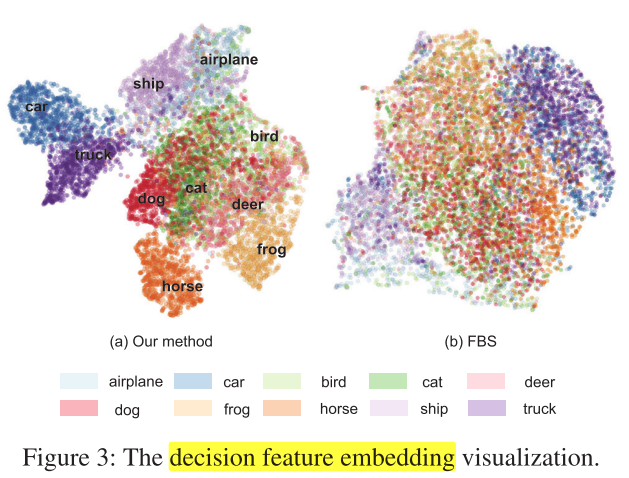
图3说明:
- 每个样本经过每个决策单元,会得到一个离散的概率向量 (left{mathbf{p}_{l} in mathcal{R}^{m} mid l=1, cdots, L ight}) ,可以作为该样本的feature embedding,用来分类
对抗样本实验

图4说明:
- 左中右分别为3种不同的对抗攻击算法(用不同算法生成对抗样本)
- 彩色点为原始样本,灰色点为对抗样本
- 可以看出,在本文的原始样本与对抗样本的区别还是比较大的
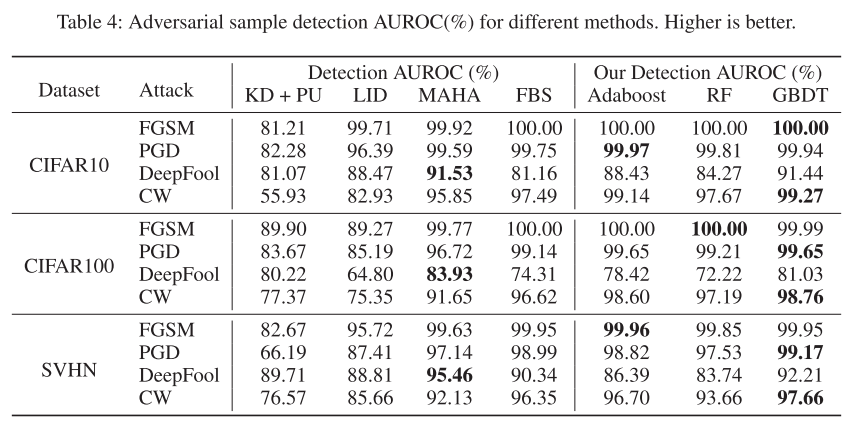
Conclusion
Summary
- 由动态剪枝到使用动态剪枝的路径概率向量来编码样本,作为对抗样本的检测,很新颖,以前没见过