K-Means 鸢尾花分类

目录

• 前言
• K-Means
  • 原理
  • 步骤
  • 相似度
  • 缺点
• 代码实例
• 运行截图

前言

机器学习按照有无标签可以分为“监督学习”和“非监督学习”

1. 监督学习代表算法：SVM、逻辑回归、决策树、各种集成算法等等。

   非监督学习代表算法：K-Means算法（聚类算法中最著名的算法）、两步聚类、Kohonen等。

2. 学习方式不同。聚类是一种非监督式学习算法，而分类是监督式学习算法

3. 对源数据集要求不同。聚类不要求源数据集有标签，但分类需要标签用来做学习

4. 应用场景不同。聚类一般应用于做数据探索性分析，而分类更多的用于预测性分析

5. 解读结果不同。聚类算法的结果是将不同的数据集按照各自的典型特征分成不同类别，不同人对聚类的结果解读可能不同；而分类的结果却是一个固定值，不存在不同解读的情况

聚类分析的基本思想是“物以类聚、人以群分”，因此大量的数据集中必然存在相似的数据点，基于这个假设就可以将数据区分出来，并发现每个数据集（分类）的特征

K-Means

原理

K-Means是典型的聚类算法，K-Means算法中的k表示的是聚类为k个簇，means代表取每一个聚类中数据值的均值作为该簇的中心，或者称为质心，即用每一个的类的质心对该簇进行描述。

步骤

1. 创建k个点作为起始质心。
2. 计算每一个数据点到k个质心的距离。把这个点归到距离最近的哪个质心。
3. 根据每个质心所聚集的点，重新更新质心的位置。
4. 重复2，3，直到前后两次质心的位置的变化小于一个阈值。

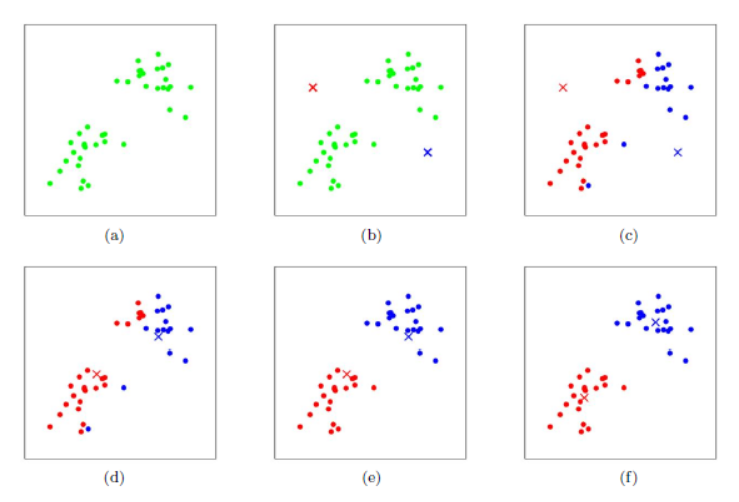
具体变化过程（k=2的K-Means）：

相似度

聚类首先面临的一个问题是，如何衡量不同数据之间的“相似度”。大多数“相似度”都是基于距离计算的，距离计算可以分为两类。

1. 基于几何距离的“相似度”：欧式距离、曼哈顿距离、切比雪夫距离
2. 基于非几何距离的“相似度”：余弦距离、汉明距离、相关系数

一般会选择欧氏距离计算相似度，但我们会发现不同维度间由于度量单位的差异，计算的结果值会产生很大差异。例如假设A和B两个点分别具有两个维度：订单金额和转化率，那么订单金额的取值范围可能是0到无穷大，而转化率的取值为0到1，因此计算结果会由于订单金额的取值范围而“片面”夸大了这一维度的计算比重。所以大多数情况下，如果存在这种度量量级的差异会选择数据标准化，使不同维度落到相同的数据区间内然后进行计算。注：上面说到大多数情况下需要标准化，就意味着不是所有的场景下都需要标准化，一种是原有的数据维度之间的量级差异不大，因此没有必要标准化；二是标准化后的结果在解读时会出现难以还原的问题，例如原本均值为180在标准化后可能就是0.31，而这个数据很难还原，只能进行相对其他维度的解读

缺点

• 既然基于均值计算，那么要求簇的平均值可以被定义和使用，此时字符串等非数值型数据则不适用。

• K-Means的第一步是确定k（要生成的簇的数目），对于不同的初始值K，可能会导致不同结果。

• 应用数据集存在局限性，适用于球状或集中分布数据，不适用于特殊情况数据。如下面这种非球状的数据分布就无法正确分类。

  

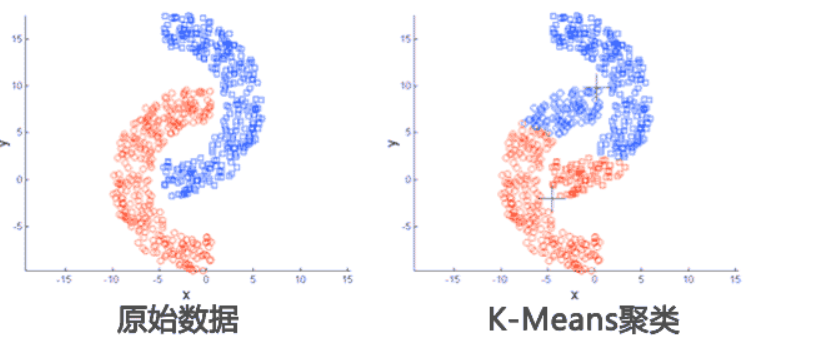
• 它对于“躁声”和孤立点数据是敏感的，少量的该类数据能够对平均值产生极大的影响。

代码实例

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D #3D的库

from sklearn.cluster import KMeans
from sklearn import datasets

np.random.seed(5) #设置随机数种子
#加载数据集
iris = datasets.load_iris()
#data里面是花萼长度、花萼宽度、花瓣长度、花瓣宽度的测量数据，格式为numpy数组，总共150条数据，分为三类每类50个
X = iris.data
#记录花的的类别用0、1、2标识
y = iris.target

#n_clusters : 聚类的个数k
estimators = [('k_means_iris_8', KMeans(n_clusters=8)),#k=8的kmeans
              ('k_means_iris_3', KMeans(n_clusters=3)), #k=3的kmeans
              ('k_means_iris_bad_init', KMeans(n_clusters=3, n_init=1,init='random')) #k=3，随机初始化的kmeans
              ]
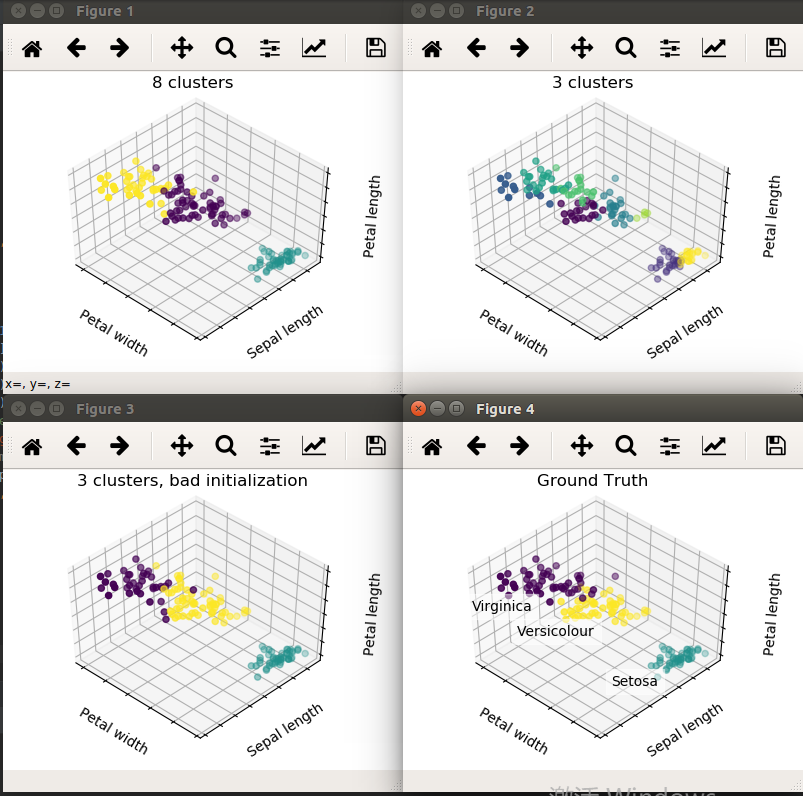
#对数据用k=8去聚类。因为数据本身只有3类，所以聚类效果不好。
#对数据用k=3去聚类，效果不错。
#还是用k=3去聚类，但是改变初始化方式init=random，n_init=1，这样的随机初始化，最后的效果会不好。
#最后一张图是数据本身的label，和第二幅相差不大。
fignum = 1
titles = ['8 clusters', '3 clusters', '3 clusters, bad initialization']
for name, est in estimators:
    #创建自定义图像
    fig = plt.figure(fignum, figsize=(4, 3))
    #画三维图
    ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
    est.fit(X) #fit建立模型
    labels = est.labels_ #获得模型聚类后的label

    ax.scatter(X[:, 3], X[:, 0], X[:, 2],
               c=labels.astype(np.float), edgecolor='k') #绘制X中的第3，0，2个维度的特征，也就是用花萼长度、花瓣长度、花瓣宽度三个特征绘图

    ax.w_xaxis.set_ticklabels([])
    ax.w_yaxis.set_ticklabels([])
    ax.w_zaxis.set_ticklabels([])
    ax.set_xlabel('Petal width') #设置坐标轴名
    ax.set_ylabel('Sepal length')
    ax.set_zlabel('Petal length')
    ax.set_title(titles[fignum - 1]) #设置图的名字
    ax.dist = 12
    fignum = fignum + 1

# 绘制数据真实标签
fig = plt.figure(fignum, figsize=(4, 3))
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)

for name, label in [('Setosa', 0),
                    ('Versicolour', 1),
                    ('Virginica', 2)]:
    ax.text3D(X[y == label, 3].mean(), #寻找特征的均值点
              X[y == label, 0].mean(),
              X[y == label, 2].mean() + 2, name,
              horizontalalignment='center',
              bbox=dict(alpha=.2, edgecolor='w', facecolor='w'))

y = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=y, edgecolor='k')

ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
ax.set_title('Ground Truth')
ax.dist = 12

fig.show() #绘制整张图

运行截图

参考博客：http://www.dataivy.cn/blog/k均值k-means/