我通过三个实例代码的学习了解到了线性回归的大致概念
一、实例一
import numpy as np import tensorflow.compat.v1 as tf import matplotlib.pyplot as plt tf.disable_v2_behavior() # 随机生成1000个点,围绕在y=0.1x+0.3的直线周围 num_points = 1000 vectors_set = [] for i in range(num_points): x1 = np.random.normal(0.0, 0.55) y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03) vectors_set.append([x1, y1]) # 生成一些样本 x_data = [v[0] for v in vectors_set] y_data = [v[1] for v in vectors_set] plt.scatter(x_data,y_data,c='r') plt.show()
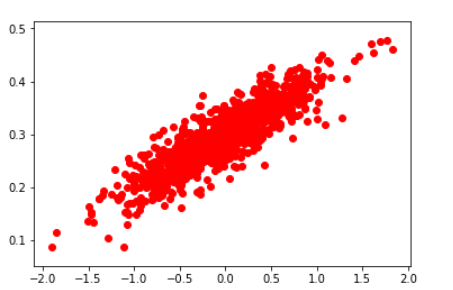
# 生成1维的W矩阵,取值是[-1,1]之间的随机数类似于[1,0.5,-0.5,0.6,0.7,0.8,0.2,0.4] W = tf.Variable(tf.random_uniform([1], -1.0, 1.0), name='W') # 生成1维的b矩阵,初始值是0 b = tf.Variable(tf.zeros([1]), name='b') # 经过计算得出预估值y(矩阵运算) y = W * x_data + b # 以预估值y和实际值y_data之间的均方误差作为损失 loss = tf.reduce_mean(tf.square(y - y_data), name='loss') # 采用梯度下降法来优化参数 optimizer = tf.train.GradientDescentOptimizer(0.5) # 训练的过程就是最小化这个误差值 train = optimizer.minimize(loss, name='train') sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) # 初始化的W和b是多少 print ("W =", sess.run(W), "b=", sess.run(b), "loss =", sess.run(loss)) # 执行20次训练 for step in range(30): sess.run(train) # 输出训练好的W和b print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss)) writer = tf.summary.FileWriter("./tmp", sess.graph)

plt.scatter(x_data,y_data,c='r') plt.plot(x_data,sess.run(W)*x_data+sess.run(b)) plt.show()
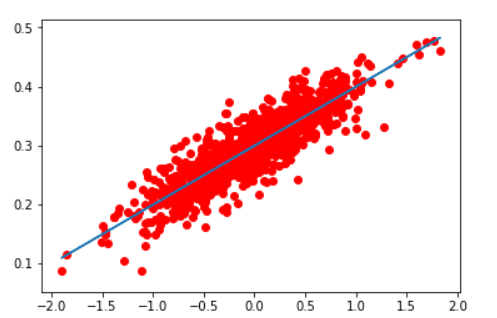
我这段实例代码的大致理解是:
1、创建训练数据集:随机生成一些围绕在y=0.1x+0.3
2、设置模型的初始权重:因为我们知道模型是线性的也就是y=wx+b,所以去初始化w、b
3、构造线性回归模型(这个代码中也就是计算预估值y):因为我们知道模型是线性的也就是y=wx+b,前面也初始化w、b了,那就能根据输入的x_data得到该模型求出预估值y
4、求损失函数,即均方差
5、使用梯度下降法得到损失的最小值,即最优解
6、开始训练模型、得出模型的代价函数、可视化
二、实例二
import tensorflow.compat.v1 as tf import numpy as np import matplotlib.pyplot as plt import os tf.disable_v2_behavior() os.environ["CUDA_VISIBLE_DEVICES"]="0" learning_rate=0.01 training_epochs=1000 display_step=50 #生成样本 train_X=np.asarray([3.3,4.4,5.5,6.71,6.93,4.168,9.779,6.182,7.59,2.167,7.042,10.791,5.313,7.997,5.654,9.27,3.1]) train_Y=np.asarray([1.7,2.76,2.09,3.19,1.694,1.573,3.366,2.596,2.53,1.221,2.827,3.465,1.65,2.904,2.42,2.94,1.3]) n_samples=train_X.shape[0] X=tf.placeholder("float") Y=tf.placeholder("float") # 生成1维的W矩阵,取值是[-1,1]之间的随机数类似于[1,4,5,6,7,8,2,4] W=tf.Variable(np.random.randn(),name="weight") b=tf.Variable(np.random.randn(),name='bias') #tf.multiply将两个矩阵中对应元素各自相乘,tf.add将两个矩阵中对应元素各自相加 pred=tf.add(tf.multiply(X,W),b) #求损失函数 cost=tf.reduce_sum(tf.pow(pred-Y,2))/(2*n_samples) #梯度下降优化 optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) init =tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) for epoch in range(training_epochs): for (x,y) in zip(train_X,train_Y): sess.run(optimizer,feed_dict={X:x,Y:y}) if (epoch+1) % display_step==0: c=sess.run(cost,feed_dict={X:train_X,Y:train_Y}) print("Epoch:" ,'%04d' %(epoch+1),"cost=","{:.9f}".format(c),"W=",sess.run(W),"b=",sess.run(b)) print("Optimization Finished!") plt.plot(train_X,train_Y,'ro',label='Original data') plt.plot(train_X,sess.run(W)*train_X+sess.run(b),label="Fitting line") plt.legend() plt.show()
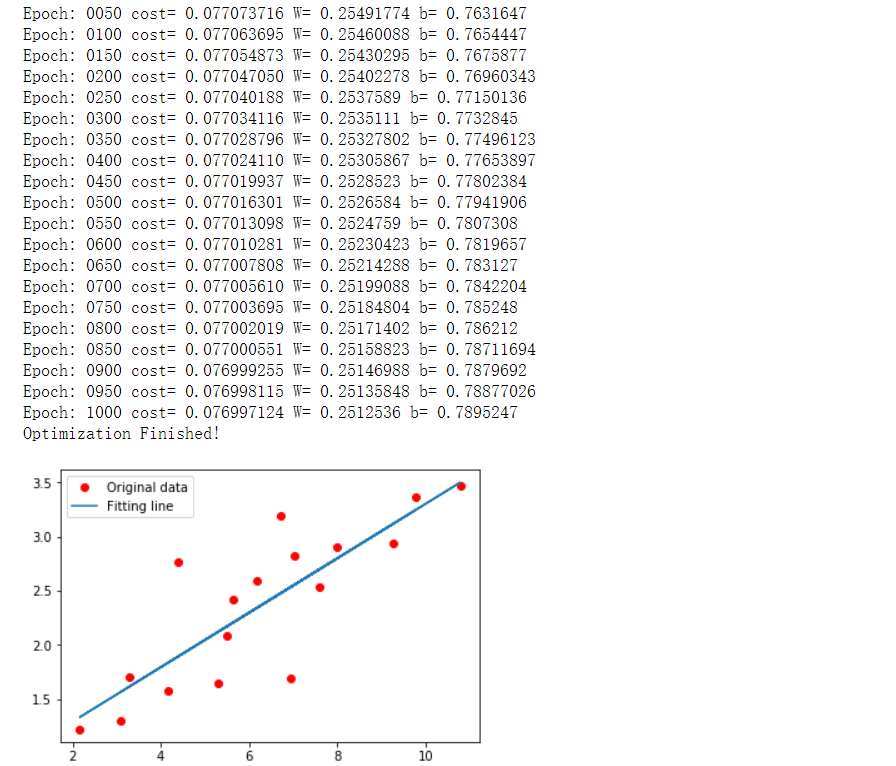
实例二和实例一的大致思路是一样的,只是创建训练数据集、建立模型、开始训练模型的方法不一样
三、实例三
import numpy as np import pandas as pd import tensorflow.compat.v1 as tf import matplotlib.pyplot as plt tf.disable_v2_behavior() # 随机生成1000个点,围绕在y=0.1x+0.3的直线周围 num_points = 1000 vectors_set = [] for i in range(num_points): x1 = np.random.normal(0.0, 0.55) y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03) vectors_set.append([x1, y1]) # 生成一些样本 x_data = [v[0] for v in vectors_set] y_data = [v[1] for v in vectors_set] plt.scatter(x_data,y_data,c='r') plt.show()
model = tf.keras.Sequential() model.add(tf.keras.layers.Dense(1, input_shape=(1,))) model.summary()

model.compile(optimizer='adam', loss='mse' )
history=model.fit(x_data,y_data,epochs=500)
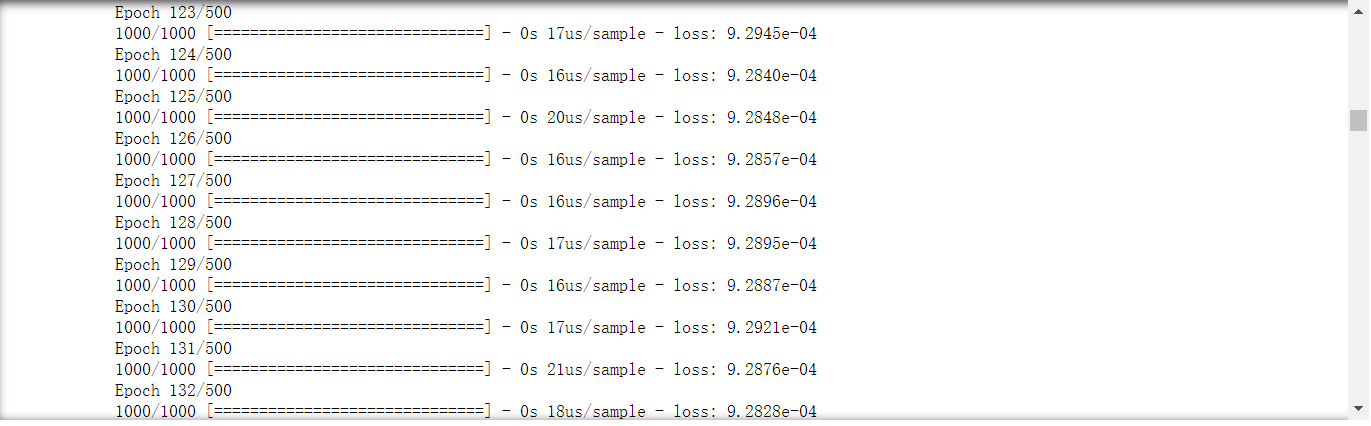
model.predict(pd.Series([20,10,50]))
