牛顿法(Newton Method)
0.引言
与梯度下降法一样,牛顿法也是求解无约束优化问题最早使用的经典算法之一,其基本思想是用迭代点出的一阶导数(梯度)和二阶导数(Hessian矩阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似较小点。
Hessian矩阵是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。可用于判定函数的极值。函数 f(${x_1}$, ${x_2}$, ${x_3}$, ..., ${x_n}$)的Hessian矩阵如下:
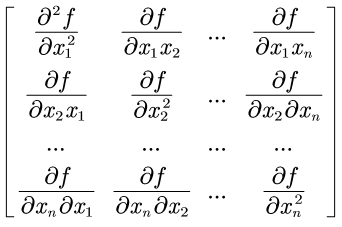
函数的Hessian矩阵具有如下性质:
![]()
![]()
![]()
1.定理
设函数f(x)有二阶连续偏导数,在局部极小点x*处,G(x*)(Hessian矩阵)是正定的并且G(x)在x*的一个邻域内是Lipschitz连续的。如果初始点x0充分靠近x*,那么对一切k,牛顿迭代公式(1)是实定的,当${x_k}$为无穷点列时,其极限为x*且收敛阶至少是二阶的。[1]
2.基本迭代公式:

可推出牛顿迭代法基本公式:[{x_{k + 1}} = {x_k} + G_k^{ - 1}{g_k}qquad(式1)[1]]
3.改进
牛顿法的优点是具有二阶收敛速度,但当Hessian矩阵不正定时,不能保证所产生的方向是目标函数在该点处的下降方向。特定地,当Hessian矩阵奇异时,算法就无法继续进行下去。尽管修正牛顿法可以克服这一缺陷,但其中修正参数$u_k$的选取很难把握,过大或过小都会影响到收敛速度。此外,牛顿法的每一次迭代步都需要目标函数的二阶导数,对于大规模问题其计算量是惊人的。拟牛顿法可以克服这些缺点,并且在一定条件下,这类算法仍然具有较快的收敛速度-超线性收敛速度。[1]
4.一些问题
(1)深度学习为什么不采用牛顿法及其变体?[5]
- 牛顿法涉及到一阶导数(计算梯度)和二阶导数(就算Hessian矩阵),计算量大。
- 对于凸函数,牛顿法迭代方向一定是目标函数下降方向;然而对于深度学习,目标函数一般非凸函数,故使用牛顿法无法保证一定会使目标函数下降。
参考文献
[1]马昌凤.最优化方法及其Matlab程序设计.北京:科学出版社,2010:33,51
[2]https://blog.csdn.net/yzxnuaa/article/details/79725736
[3]https://www.cnblogs.com/baowee/p/9575408.html
[4]https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/87220341
[5]https://blog.csdn.net/PKU_Jade/article/details/80993057