RE.从单链表开始的数据结构生活（bushi

单链表

单链表中节点的定义

typedef struct LNode{
  int data;//数据域
  struct LNode *next;//定义一个同类型的指针，指向该节点的后继节点
}LNode, *Linklist;

LNode是一个数据节点，而单链表是用指针将许多数据节点连接起来的一个线性表

最开始看单链表代码的时候，我就一直有一个非常非常大的疑问，这个疑问就是：LNode和LinkList到底有什么区别，什么时候要加 * ，什么时候不加 *等等问题， 但这些问题几乎没人人解答，就一直卡着我，导致我特别抵触单链表，看见漫天的指针就烦，也就一直没提起兴趣写链表，但现在可能是代码看多了，发现这玩意也没有那么难搞

我们定义单链表的时候，可以有两种定义方法：LNode *L，或者是LinkList L；通常来说是用的第二种，为什么呢？首先，我要说的是，我们定义的链表为L，这个L其实是一个LNode类型的指针，是整个链表的头节点，我们一旦有了这个头节点，就可以对这个链表进行一系列操作

而这个链表的头节点，他是一个节点而不是一个表；所以就有了第一个定义方法，LNode *L，但这样总的看起来就没有个像表的样子，给人一种很low的感觉，所以所以我们就定一个LNode形的指针为LinkList，这样以后一旦我们需要定义一个单链表，也就是只需要直接 LinkList L一下即可，现在你看这个LinkList是不是有内味了(>_<)

而为什么要在LinkList前面加个 * 呢，我认为是这样滴：把这个LinkList定义为一个节点类型的指针，是为了之后对函数穿参数时，进行链表的修改，因为你如果是在主函数里面创建的链表，你想要利用函数改变其数据，就必须传链表的地址进去，不然是改变不了链表的数据滴

初始化带头节点的链表

void InitLinkList(LinkList &L){
  L = (LinkList)malloc(sizeof(LNode));//这个头节点本质上还是个节点，所以创建空间的时候还是要创建LNode大小的空间
  L->next = NULL;//别忘了让头指针next指向NULL，不然就成了野指针
}

头插法创建单链表

void HeadInsert_LinkList(LinkList &L, int n){//头插法
    LNode *s;//辅助指针，用来申请新的空间，并将输入的数据存进链表
    for(int i = 1; i <= n; ++i){
        s = (LNode*)malloc(sizeof(LNode));//申请一个LNode节点的空间
        cin>>s->data;//输入数据域
        s->next = L->next;//将头结点的next指针指向的点赋给s的next指针，就类似于你要插队，就先要先把脚插进去，人才能进去
        L->next = s;//再把s指针便成头节点后的第一个数据，也就是相当于把人的身体塞进去辽
    }
}

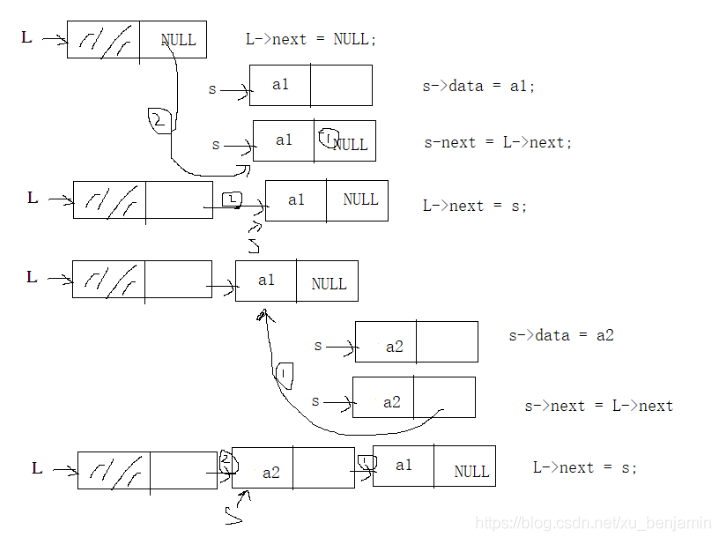
利用头插法建立单链表，输入的数据的顺序与生成的链表中的元素的顺序相反。每个节点插入的时间复杂度为O(1)，总时间复杂度为O(n)。

尾插法建立单链表

void RailInsert_LinkList(LinkList &L, int n){//尾插法
    LNode *s, *r;//s还是和头插一样，r用于始终指向尾节点，这样可以避免每一次尾插都得循环跑到最后一个位置再插
    r = L;//因为是从无到有，所以先让尾指针指向头指针
    for(int i = 1; i <= n; ++i){
        s = (LNode*)malloc(sizeof(LNode));//开辟空间
        cin>>s->data;//输入数据域
        r->next = s;//r代表的是目前的尾节点，s是新来的节点，尾插自然让之前的尾节点（r）的next指向新的尾节点（s）
        r = s;//尾节点改变了，自然要让s变成尾节点
    }
    r->next = NULL;//注意要给尾节点的next赋NULL，不然你要是以后循环就找不到循环结束条件了
}

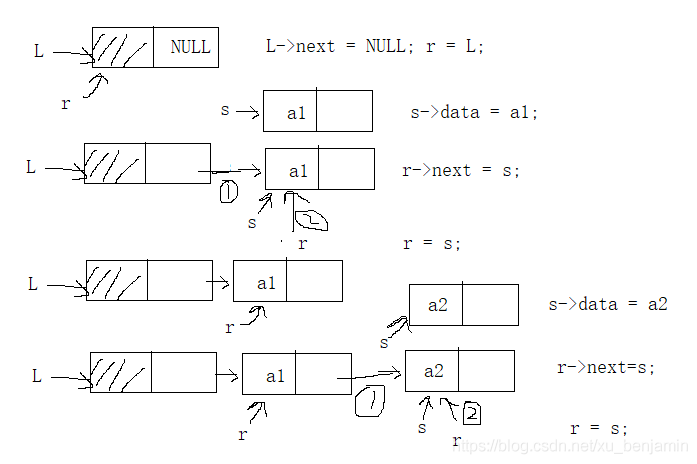
尾插法建立单链表，输入的数据的顺序与生成的链表中的元素的顺序相同。每个结点插入的时间复杂度为O(1)，总时间复杂度为O(n)。

在单链表中插入一个结点

void Insert_LinkList(LinkList &L, int location, int elem){
    LNode *p, *s;//p用于遍历单链表，s用于存储插入的数据elem
    p = L;//p初始指向头节点
    int j = 1;//计数，用来找到需要插入的位置location,且这里一定要是1，不然就会变成插在pos后面了
    while (p != NULL && j < location) {//p不能出链表外，且j小于location的值
        p = p->next;
        ++j;
    }
    s = (LNode*)malloc(sizeof(LNode));//申请空间
    s->data = elem;//赋值
    s->next = p->next;//因为p的位置其实是location-1，p的下一个才是需要插入的地方，所以我们就把p->next的值赋值给s的next，和上面说的一样，先把脚伸进去
    p->next = s;//再把身体塞进去，也就是让前一个节点（p）指向新插入的节点（s）
}

在单链表中删除一个节点

void Delet_LinkList(LinkList &L, int pos){
    LNode *s, *p;//p指向pos前一个位置， s指向pos的位置
    p = L;//将p赋值为L
    int j = 1;//计数，一定是赋值为1
    while (p!=NULL && j < pos) {
        ++j;
        p = p->next;
    }
    s = p->next;//s指向的是pos
    p->next = s->next;//s->next指向的是pos后面的位置，将pos后面的点接到pos前面的节点去，就相当于删掉了pos这个节点
}

按顺序打印单链表

void Print_LinkList(LinkList L){
    LNode* p = L->next;//用于遍历链表，注意是指向L->next
    while (p != NULL) {
        cout<<p->data<<' ';
        p = p->next;
    }
    cout<<endl;
}

测试代码

#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using  namespace std;
#define inf 0x3f3f3f3f
#define MAX 10000 + 50
#define endl '
'
//#define mod 1000000007
//const int mod = 1e9 + 7;
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
//不开longlong见祖宗！
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

typedef struct LNode{
    int data;
    struct LNode *next;
}LNode, *LinkList;

void InitLinkList(LinkList &L){//生成带头结点的单链表L
    L = (LinkList)malloc(sizeof(LNode));
    L->next = NULL;//千万别忘了让头节点的next指向空
}

void HeadInsert_LinkList(LinkList &L, int n){//头插法
    LNode *s;//辅助指针，用来申请新的空间，并将输入的数据存进链表
    for(int i = 1; i <= n; ++i){
        s = (LNode*)malloc(sizeof(LNode));//申请一个LNode节点的空间
        cin>>s->data;//输入数据域
        s->next = L->next;//将头结点的next指针指向的点赋给s的next指针，就类似于你涉足两个人之间，要先把脚插进去，人才能进去
        L->next = s;//再把s指针便成头节点后的第一个数据，也就是相当于把人的身体塞进去辽
    }
}

void RailInsert_LinkList(LinkList &L, int n){//尾插法
    LNode *s, *r;//s还是和头插一样，r用于始终指向尾节点，这样可以避免每一次尾插都得循环跑到最后一个位置再插
    r = L;//因为是从无到有，所以先让尾指针指向头指针
    for(int i = 1; i <= n; ++i){
        s = (LNode*)malloc(sizeof(LNode));//开辟空间
        cin>>s->data;//输入数据域
        r->next = s;//r代表的是目前的尾节点，s是新来的节点，尾插自然让之前的尾节点（r）的next指向新的尾节点（s）
        r = s;//尾节点改变了，自然要让s变成尾节点
    }
    r->next = NULL;//注意要给尾节点的next赋NULL，不然你要是以后循环就找不到循环结束条件了
}

void Insert_LinkList(LinkList &L, int location, int elem){
    LNode *p, *s;//p用于遍历单链表，s用于存储插入的数据elem
    p = L;//p初始指向头节点
    int j = 1;//计数，用来找到需要插入的位置location,且这里一定要是1，不然就会变成插在pos后面了
    while (p != NULL && j < location) {//p不能出链表外，且j小于location的值
        p = p->next;
        ++j;
    }
    s = (LNode*)malloc(sizeof(LNode));//申请空间
    s->data = elem;//赋值
    s->next = p->next;//因为p的位置其实是location-1，p的下一个才是需要插入的地方，所以我们就把p->next的值赋值给s的next，和上面说的一样，先把脚伸进去
    p->next = s;//再把身体塞进去，也就是让前一个节点（p）指向新插入的节点（s）
}

void Print_LinkList(LinkList L){
    LNode* p = L->next;//用于遍历链表，注意是指向L->next
    while (p != NULL) {
        cout<<p->data<<' ';
        p = p->next;
    }
    cout<<endl;
}

int main(){
    LinkList L;//创建以L为头节点的链表
    InitLinkList(L);

    int n;
    cin>>n;
    HeadInsert_LinkList(L, n);//头插法建立n个数的链表
    Print_LinkList(L);

    InitLinkList(L);
    RailInsert_LinkList(L, n);//尾插法建立n个数的链表
    Print_LinkList(L);

    int pos, elem;
    cin>>pos>>elem;
    Insert_LinkList(L, pos, elem);//在pos的位置插入elem
    Print_LinkList(L);
  
    return 0;
}

双向链表

简单介绍：

我们把用链表比作下棋，单链表就是老实人，只能一步步的下，发现哪一步下错了，是没法悔棋的，只能从头再来

而双向链表就像是个开脚本的小猴子，发现自己前面有哪一步下错了，就可以无限悔棋去更正……

双向链表的定义：

typedef struct LNode{
    int val;//值
    struct LNode *next, *pre;//每个节点都有next指针和pre指针，next指针指向下一个节点，pre指针指向上一个节点
}LNode, *De_LinkList;

初始化

void Init_De_LinkList(De_LinkList &L){//
    L = (De_LinkList)malloc(sizeof(LNode));
    L->next = NULL;
    L->pre = NULL;
}
//初始化其实初始化的是头节点，是可以放在创建函数里面的，不过我喜欢将其重新定义为一个函数（好歹也是链表的大哥大，不得给它个面子嘛

头插法创建双向链表

头插法的关键是头不存储信息，让每一个新来的节点都插到头的后面去

看图我们可以知道，对于新来的节点cnt，需要先让cnt的next指针指向nex去（相当于上面单链表中说的先把脚伸进去），再让nex的pre指针指向cnt，再让cnt的pre指针指向头节点pr，最后再让pr的next指针指向cnt即可

需要注意的是，pr = L, nex = pr - next，而在输入第一个数时，nex就是NULL，需要进行单独处理，不能放在后面的循环取pre，因为NULL哪里有pre

void HeadCreat_De_LinkList(De_LinkList &L, int len){
    LNode *pr, *cnt, *nex;//pr是前一个节点，也就是头节点，cnt是新来的节点，nex是头节点后面的节点
    pr = L;
    cnt = (LNode*)malloc(sizeof(LNode));
    cin>>cnt->val;//输入新节点的值
    cnt->next = NULL;//对一个点进行特殊处理，他后面是没有元素的，所以给next赋值为NULL
    cnt->pre = L;//赋pre为头指针
    L->next = cnt;//更新头指针的next指针
//用s保存cnt，就是第一个输入的元素，也就是链表的尾节点，便于倒序输出
//LNode *s;
//s = cnt;
    for(int i = 2; i <= len; ++i){//循环从2开始
        cnt = (LNode*)malloc(sizeof(LNode));//开辟空间
        cin>>cnt->val;//输入数据
      //给pr和nex赋值
        pr = L;
      	nex = L->next;
      //再就是四步曲，见图上面的文字
        cnt->next = nex;、
        nex->pre = cnt;
        cnt->pre = pr;
        pr->next = cnt;
    }
//从后往前输出，用于检查pre是否好用
//  while (s->pre != NULL) {
//        cout<<s->val<<' ';
//        s = s->pre;
//    }
//    cout<<endl;
}

尾插法创建双向链表

尾插法比头插法容易实现，他不需要pre，nex，只需要一个链表的尾节点tail，然后对每个新来的点，直接插到tail后面去即可

void TailCreat_De_LinkList(De_LinkList &L, int len){
    LNode *s, *tail;//s是辅助节点，用来存新来的节点，tail是链表的尾节点
    tail = L;//最开始的时候尾节点就是头节点
    for(int i = 1; i <= len; ++i){
        s = (LNode*)malloc(sizeof(LNode));//申请空间
        cin>>s->val;//输入值
        tail->next = s;//直接让尾节点的next指向新节点
        s->pre = tail;//让新节点的pre指向尾节点
        tail = s;//因为是尾插，所以尾节点改变了，就要时时更新
    }
    tail->next = NULL;
//下面是检测代码，是从后往前遍历，证明pre是可以用滴
//    while (tail->pre != NULL) {
//        cout<<tail->val<<' ';
//        tail = tail->pre;
//    }
//    cout<<endl;
}

插入元素

void Insert_De_LinkList(De_LinkList &L, int pos, int val){
    LNode *pr, *cnt, *nex;//和头插法一样
    pr = L;
    int j = 1;
    while (pr != NULL && j < pos) {//找到pos前一个位置
        pr = pr->next;
        ++j;
    }
    nex = pr->next;//nex是pos节点
    cnt = (LNode*)malloc(sizeof(LNode));//开辟空间
    cnt->val = val;//赋新节点值
  //四步走，见头插法
    cnt->next = nex;
    nex->pre = cnt;
    cnt->pre = pr;
    pr->next = cnt;   
}

删除元素

void Delet_De_LinkList(De_LinkList &L, int pos){
    LNode *cnt, *pr, *nex;//和头插法差不多
    pr = L;
    int j = 1;
    while (pr != NULL && j < pos) {//pr指向pos的前一个节点
        ++j;
        pr = pr->next;
    }
    cnt = pr->next;//cnt指向pos节点
    nex = cnt->next;//nex指向pos的下一个节点
    if(nex != NULL){//如果删除的不是最后一个元素
        pr->next = nex;//让pr的next指向nex，也就是让pos前节点的next指向pos的后节点
        nex->pre = pr;//让nex的pre节点指向pr，也就是让pos的后节点的pre指向pos的前节点
    }
    else {//如果是最后一个元素，那么nex就是NULL，此时只需要让pr的next指针指向NULL即可
        pr->next = nex;
    }
}

打印列表

void Print_De_LinkList(De_LinkList L){
    LNode *p;
    p = L ->next;
    while (p !=NULL) {
        cout<<p->val<<' ';
        p = p->next;
    }
    cout<<endl;
}

代码总览

#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using  namespace std;
#define inf 0x3f3f3f3f
#define MAX 10000 + 50
#define endl '
'
//#define mod 1000000007
//const int mod = 1e9 + 7;
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
//不开longlong见祖宗！
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

typedef struct LNode{
    int val;
    struct LNode *next, *pre;
}LNode, *De_LinkList;

void Init_De_LinkList(De_LinkList &L){
    L = (De_LinkList)malloc(sizeof(LNode));
    L->next = NULL;
    L->pre = NULL;
}

void HeadCreat_De_LinkList(De_LinkList &L, int len){
    LNode *pr, *cnt, *nex, *s;
    pr = L;
    cnt = (LNode*)malloc(sizeof(LNode));
    cin>>cnt->val;
    cnt->next = NULL;
    cnt->pre = L;
    L->next = cnt;
    s = cnt;
    for(int i = 2; i <= len; ++i){
        cnt = (LNode*)malloc(sizeof(LNode));
        cin>>cnt->val;
        pr = L;nex = L->next;
        cnt->next = nex;
        nex->pre = cnt;
        cnt->pre = pr;
        pr->next = cnt;
    }
//    while (s->pre != NULL) {
//        cout<<s->val<<' ';
//        s = s->pre;
//    }
//    cout<<endl;
}

void TailCreat_De_LinkList(De_LinkList &L, int len){
    LNode *s, *tail;
    tail = L;
    for(int i = 1; i <= len; ++i){
        s = (LNode*)malloc(sizeof(LNode));
        cin>>s->val;
        tail->next = s;
        s->pre = tail;
        tail = s;
    }
    tail->next = NULL;
//    while (tail->pre != NULL) {
//        cout<<tail->val<<' ';
//        tail = tail->pre;
//    }
//    cout<<endl;
}

void Insert_De_LinkList(De_LinkList &L, int pos, int val){
    LNode *pr, *cnt, *nex;
    pr = L;
    int j = 1;
    while (pr != NULL && j < pos) {
        pr = pr->next;
        ++j;
    }
    nex = pr->next;
    cnt = (LNode*)malloc(sizeof(LNode));
    cnt->val = val;
    cnt->next = nex;
    nex->pre = cnt;
    cnt->pre = pr;
    pr->next = cnt;

}

void Delet_De_LinkList(De_LinkList &L, int pos){
    LNode *cnt, *pr, *nex;
    pr = L;
    int j = 1;
    while (pr != NULL && j < pos) {
        ++j;
        pr = pr->next;
    }
    cnt = pr->next;
    nex = cnt->next;
    if(nex != NULL){
        pr->next = nex;
        nex->pre = pr;
    }
    else {
        pr->next = nex;
    }
}

void Print_De_LinkList(De_LinkList L){
    LNode *p;
    p = L ->next;
    while (p !=NULL) {
        cout<<p->val<<' ';
        p = p->next;
    }
    cout<<endl;
}



int main(){
    int n;
    De_LinkList L;

    cin>>n;
    Init_De_LinkList(L);
    HeadCreat_De_LinkList(L, n);
    Print_De_LinkList(L);
    
    cin>>n;
    Init_De_LinkList(L);
    TailCreat_De_LinkList(L, n);
    Print_De_LinkList(L);
    
    int pos, val;
    cin>>pos>>val;
    Insert_De_LinkList(L, pos, val);
    Print_De_LinkList(L);
    
    cin>>pos;
    Delet_De_LinkList(L, pos);
    Print_De_LinkList(L);
    return 0;
}

循环链表

循环链表和链表差不多，只需要将尾节点指向头节点即可，这里我通过实现约瑟夫环和抓兔子这个两个经典的循环链表问题来展示循环链表是如何实现的

约瑟夫环问题：

设有n个人围坐在圆桌周围，现从某个位置m(1≤m≤n)上的人开始报数，报数到k的人就站出来。下一个人，即原来的第k+1个位置上的人，又从1开始报数，再报数到k的人站出来。依次重复下去，直到全部的人都站出来为止。试设计一个程序求出这n个人的出列顺序。

因为此问题需要不断循环链表，并利用点的位置，所以头节点很碍事，索性就不要原来那种没有值的头节点，让第一个有值的节点成为头节点

采用尾插法

#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using  namespace std;
#define inf 0x3f3f3f3f
#define MAX 10000 + 50
#define endl '
'
//#define mod 1000000007
//const int mod = 1e9 + 7;
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
//不开longlong见祖宗！
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

typedef struct LNode {
    int data;
    struct LNode *next;
}LNode, *CLinkList;

void Init_CLinkList(CLinkList &L){//初始化
    L = (CLinkList)malloc(sizeof(LNode));
    L->next = L;
}

void Tail_CLinkList(CLinkList &L, int len){//无头节点的尾插法
    LNode *s, *tail;//辅助节点
    L->data = 1;//对头节点单独处理
    L->next = L;//next指针指向本身，形成循环，
    tail = L;
    for(int i = 2; i <= len; ++i){
        s = (LNode*)malloc(sizeof(LNode));
        s->data = i;//按题意赋值
        s->next = L;//尾插法，故让输入的节点的next指向第一个节点
        tail->next = s;//原来的尾节点指向新来的节点
        tail = s;//将新来的节点变成尾节点
    }
}

void Prinit_CLinkList(CLinkList L){//打印循环链表
    LNode *s = L ->next ;
    cout<<L->data<<' ';//先输出头节点，不然下面的循环的条件就写不了
    while (s != L){//循环结束条件都是根据你的链表的写法而定的
        cout<<s->data<<' ';
        s = s->next;
    }
    cout<<endl;
}

void YSF(CLinkList &L, int n, int m, int k){//约瑟夫环
    int j = 1;//计数，找到m-1的位置
    LNode *s, *p;//辅助节点，s用于约瑟夫环的循环，p用于找m节点的位置
    if(m == 1){//如果m=1，也就是第一个位置，就直接让p=L，不然也是下面的循环条件没法写
        p = L;
    }
    else p = L->next;
    while (j < m && p != L) {//找到位置m，此时p节点就是m的位置
        ++j;
        p = p->next;
    }
    cout<<"链表为 ";
    Prinit_CLinkList(L);
    cout<<"起点为 "<<p->data<<endl;//输出起点
    s = p;
    cout<<"出队顺序为：";
    while (s->next != s) {//当链表只剩下一个节点时结束循环，此时s节点的next指向他本身，这就是结束条件
        int sum = 1;//计数，看看到没到k
        while (sum < k - 1) {//结束之时，sum=k-1，s节点是需要删除的节点的前一个节点
            ++sum;
            s = s->next;
        }
        p = s->next;//p就是我们要删掉的节点
        cout<<p->data<<" -> ";//输出p的值
        s->next = p->next;//删掉p
        s = s->next;
    }
    cout<<s->data<<endl;//输出最后一个元素
}

int main(){
    CLinkList L;
    Init_CLinkList(L);
    int n, m, k;
    cin>>n;
    Tail_CLinkList(L, n);
    cin>>m>>k;
    YSF(L, n, m, k);
 		return 0;  
}

抓兔子

围绕着山顶有10个圆形排列的洞,互利要吃兔子,兔子说:”可以,但必须找到我,我就藏于这10个洞中,你先到1号洞找,第二次隔1个洞(即3号洞)找,第二次隔2个洞(即6号洞)找,以后如此类推,次数不限.”但狐狸从早到晚进进出出了1000次,仍没有找到兔子.问:兔子究竟藏在那个洞里，

同样是循环对列，操作和上面差不多都

#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using  namespace std;
#define inf 0x3f3f3f3f
#define MAX 10000 + 50
#define endl '
'
//#define mod 1000000007
//const int mod = 1e9 + 7;
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
//不开longlong见祖宗！
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
typedef struct LNode{
    int data;
    struct LNode *next;
}LNode, *CLinkList;

void Init_CLinkList(CLinkList &L){//同样是初始化
    L = (CLinkList)malloc(sizeof(LNode));
    L->next = L;
}

void TailCreat_CLinkList(CLinkList &L, int n){//同样的尾插法建立循环链表
    L->data = 1;//先特殊处理第一个节点
    LNode *s, *tail;
    tail = L;//因为只有一个节点，所以即是头节点又是尾节点
    for(int i = 2; i <= n; ++i){
        s = (LNode*)malloc(sizeof(LNode));
        s->data = i;
        tail->next = s;
        s->next = L;
        tail = s;
    }
}

void Print_CLinkList(CLinkList &L){//打印链表，同上
    LNode *s;
    s = L;
    cout<<s->data<<' ';
    s = L->next;
    while (s != L) {
        cout<<s->data<<' ';
        s = s->next;
    }
    cout<<endl;
}

void f(CLinkList L,int n, int k){//开始抓兔子辽
    bool vis[n + 1];//标记数组，用力记录这个点有没有来过
    mem(vis, 0);//清0是个好习惯
    int num = 1, pos = 1, cnt = 2;//num表示本次需要在第几个坑（即1，3，6，10等等），pos是当前的位置，cnt表示每次num找到后需要重新增加的值
    cout<<"链表为： ";
    Print_CLinkList(L);//打印链表
    cout<<"抓兔子的过程为：";

    LNode *s;
    s = L;
    while (k--) {//找k此
        while (pos < num) {//找到num的位置
            ++pos;
            s = s->next;
        }
        cout<<s->data<<" -> ";
        vis[s->data] = 1;//标记这个点已经来过
        num += cnt;//更新num值
        ++cnt;//更新cnt值
    }
    cout<<"兔子可能的藏身之处 ";
    for(int i = 1; i <= n; ++i){
        if(!vis[i])cout<<i<<' ';//没标记过即没来过
    }
}

int main(){
    int n, k;
    cin>>n>>k;
    CLinkList L;
    Init_CLinkList(L);
    TailCreat_CLinkList(L, n);
    f(L, n, k);
    return 0;
}

总结：

链表其实没那么难搞，写来写去就那几个函数，搞明白next、pre、边界等小地方就没问题辽，最重要的是要搞清楚单链表的各种操作，多码几遍，然后你就会发现其他的什么双向链表、循环链表、循环双向链表等等都是小儿科o(︶︿︶)o