有些背包都是需要求方案具体是什么的,于是问问dalao,有道01背包求方案数的题,卡了好久。

求背包的方案数,这个问题就很好了,我不会qwq。
搞了半天是先存方案于是在背包更新的时候就存下方案吧,发现存不了因为状态在不停的被更新于是采取一种方法。
找到输入的时候先从n到1输入,背包的时候从1开始这样就可以保证第一个物品最后一个更新f数组了。最后找到最优解顺序递推推出答案。

#include<iostream> #include<cstdio> #include<cstring> #include<ctime> #include<string> #include<cmath> #include<algorithm> #include<iomanip> #include<map> #include<queue> #include<stack> #include<vector> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int maxn=1000; int f[maxn][maxn],w[maxn],v[maxn],c[maxn],x,y,ans=0; int n,m,u; int main() { //freopen("1.in","r",stdin); memset(f,0xcf,sizeof(f)); m=read();u=read();n=read(); f[0][0]=0; for(int i=n;i>=1;i--){w[i]=read();c[i]=read();v[i]=read();} for(int i=1;i<=n;i++) { for(int j=m;j>=w[i];j--) { for(int k=u;k>=c[i];k--) { f[j][k]=max(f[j][k],f[j-w[i]][k-c[i]]+v[i]); if(ans<f[j][k]){ans=f[j][k];x=j;y=k;} } } } printf("%d ",ans); for(int i=n;i>=1;i--) { if(x>=w[i]&&y>=c[i]) if(f[x][y]==f[x-w[i]][y-c[i]]+v[i]) { printf("%d ",n-i+1); x-=w[i];y-=c[i]; } } return 0; }
必须要给数组取0xcf(负无穷),因为你的最优解虽然在f[n][m]之中但是呢,从后往前推答案的时候必须要找到你最后一个物品更新后的最优解的位置否则就是你的背包没被装满就开始更新你的方案的,这很大程度是错误的所以必须找到背包被刚好装满的那个n,m;代码就是这样。
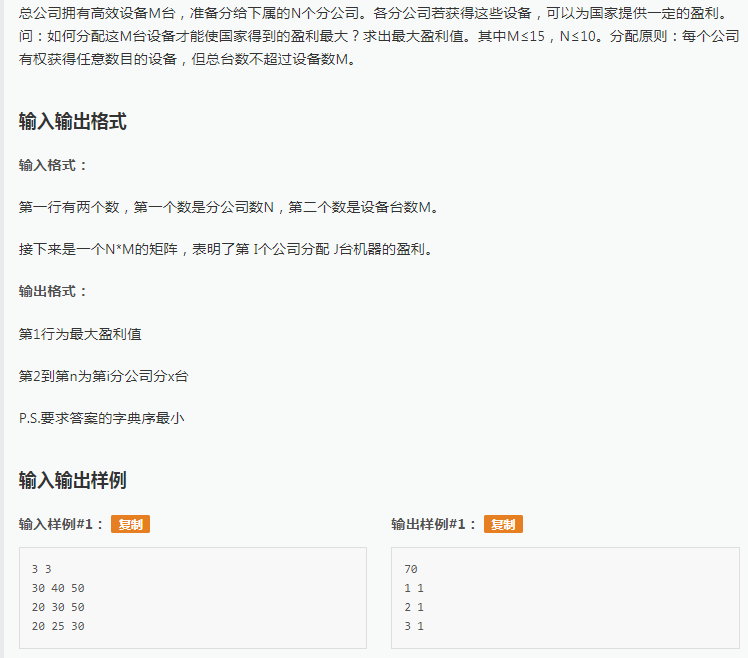
这道题也要输出分给其他公司的机器号,要求字典序最小,所以尽可能的让前面的机器少,这样可以使字典序最小.例如第一个公司分配机器数为0,这就是最优的第一个机器分配方案的第一步。
考虑记录路径每次更新都更新路径,开一个三维数组path[i][j][i]表示第j台机器分给第i个公司后第i个公司分到的机器数量
if(f[i][j]<=f[i-1][j-k]+a[i][k])
{
f[i][j]=f[i-1][j-k]+a[i][k];
for(int h=1;h<i;h++)
{
path[i][j][h]=path[i-1][j-k][h];
}
path[i][j][i]=k;
}
这样每次都记录一下路径,注意if(f[i][j]<=f[i-1][j-k]+a[i][k])这个是<=意思是如果后面的能更新当前的尽管和当前的最优解相等也要进行更新这样可以是答案是字典序。这样就可以完美的ac这道题了。

#include<iostream> #include<cstdio> #include<map> #include<vector> #include<iomanip> #include<cmath> #include<ctime> #include<cstring> #include<string> #include<algorithm> #include<queue> #include<stack> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int n,m; int a[102][102],f[102][102];//设f[i][j]表示第j个机器给到第i个公司的最大利益。 int path[20][20][20]; int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=read(); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) for(int k=0;k<=j;k++) { if(f[i][j]<=f[i-1][j-k]+a[i][k]) { f[i][j]=f[i-1][j-k]+a[i][k]; for(int h=1;h<i;h++) { path[i][j][h]=path[i-1][j-k][h]; } path[i][j][i]=k; } } printf("%d ",f[n][m]); for(int i=1;i<=n;i++)printf("%d %d ",i,path[n][m][i]); return 0; }
发生过一次的事情,有可能不会再发生,发生过两次的事情就一定会发生第三次。
