10 10

今天的题目还行..

今天得分 300.

 

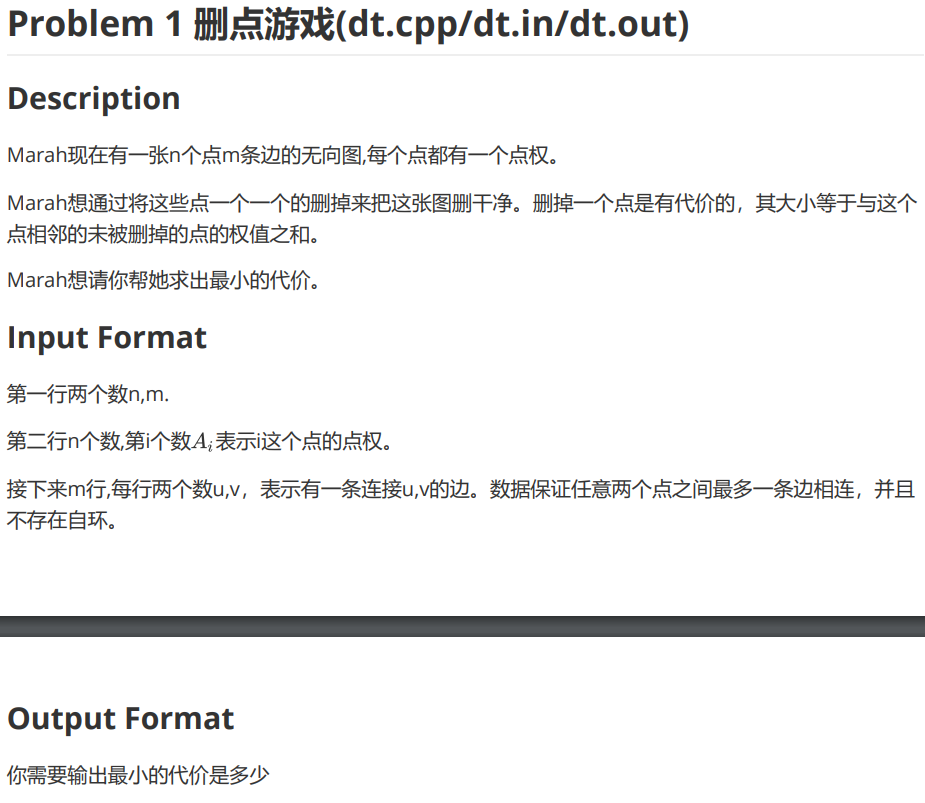
这道题很难了 我想了1个半小时。对于30显然爆搜一下。对于100分 考虑dp 发现没什么好dp的 所以就贪心好了。

考虑怎么贪心我是没有考虑到最小点权的一些关键所以 设了两个数组 wx 表示x这个点的想要删掉的代价 bx表示x 这个点对其他点造成的影响。

花了几个例子发现 wx-bx先删掉最小那个比较不错 但是每次删掉一个点 wx 和 bx都是要被更新的 考虑用堆维护并不好搞所以考虑开线段树。

因为这个结论我也不知道是对是错所以先码了线段树 但是没有过大样例 当时过去1h了有点慌。

//#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)>(y)?(y):(x))
#define INF 10000000000000000ll
#define ll long long
#define db double
#define mod 1000000007
#define l(p) t[p].l
#define r(p) t[p].r
#define v(p) t[p].v
#define id(p) t[p].id
#define zz p<<1
#define yy p<<1|1
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
const int MAXN=100010;
int n,m,len;
int lin[MAXN],nex[MAXN<<1],ver[MAXN<<1],vis[MAXN];
ll w[MAXN],a[MAXN],b[MAXN],ans;
struct wy
{
    int l,r;
    ll v;
    int id;
}t[MAXN];
inline void add(int x,int y)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
}
inline void build(int p,int l,int r)
{
    l(p)=l;r(p)=r;
    if(l==r){v(p)=w[l]-a[l]*b[l];id(p)=l;return;}
    int mid=(l+r)>>1;
    build(zz,l,mid);
    build(yy,mid+1,r);
    id(p)=v(zz)<v(yy)?id(zz):id(yy);
    v(p)=min(v(zz),v(yy));
}
inline void change(int p,int x,ll v)
{
    if(l(p)==r(p)){v(p)=v;return;}
    int mid=(l(p)+r(p))>>1;
    if(x<=mid)change(zz,x,v);
    else change(yy,x,v);
    id(p)=v(zz)<v(yy)?id(zz):id(yy);
    v(p)=min(v(zz),v(yy));
}
int main()
{
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
    n=read();m=read();
    for(int i=1;i<=n;++i)a[i]=read();
    for(int i=1;i<=m;++i)
    {
        int x,y;
        x=read();y=read();
        add(x,y);add(y,x);
        ++b[x];++b[y];
        w[x]+=a[y];w[y]+=a[x];
    }
    build(1,1,n);
    for(int i=1;i<=n;++i)
    {
        int x=id(1);
        //if(i==n)cout<<v(1)<<endl;
        //if(vis[x])cout<<"www"<<endl;
        ans+=w[x];vis[x]=1;
        change(1,x,INF);
        for(int j=lin[x];j;j=nex[j])
        {
            int tn=ver[j];
            if(vis[tn])continue;
            --b[tn];
            w[tn]-=a[x];
            change(1,tn,w[tn]-a[tn]*b[tn]);
        }
    }
    printf("%lld
",ans);
    return 0;
}

想了一下 应该是贪心策略出现了问题。考虑写个爆搜 来水30分。

//#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)>(y)?(y):(x))
#define INF 10000000000000000ll
#define ll long long
#define db double
#define mod 1000000007
#define l(p) t[p].l
#define r(p) t[p].r
#define v(p) t[p].v
#define id(p) t[p].id
#define zz p<<1
#define yy p<<1|1
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
const int MAXN=100010;
int n,m,len;
int lin[MAXN],nex[MAXN<<1],ver[MAXN<<1],vis[MAXN];
ll w[MAXN],a[MAXN],b[MAXN],ans=INF;
struct wy
{
    int l,r;
    ll v;
    int id;
}t[MAXN];
inline void add(int x,int y)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
}
inline void dfs(int x,int v)
{
    if(x==n+1)
    {
        ans=min(ans,v);
        return;
    }
    for(int i=1;i<=n;++i)
    {
        if(vis[i])continue;
        vis[i]=1;
        for(int j=lin[i];j;j=nex[j])
        {
            int tn=ver[j];
            //if(vis[tn])continue;
            w[tn]-=a[i];
        }
        dfs(x+1,v+w[i]);
        vis[i]=0;
        for(int j=lin[i];j;j=nex[j])
        {
            int tn=ver[j];
            //if(vis[tn])continue;
            w[tn]+=a[i];
        }
    }
}
int main()
{
    freopen("1.in","r",stdin);
    freopen("2.out","w",stdout);
    n=read();m=read();
    for(int i=1;i<=n;++i)a[i]=read();
    for(int i=1;i<=m;++i)
    {
        int x,y;
        x=read();y=read();
        add(x,y);add(y,x);
        ++b[x];++b[y];
        w[x]+=a[y];w[y]+=a[x];
    }
    dfs(1,0);
    printf("%lld
",ans);
    return 0;
}

考虑推出正确贪心策略 所以开始对拍 排出几组非常小的数据点把自己的线段树给卡掉了。

//#include<bits/stdc++.h>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<queue>
#include<deque>
#include<vector>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#include<cstdlib>
using namespace std;
const int MAXN=10010;
int maxx=510;
int maxx1=100;
int n,m,T;
int a[MAXN][MAXN];
int main()
{
    freopen("1.in","w",stdout);
    srand(time(0));
    n=rand()%5+1;m=min(max(0,(n*(n-3)/2))%5+1,n*(n-1)/2);
    cout<<n<<' '<<m<<endl; 
    for(int i=1;i<=n;++i)cout<<rand()%20+1<<' ';
    cout<<endl;
    for(int i=1;i<=m;++i)
    {
        int x=rand()%n+1,y=rand()%n+1;
        while(x==y||a[x][y]||a[y][x])
        {
            x=rand()%n+1,y=rand()%n+1;
        }
        a[x][y]=1;
        cout<<x<<' '<<y<<endl;
    }
    return 0;
}

手玩数据发现了一些性质每次删点代价都是 和自己相连的代价比自己小的代价和。既然是这样 那么对于每一条边处理一下 取min(a[x],a[y]) 的累和即可。成功推出来结论。

//#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)>(y)?(y):(x))
#define INF 10000000000000000ll
#define ll long long
#define db double
#define mod 1000000007
#define l(p) t[p].l
#define r(p) t[p].r
#define v(p) t[p].v
#define id(p) t[p].id
#define zz p<<1
#define yy p<<1|1
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
const int MAXN=100010;
int n,m,len;
ll a[MAXN],ans;
int main()
{
    freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<=n;++i)a[i]=read();
    for(int i=1;i<=m;++i)
    {
        int x,y;
        x=read();y=read();
        ans+=min(a[x],a[y]);
    }
    printf("%lld
",ans);
    return 0;
}

当时时间不够没有证明这里可以证明一下 构造一种方案使得代价最小其实我们发现对于一条边我们需要付出的代价是 a[x] a[y] 显然上述做法是最优的。考虑有没有一种情况是无法每次都是取min(a[x],a[y])的。

只要构造出来一种方案使得我们每次都是可以取min(a[x],a[y])这种方案的就可以证明结论了。有一种构造方法是这样的：考虑全局代价最小的点，我们先将其删掉然后发现对于和其相连的边 都取到了min

然后再找全局最小值再删掉 这样就构造出来了上述结果。所以结论成立。

这道题是很有意思 初看没有任何算法的气息 然后感觉能二分尽量二分吧 观察题目是从起点走到菜场 求最短路径下的最大体格之和。

先假设只有一个菜场我们发现bfs 然后在bfs中dp一下就好了因为bfs保证了最短路径。考虑这个dp怎么做我们必须求出每个点能拥有的体格大小。

这个显然是正方形 所以考虑从每个点开始向上向下向左向右扫 但是这样复杂度是n^2m^2这都T了..因为每次都是正方形。

所以考虑dp f[i][j] 表示以i j这个点为基准左上方的最大正方形，这个dp显然是nm的所以此时贡献就可以nms计算了。

dp其实 f[i][j] 表示到达这个点的最大体格之和 转移只要是连贯的最短路转移即可。(因为这个我傻了转移10min才发现自己写错了。

考虑多个其实就和昨天的题目一样了考虑状压bfs 但是复杂度过高且有些状态无用所以考虑bfs预处理再状压。

注意预处理的时候起点和终点的代价不能算上最后统一累加否则将会在dp的时候计算重复 不好处理。

//#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)>(y)?(y):(x))
#define INF 1000000000
#define ll long long
#define db double
#define mod 1000000007
#define pii pair<int,int>
#define mk make_pair
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int MAXN=310,maxn=16;
const int dx[5]={0,1,-1,0,0};
const int dy[5]={0,0,0,1,-1};
int n,m,s,p,ans,cnt=INF,pp;
int st,en,maxx;
int a[MAXN][MAXN],f[MAXN][MAXN];
int g[maxn][1<<maxn],b[maxn][1<<maxn];
int c[MAXN][MAXN],v[MAXN][MAXN];//由某个点到某个点的最大价值
int w[MAXN][MAXN],vis[MAXN][MAXN],mark[MAXN][MAXN];
queue<pii> q;
struct wy
{
    int x,y;
}t[MAXN];
inline void prepare()
{
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j)
        {
            if(a[i][j]==1)continue;
            f[i][j]=min(f[i-1][j],min(f[i-1][j-1],f[i][j-1]))+1;
        }
}
inline void bfs()
{
    while(q.size())
    {
        int x=q.front().first;
        int y=q.front().second;
        f[x][y]+=w[x][y];
        q.pop();
        for(int i=1;i<=4;++i)
        {
            int xx=x+dx[i];
            int yy=y+dy[i];
            if(xx<1||yy<1||xx>n||yy>m)continue;
            if(a[xx][yy])continue;
            if(f[xx][yy]<f[x][y]&&vis[xx][yy]==vis[x][y]+1)
            {
                f[xx][yy]=f[x][y];
            }
            if(vis[xx][yy])continue;
            f[xx][yy]=f[x][y];
            vis[xx][yy]=vis[x][y]+1;
            q.push(mk(xx,yy));
        }
    }
}
inline void zb(int x,int y)
{
    q.push(mk(x,y));
    memset(vis,0,sizeof(vis));
    memset(f,-1,sizeof(f));
    vis[x][y]=1;f[x][y]=-w[x][y];
}
int main()
{
    //freopen("1.in","r",stdin);
    freopen("expand.in","r",stdin);
    freopen("expand.out","w",stdout);
    n=read();m=read();s=read();
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j)a[i][j]=read();
    st=read()+1;en=read()+1;p=read();
    maxx=(1<<p)-1;
    for(int i=1;i<=p;++i)
    {
        int x,y;
        x=read()+1;y=read()+1;
        t[i]=(wy){x,y};
    }
    prepare();
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=m;++j)
        {
            for(int k=0;k<=s;++k)
            {
                int ww=2*k+1;
                int half=ww/2;
                int x=i+half;
                int y=j+half;
                if(f[x][y]>=ww)w[i][j]=k;
                else break;
            }
        }
    }
    for(int i=1;i<=p;++i)
    {
        zb(t[i].x,t[i].y);
        bfs();
        pp+=w[t[i].x][t[i].y];
        for(int j=1;j<=p;++j)
        {
            if(i==j)continue;
            int x=t[j].x;
            int y=t[j].y;
            c[i][j]=vis[x][y]-1;
            v[i][j]=f[x][y]-w[x][y];
            //cout<<v[i][j]<<' ';
        }
        //cout<<endl;
    }
    zb(st,en);bfs();
    memset(g,0x3f,sizeof(g));
    for(int i=1;i<=p;++i)
    {
        g[i][1<<(i-1)]=vis[t[i].x][t[i].y]-1;
        b[i][1<<(i-1)]=f[t[i].x][t[i].y]-w[t[i].x][t[i].y]+w[st][en];
    }
    for(int j=1;j<maxx;++j)
    {
        for(int i=1;i<=p;++i)
        {
            if(!(j&(1<<(i-1))))continue;
            for(int k=1;k<=p;++k)
            {
                if((j&(1<<(k-1))))continue;
                int ss=j|(1<<(k-1));
                if(g[k][ss]>g[i][j]+c[i][k])
                {
                    g[k][ss]=g[i][j]+c[i][k];
                    b[k][ss]=b[i][j]+v[i][k];
                }
                else
                {
                    if(g[k][ss]==g[i][j]+c[i][k])
                    {
                        b[k][ss]=max(b[k][ss],b[i][j]+v[i][k]);
                    }
                }
            }
        }
    }
    for(int i=1;i<=p;++i)cnt=min(cnt,g[i][maxx]);
    for(int i=1;i<=p;++i)if(g[i][maxx]==cnt)ans=max(ans,b[i][maxx]);
    printf("%d %d
",cnt,ans+pp);
    return 0;
}

考试的时候由于很紧张所以非常认真所以调试的时候也没遇到什么困难。

这道题就比较有内涵了 每次都考这种知识点 和图论嵌套的dp 题目。

显然有状态是 f[x][j]从某点出发到达点x 此时最大公约数为j的最小代价。 转移很好写因为j已知。

也发现了整张图类似于分层图且f数组已经完成分层这种形式了 且整张图边权>=1所以 dij直接跑起。优化加起来。

所以这道题 我以 1000*1000*500*logn+一堆感觉能跑的很快的剪枝和优化跑过了。

//#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)>(y)?(y):(x))
#define INF 1000000000
#define ll long long
#define db double
#define mod 1000000007
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
const int MAXN=2010,maxn=520;
int n,m,len,Q,maxx,ans;
int g[maxn][maxn],cnt[MAXN],mark[MAXN];
int lin[MAXN],ver[MAXN<<1],nex[MAXN<<1],e[MAXN<<1];
inline void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
inline int gcd(int a,int b){return b?gcd(b,a%b):a;}
int f[MAXN][maxn],vis[MAXN][maxn];
struct wy
{
    int g,x,v;
    int friend operator <(wy a,wy b){return a.v>b.v;}
};
priority_queue<wy> q;
inline void dij()
{
    while(q.size())
    {
            wy w=q.top();
            q.pop();
        if(w.x==n)ans=min(ans,w.v);
        if(w.v>=ans)continue;
        if(vis[w.x][w.g])continue;
        vis[w.x][w.g]=1;
        for(int i=lin[w.x];i;i=nex[i])
        {
            int tn=ver[i];
            int zz=e[i]/g[e[i]][w.g];
            int gg=g[e[i]][w.g];
            if(f[tn][gg]>f[w.x][w.g]+zz)
            {
                f[tn][gg]=f[w.x][w.g]+zz;
                q.push((wy){gg,tn,f[tn][gg]});
            }
        }
    }
}
int main()
{
    //freopen("1.in","r",stdin);
    freopen("magic.in","r",stdin);
    freopen("magic.out","w",stdout);
    n=read();m=read();
    for(int i=1;i<=m;++i)
    {
        int x,y,z;
        x=read();y=read();z=read();
        maxx=max(maxx,z);
        add(x,y,z);add(y,x,z);
    }
    for(int i=0;i<=maxx;++i)
        for(int j=0;j<=maxx;++j)
            g[i][j]=gcd(i,j);
    Q=read();
    for(int i=1;i<=Q;++i)
    {
        int x=read();
        if(mark[x]){printf("%d
",cnt[x]);continue;}
        memset(f,0x3f,sizeof(f));
        memset(vis,0,sizeof(vis));
        f[x][0]=0;
        q.push((wy){0,x,0});
        ans=INF;dij();
        cnt[x]=ans;mark[x]=1;
        printf("%d
",ans);
    }
    return 0;
}

但是这显然 不够优秀也 在复杂度上感觉是通不过这道题目的 考虑优化这个算法。发现瓶颈在于每个点都要跑一次。

但是终点只有一个 我们从终点倒着跑到每个点这样应该就可以只跑一次了。考虑状态 f[i][j] 表示 到了第i个点到第n个点此时最大公约数为j的最短距离。

那么转移就很显然了 但是我们需要枚举的是上一次的最大公约数是谁 因为上一次的状态是未知的 转移即可。

这里有一个小detail ：设当前边的 权值为w 当前gcd 为g 生成的 gcd 为 g1 可能存在 gcd(g1,w)>g 的情况 权值还能更小 但此时 这个转移看似是不合法的 其实是不必要纠结的 因为存在 g被转移过来之后 g1 也一定会被转移过来且此时答案一定不会更差所以一定存在g1的出队 所以尽管这里是不合法的 也是可以进行随便转移的。

总复杂度 由于是dij 所以每个状态出队一次 每次出队的状态都会 枚举倍数一次 所以复杂度为n*w*logw*logn==5*10^6*logn 很稳了。其中w为边权的最大值.

然后就可以O(1) 回答询问了。

//#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)>(y)?(y):(x))
#define INF 1000000000
#define ll long long
#define db double
#define mod 1000000007
#define pii pair<int,int>
#define mk make_pair
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    int x=0,f=1;char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
const int MAXN=2010,maxn=520;
int n,m,len,Q,maxx,ans;
int cnt[MAXN],mark[MAXN];
int f[MAXN][maxn],vis[MAXN][maxn];
int lin[MAXN],ver[MAXN<<1],nex[MAXN<<1],e[MAXN<<1];
inline void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
struct wy
{
    int g,x,v;
    int friend operator <(wy a,wy b){return a.v>b.v;}
};
priority_queue<wy> q;
inline void dij()
{
    while(q.size())
    {
        wy w=q.top();
        q.pop();
        if(vis[w.x][w.g])continue;
        vis[w.x][w.g]=1;
        for(int i=lin[w.x];i;i=nex[i])
        {
            int tn=ver[i];
            if(e[i]%w.g)continue;
            for(int j=w.g;j<=maxx;j+=w.g)
            {
                if(f[tn][j]>w.v+e[i]/w.g)
                {
                    f[tn][j]=w.v+e[i]/w.g;
                    q.push((wy){j,tn,f[tn][j]});
                }
            }
        }
    }
}
int main()
{
    freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<=m;++i)
    {
        int x,y,z;
        x=read();y=read();z=read();
        maxx=max(maxx,z);
        add(x,y,z);add(y,x,z);
    }
    memset(f,0x3f,sizeof(f));
    memset(cnt,0x3f,sizeof(cnt));
    for(int i=1;i<=maxx;++i)
    {
        f[n][i]=0;
        q.push((wy){i,n,0});
    }
    dij();
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=maxx;++j)
        cnt[i]=min(cnt[i],f[i][j]);
    }
    Q=read();
    for(int i=1;i<=Q;++i)
    {
        int x=read();
        printf("%d
",cnt[x]);
    }
    return 0;
}

快考试了 希望不要这么一直菜下去。