对于环形的dp 大多情况都是破环成链 例如 那道宝石手镯的环形 一般来说都是要破环成链的。
或者说 是 两次dp 一次断开 一次强制连接即可。
我想 我应该沉淀下来了这些天写的题都有点虚 要不就是看了书 要不就是点开了题解总是在自己未想出的时候 外物影响到我让我感觉特别没有成就感呢。
这就很不爽了 我觉得是真的不爽 ,算了按照原计划行事(oj刷上520)

这道题目 看起来很简单 我的意思是指 很轻而易举的列出来状态和 状态转移方程 事实上也是如此 。
但是唯一难以处理的是 环形的结构 。。我设状态 因为要知道前面那个到底选了没有所以必须要写两个选或不选的状态。
设 f[i][j][0/1] 表到了第i个小时已经形成j段且第i个小时选 0 不选 1。
f[1][1][0]=0; f[1][0][1]=0;
显然 f[i][j][0]=max(f[i-1][j-1][1],f[i-1][j-1][0]+v[j]); f[i][j][1]=max(f[i][j][0],f[i][j][1]);
对于环形的 上述我们断开dp一次了 此时为了弥补刚才断开的后果我们必须要连接上去。
此时状态必然是 f[1][1][0]=v[1]; 此时我们再进行上述dp 然后强制取答案 f[n][k][0]即可。
此时 B<n因为这道题保证了 那么在从一段数到最后的n一定有一个点会做铺垫。

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define ll long long #define R register #define mod 45989 using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline ll read() { ll x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(ll x) { x<0?putchar('-'),x=-x:0; ll num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar(' ');return; } const ll MAXN=4000; ll n,k,ans,u,cnt,minn=INF; ll v[MAXN]; ll f[2][MAXN][2]; inline ll min(ll x,ll y){return x>y?y:x;} inline ll max(ll x,ll y){return x>y?x:y;} //f[i][j][k] 表 前i个小时 分成了j段 且在第 i的小时休息 0 还是不休息 1 int main() { //freopen("1.in","r",stdin); n=read();k=read(); for(ll i=1;i<=n;++i)v[i]=read(); if(n==k){for(ll i=1;i<=n;++i)cnt+=v[i],minn=min(minn,v[i]);put(cnt-minn);} memset(f,0xcf,sizeof(f)); f[u][0][1]=0;f[u][1][0]=0; for(ll i=2;i<=n;++i) { u=u^1; for(ll j=0;j<=min(i,k);++j) { f[u][j][1]=-INF;f[u][j][0]=-INF; f[u][j][1]=max(f[u^1][j][0],f[u^1][j][1]); if(j-1>=0)f[u][j][0]=max(f[u^1][j-1][1],f[u^1][j-1][0]+v[i]); } } ans=max(ans,max(f[u][k][0],f[u][k][1])); u=0; memset(f,0xcf,sizeof(f)); f[u][1][0]=v[1]; for(ll i=2;i<=n;++i) { u=u^1; for(ll j=0;j<=min(i,k);++j) { f[u][j][1]=-INF;f[u][j][0]=-INF; f[u][j][1]=max(f[u^1][j][0],f[u^1][j][1]); if(j-1>=0)f[u][j][0]=max(f[u^1][j-1][1],f[u^1][j-1][0]+v[i]); } } ans=max(ans,f[u][k][0]); put(ans); return 0; }
一次断开 一次联合 强制联合 。这样即可消除环形带来的影响。
这样的做法当然还可以 用在创世纪上,当然我是不会的。
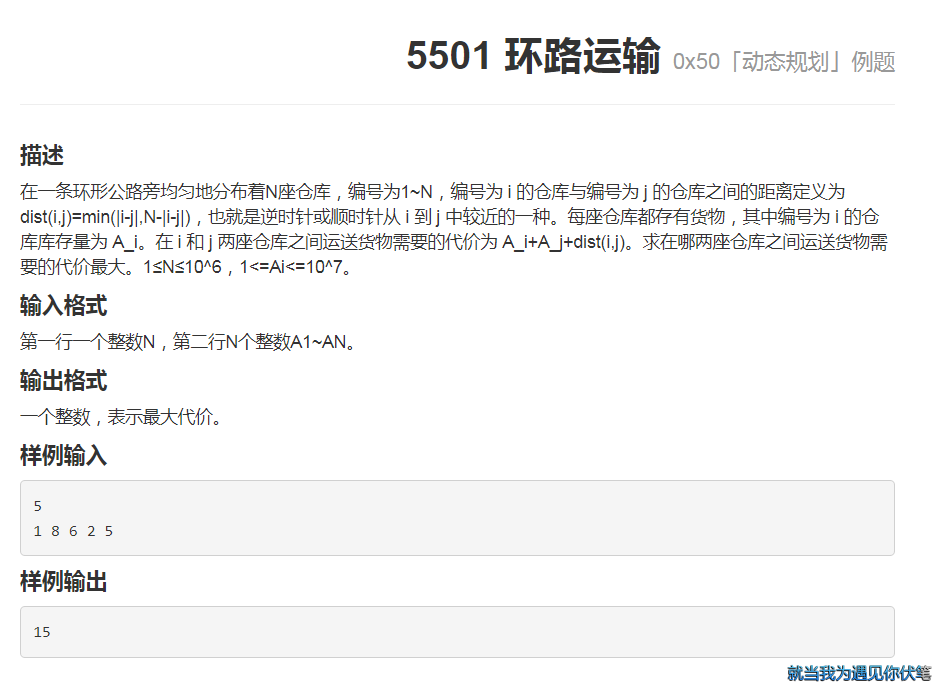
这道题的思路就比较简单了 n为le6 显然 也是一个dp类型的题目 瞬间单调队列O(1)寻找决策即可。
至于环形 考虑再续上一段 因为在这一段上两点之间的距离如果大于n/2的话那么此时再续上的一段两点之间的距离就小于了 这样我们就可以直接在这一条链上做了。
然后进行决策转移和决策单调性维护即可。

//#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<cstdlib> #include<cmath> #include<algorithm> #include<cctype> #include<utility> #include<set> #include<bitset> #include<queue> #include<stack> #include<deque> #include<map> #include<vector> #include<ctime> #define INF 2147483646 #define ll long long #define R register using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline ll read() { ll x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } inline void put(ll x) { x<0?putchar('-'),x=-x:0; ll num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; num==0?putchar('0'):0; while(num)putchar(ch[num--]); putchar(' ');return; } const ll MAXN=2000002; ll maxx,n; ll a[MAXN],q[MAXN],l,r; int main() { //freopen("1.in","r",stdin); n=read();l=1;r=0; for(ll i=1;i<=n;++i)a[i]=read(),a[i+n]=a[i]; for(ll i=1;i<=n+n/2;++i) { while(l<=r&&i-q[l]>n/2)++l; if(l<=r)maxx=max(maxx,a[i]+a[q[l]]+i-q[l]); while(l<=r&&a[q[r]]-q[r]<a[i]-i)--r; q[++r]=i; } put(maxx); return 0; }
