递归

递归简介

递归是一种解决问题的方法，将问题分解为更小的子问题，直到得到一个足够小的问题可以被很简单的解决，通常递归涉及函数调用自身。

递归三定律

1. 递归算法必须具有基本情况。
2. 递归算法必须改变其状态并向基本情况靠近。
3. 递归算法必须以递归方式调用自身。

举例

递归实现Fibonacci函数：

int FibonacciRecursive(int n)
{
    if( n < 2)
        return n;
    return (FibonacciRecursive(n-1)+FibonacciRecursive(n-2));
}

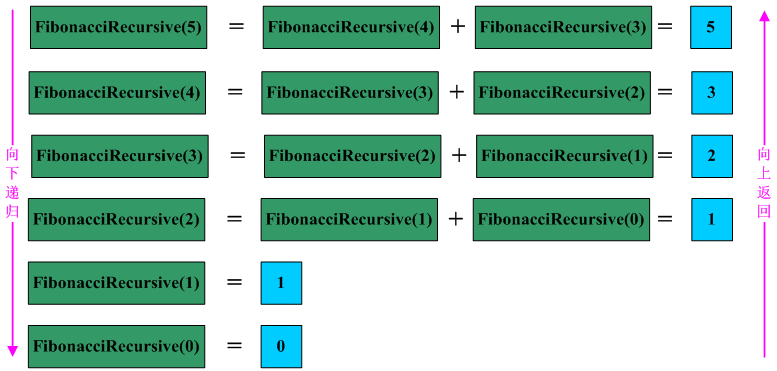
递归写的代码非常容易懂，完全是根据函数的条件进行选择计算机步骤。例如现在要计算n=5时的值，递归调用过程如下图所示：

尾递归

• 尾递归就是从最后开始计算, 每递归一次就算出相应的结果, 也就是说, 函数调用出现在调用者函数的尾部, 因为是尾部, 所以根本没有必要去保存任何局部变量。
• 尾递归就是把当前的运算结果（或路径）放在参数里传给下层函数，深层函数所面对的不是越来越简单的问题，而是越来越复杂的问题，因为参数里带有前面若干步的运算路径。
• 尾递归是极其重要的，不用尾递归，函数的堆栈耗用难以估量，需要保存很多中间函数的堆栈。

采用尾递归实现Fibonacci函数：

int FibonacciTailRecursive(int n,int ret1,int ret2)
{
   if(n==0)
      return ret1; 
    return FibonacciTailRecursive(n-1,ret2,ret1+ret2);
}

要计算n=5时的值，尾递归调用过程如下图所示：

从图可以看出，为递归不需要向上返回了，但是需要引入而外的两个空间来保持当前的结果。