辣鸡楼主之前高中空间几何马马虎虎，所以基础的几何知识就不会再阐述了
2D坐标系
1.2D笛卡尔坐标系较为简单就没mark了
2.2D极坐标
i.使用两个变量定义一个点到原点（极点）的距离r，方向θ（与X轴正方向夹角），这里有个注意点左手坐标系中顺时针方向角度为正，而右手坐标系中逆时针方向角度为负。
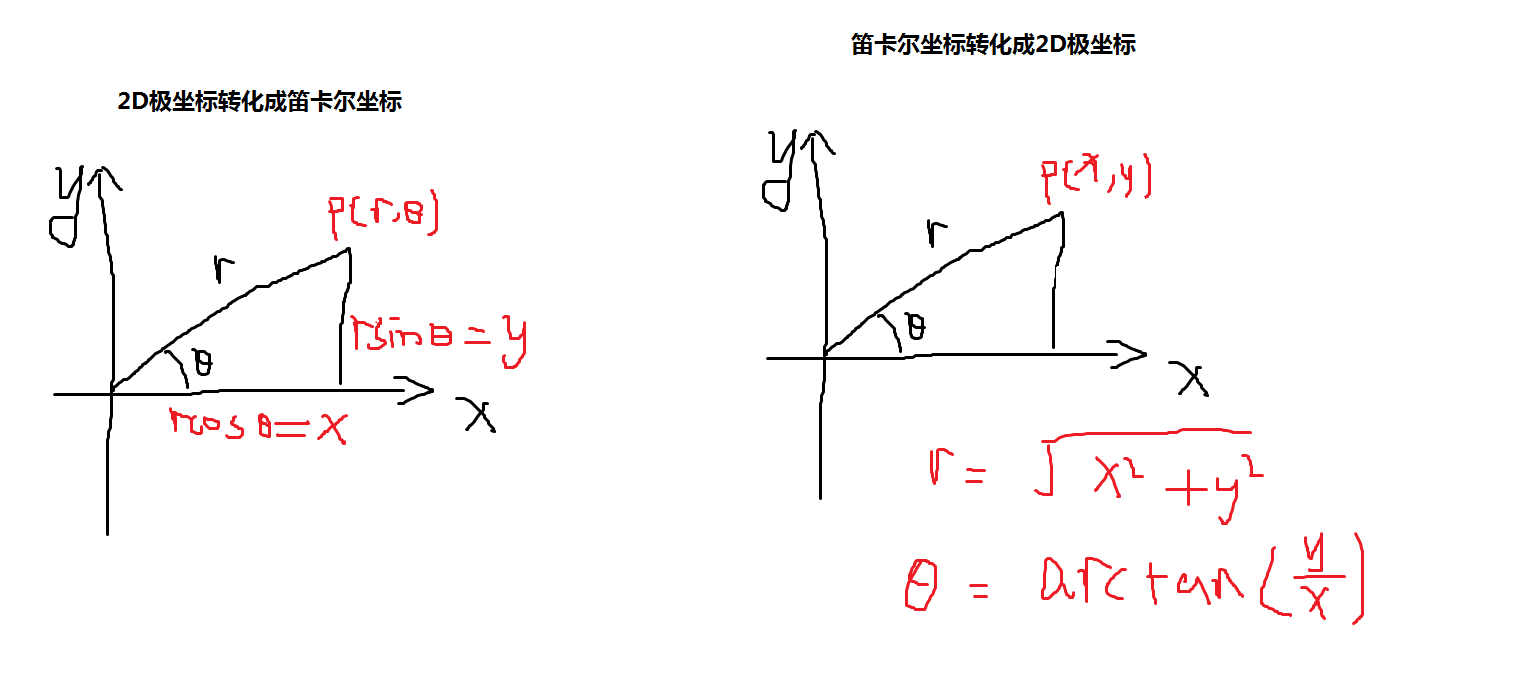右图θ可以使用arcsin或者arccos来计算
ii.主要应用：弹道，瞄准，导航方面
3D坐标系
1.3D笛卡尔也较为简单没mark
2.3D柱面坐标系
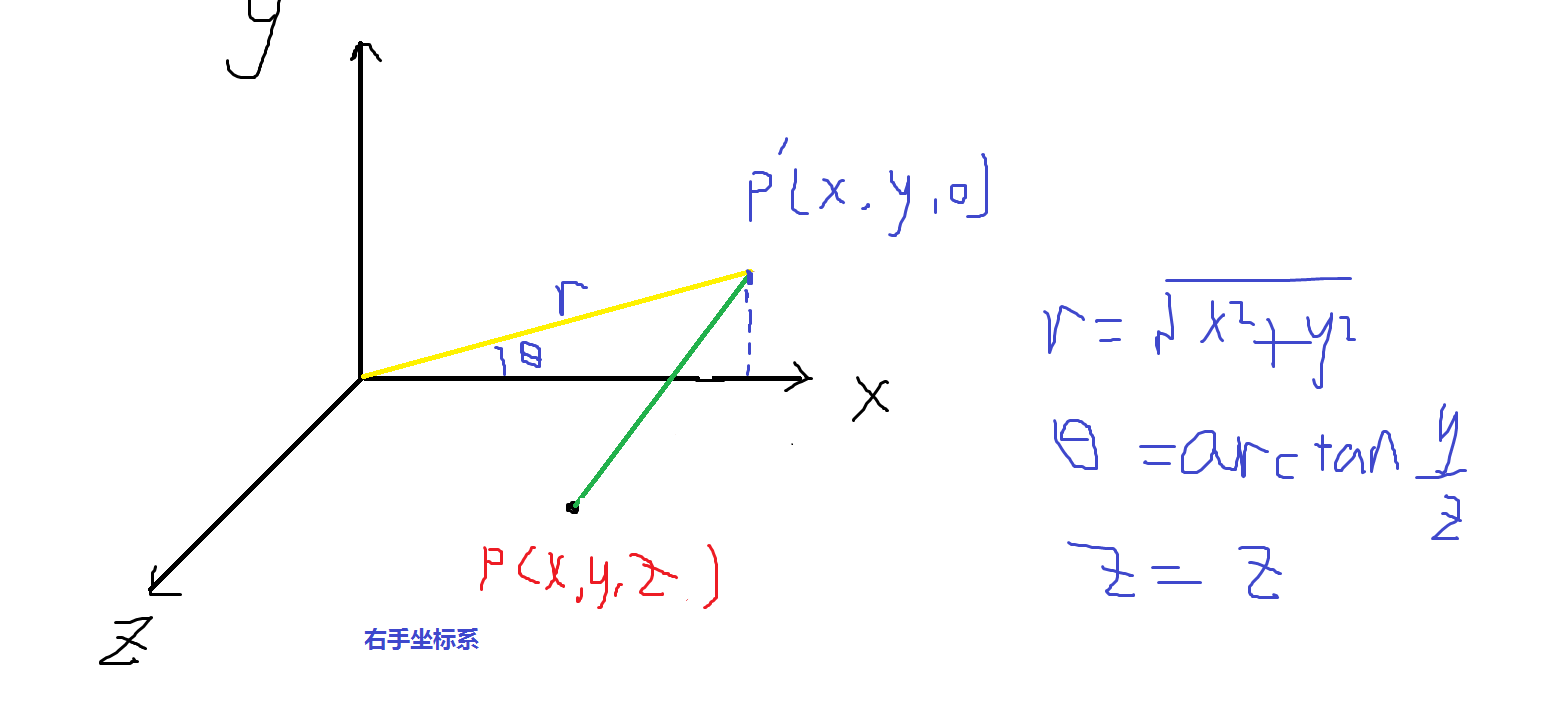
其实3D柱面坐标完全是由2D极坐标或者2D笛卡尔坐标转化而来，左图先根据2D极坐标知识确定p'点再往屏幕外平移z个单位即可，右图也同理
2.3D球面坐标系
用两个角度和到原点距离确定顶点P（ρ，Ø，θ）ρ为到原点距离
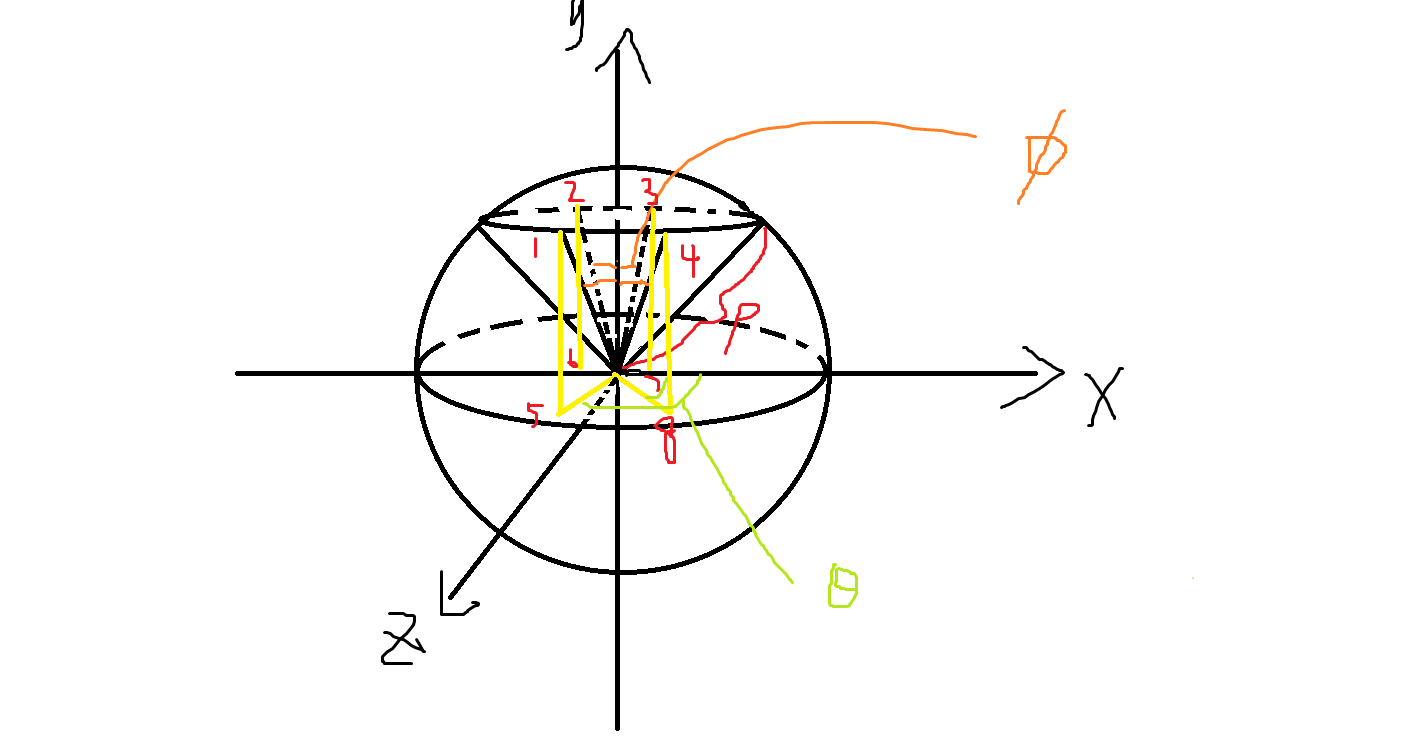
一图胜千言:
由ρ确定圆锥，由Ø确定1,2,3,4点（最终点就是其中一个），由θ确定5,6,7,8点然后对应上去找到1,2,3,4其中某点即为所要的点
转换公式
三角形：
i.直角也叫作底角
ii.1弧度 = 57.296°
注意点：计算sin cos tan慢，arc更加慢，应当确认是否确实需要知道角度值，若需要则可以用到查找表插值
iii.三角恒等变化
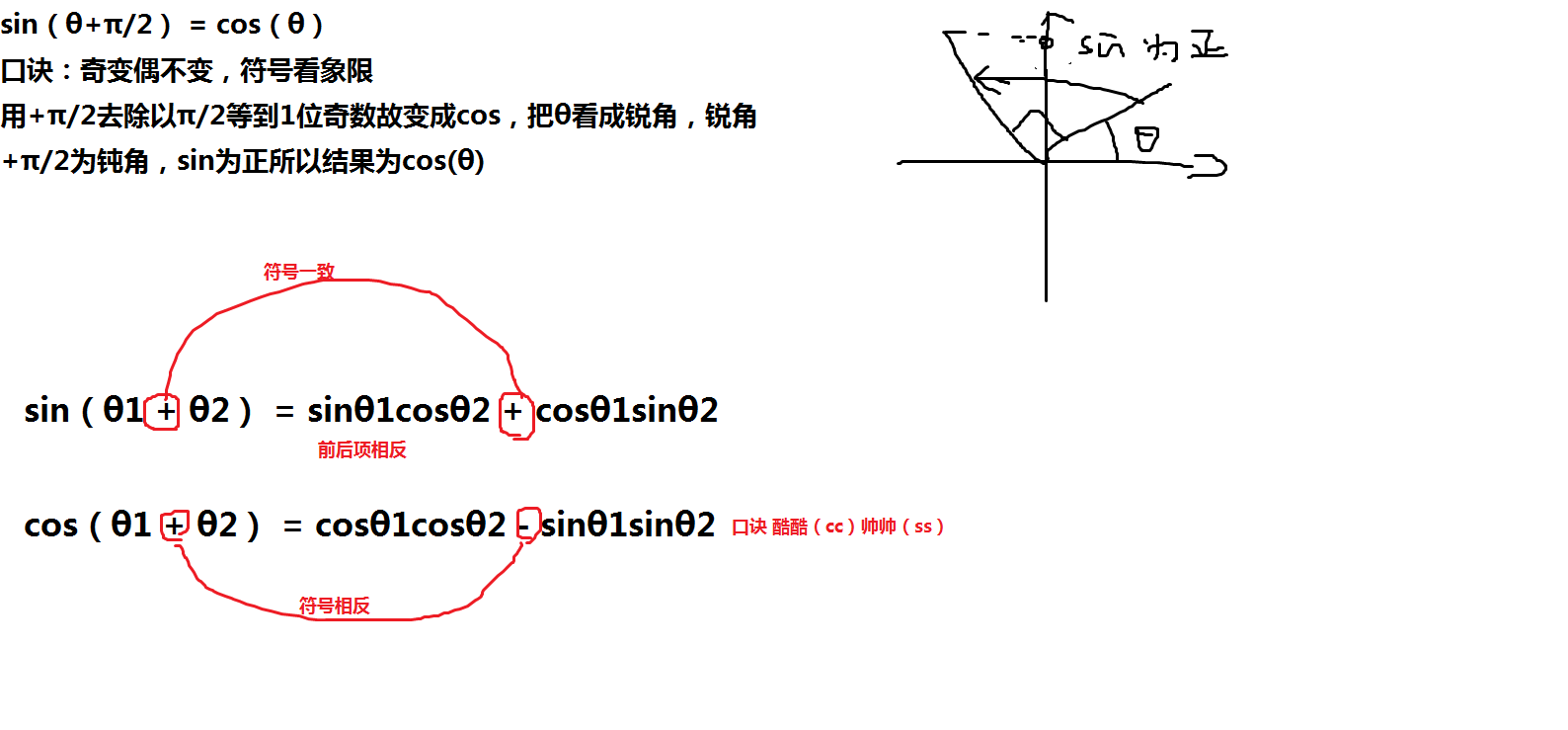
iV. //加粗为向量
I.有如下向量P1(x1,y1) P2(x2,y2)
U = P1 - P2 = (x2-x1,y2-y2) = <ux,uy> (ux，uy为分量)
（terminal point - initial point）
II.向量长度即为范数||U||表示
III.计算单位向量 n' = n / ||n||
IV.向量加法用平行四边形法则
V.向量减法
V.dot production
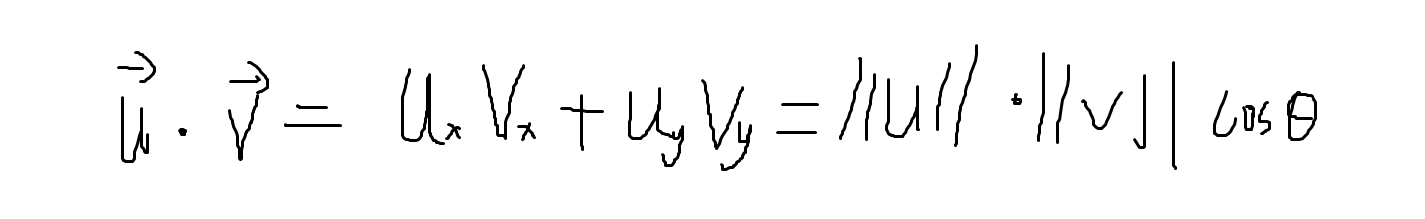
可以看出向量点乘是一个标量
应用：使用点乘可以计算出例如：物体A运动轨迹a，物体B运动轨迹b，求a在b上投影：
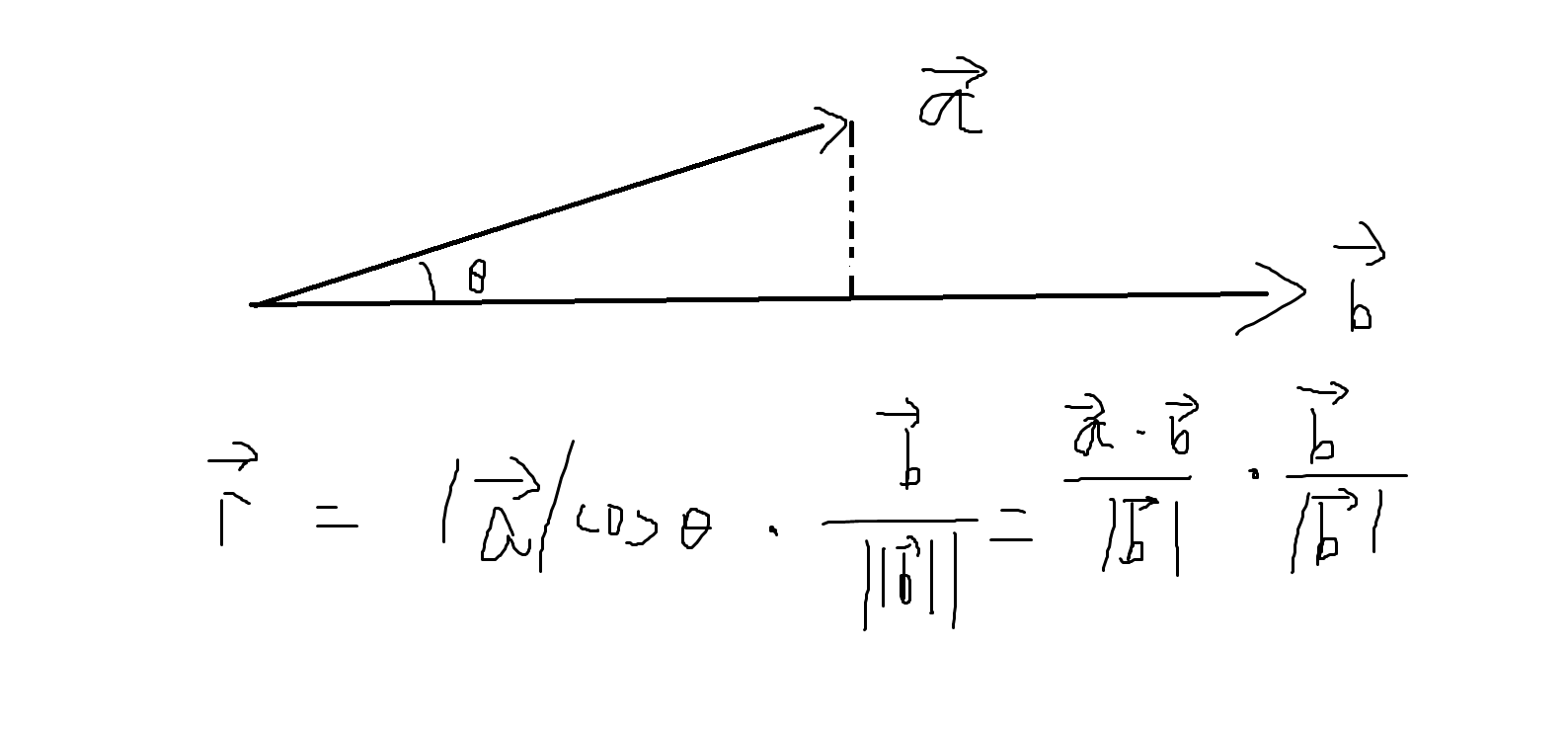（要求：一看到这种式子就应马上想到投影）
Vi.cross production
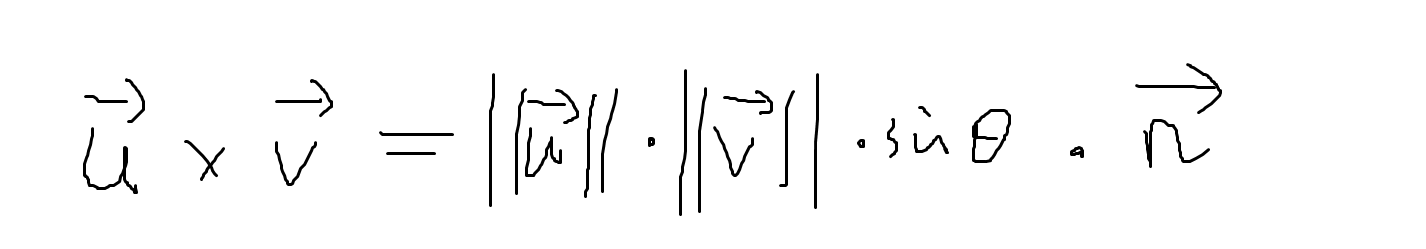（n为u和v构成平面的单位法向量，θ为uv两向量夹角）
计算n方法
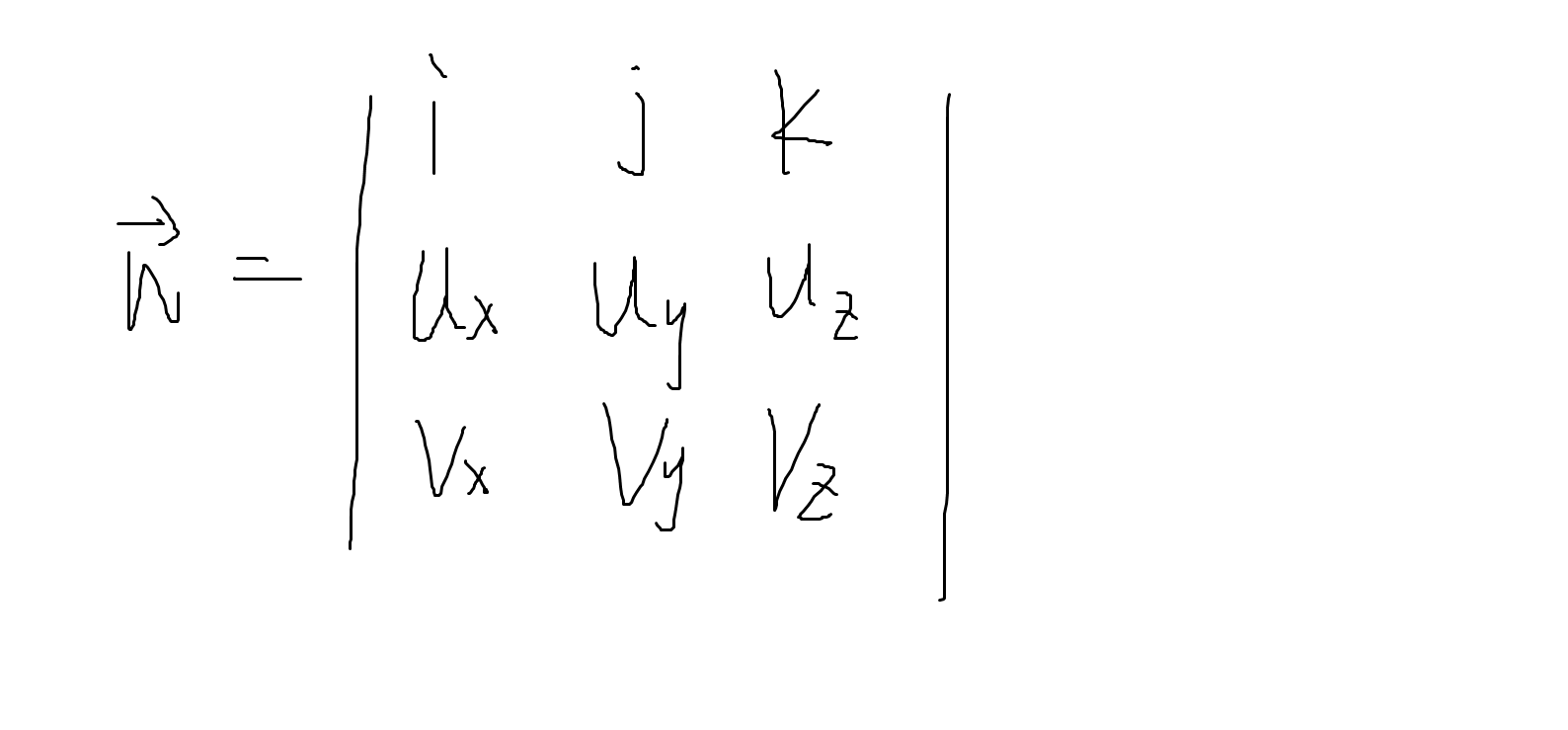等号右边为行列式，它的值即为n向量（i<1,0,0>，j<0,1,0>，k<0,0,1>为x，y，z轴上的单位向量）
今天内容就到这里，还有下集，欢迎指正和吐槽！XDDD