「JOISC 2020 Day3」收获

「JOISC 2020 Day3」收获

分类讨论.jpg

分析一棵苹果树被不断摘掉的过程，找到第一个摘它的人(i)

此后，每次摘它的人，就是(i)前面第一个距离它(ge C)的人，不妨设其为(nxt_i)

显然，(i,nxt_i)的关系，会构成基环内向树森林，每条内向边有一个权值(w_i)

容易(O(n))尺取得到(nxt_i,w_i)，考虑选择环上的一个点(u)，断开(u)对应的内向边，得到一棵树

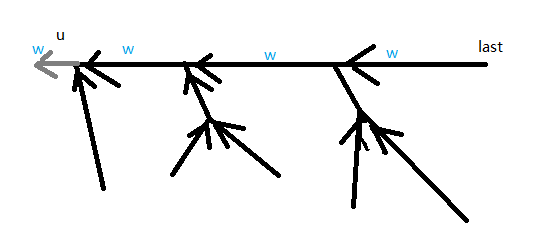
处理得到环长(len_u)，令(dis_u=w_u)，树上每个点的(dis_v=dis_{nxt_v}+w_v)

考虑一棵苹果树被第一次摘的情况，用一个二元组表示((v,t))，即被(v)在(t)时刻摘掉

我们认为是苹果树在基环内向树上走

1.苹果树不跨过(u)时的贡献

此时相当于每个((v,t))在往根节点走，贡献来自每个查询((x,d))的子树

即满足(vin subtree_x,dis_v-dis_x+tleq d)

离散之后可以用简单的 询问离线+(dfs)作差+树状数组解决

[ ]

2.跨过(u)，先将苹果树的贡献移动到(last)上，变为((last,t'=t+dis_v))

对于每个询问，显然必须满足(x)在环上

我们也可以令(d'=d-(len_u-dis_v))，同样将(x)移动到(last)上

此时只需要考虑每个(t')对于(d')的贡献

按照(len_u)，我们可以将(t',d')分段，每段都是([icdot len_u,(i+1)cdot len_u))的形式

2-1.对于不是同一段内的，每个(t')的对于(d')的贡献次数 就是 段编号 之差

2-2.同一段内，就是满足(t'leq d')且(t'mod len_uleq d'mod len_u) 的个数

将所有(d',t')排序后依次处理，容易通过参数分离处理2-1

对于2-2，将(t'mod len_u)离散后可以用树状数组处理

Loj Submission

空间复杂度为(O(n))，时间复杂度为(O(nlog n))

#include<bits/stdc++.h>
using namespace std;
using ll=int64_t;
#define pb push_back
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
ll rd(){
    char c;ll s=0;
    while(c=getchar(),c<48);
    do s=(s<<1)+(s<<3)+(c^'0');
    while(c=getchar(),c>47);
    return s;
}
enum{N=200010};
int n,m,q,nxt[N],L,C,C2,A[N*2],B[N],id[N],incir[N];
vector <int> E[N],G[N];
ll H[N],dis[N],H2[N],len[N],ans[N];
void dfs(int u){
    for(int i:E[u]) H[++C]=dis[u]+i;
    vector <int> tmp;
    for(int v:G[u]) {
        if(id[v]==id[u]) continue;
        tmp.pb(v),id[v]=id[u];
        dis[v]+=dis[u],dfs(v);
    }
    G[u]=tmp;
}

struct Node{ ll d; int id; };
vector <Node> Q[N],que;
vector <ll> upd;
struct BIT{
    int s[N],n;
    void Init(int m){ n=m,memset(s,0,(n+1)<<2); }
    void Add(int p,int x) { while(p<=n) s[p]+=x,p+=p&-p; }
    int Que(int p) {
        int res=0;
        while(p) res+=s[p],p-=p&-p;
        return res;
    }
} T,X;

// dfs作差处理情况1
void dfs2(int u){
    for(Node &i:Q[u]) {
        // 如果满足查询点在环上，就要加入2-1,2-2的计算
        if(incir[u]) {
            ll d=i.d-(len[id[u]]-dis[u]);
            if(d>=0) que.pb((Node){d,i.id});
        }
        // dfs作差-1
        ans[i.id]-=T.Que(i.d=upper_bound(H+1,H+C+1,dis[u]+i.d)-H-1);
    }
    for(int i:E[u]) T.Add(lower_bound(H+1,H+C+1,dis[u]+i)-H,1),upd.pb(dis[u]+i);
    for(int v:G[u]) dfs2(v);
    // dfs作差+1
    for(Node i:Q[u]) ans[i.id]+=T.Que(i.d);
}

int main(){
    n=rd(),m=rd(),L=rd(),C=rd();
    rep(i,0,n-1) A[i]=rd(),A[i+n]=A[i]+L;
    rep(i,0,m-1) B[i]=rd();
    int C_=C%L,p=0;
    // 尺取预处理i,nxt[i],w[i]
    rep(i,n,n*2-1) {
        while(p<i && A[i]-A[p+1]>=C_) p++;
        nxt[i-n]=p%n,G[p%n].pb(i-n);
        dis[i-n]=C-C_+A[i]-A[p];
    }
    p=0;
    // 预处理(v,t)
    rep(i,0,m-1) {
        while(p<n*2-1 && B[i]+L>=A[p+1]) p++;
        E[p%n].pb(B[i]+L-A[p]);
    }
    C=0;
    // 断环构建树
    rep(i,0,n-1) id[i]=-2;
    rep(i,0,n-1) if(id[i]==-2) {
        int u=i;
        for(;~id[u];u=nxt[u]) id[u]=-1;
        id[u]=u,len[u]=dis[u],incir[u]=1;
        for(int v=nxt[u];v!=u;v=nxt[v]) len[u]+=dis[v],incir[v]=1;
        dfs(u);
    }
    sort(H+1,H+C+1),T.Init(C=unique(H+1,H+C+1)-H-1);
    // 离线询问，权值离散
    rep(i,1,q=rd()) {
        int u=rd()-1; ll d=rd();
        Q[u].pb((Node){d,i});
    }
    rep(i,0,n-1) if(id[i]==i) {
        que.clear(),upd.clear();
        dfs2(i);
        sort(upd.begin(),upd.end()),sort(que.begin(),que.end(),[&](Node x,Node y){ return x.d<y.d; });
        C2=0;
        for(ll x:upd) H2[++C2]=x%len[i];
        sort(H2+1,H2+C2+1),X.Init(C2=unique(H2+1,H2+C2+1)-H2-1);
        auto it=upd.begin();
        ll s=0,c=0;
        for(Node &q:que) {
            while(it!=upd.end() && *it<=q.d) 
                X.Add(lower_bound(H2+1,H2+C2+1,*it%len[i])-H2,1),s+=*(it++)/len[i],c++;
            // 参数分离处理2-1
            ans[q.id]+=q.d/len[i]*c-s;
            // 树状数组查询2-2
            ans[q.id]+=X.Que(upper_bound(H2+1,H2+C2+1,q.d%len[i])-H2-1);
        }
    }
    rep(i,1,q) printf("%lld
",ans[i]);
}