COCI2013-2014 Contest#3 F 单调栈

COCI2013-2014 Contest#3 F 单调栈

考虑每个小区间([x_i,x_{i+1}])中，外部光照进来只能是这样

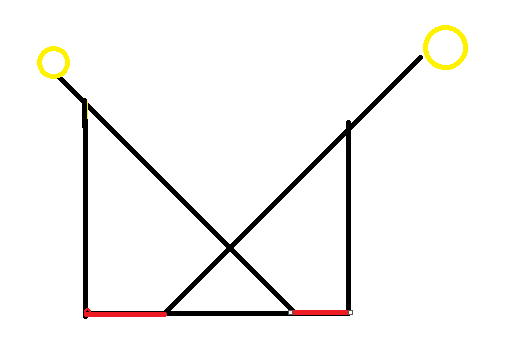
其中两边是光源，红色表示被照到了

那么所有合法的被照到的段可以表示为([x_i,x_{i+1}])中的两个小段，即

1.左边照进来的([s0_i,x_{i+1}])

2.右边照进来的([x_i,s1_i])

考虑从左到右维护可能照到右边的较优光源

显然对于每一个光源都有一个当前能遮住它最多的城市，构成(光源，限制城市)这样的点对

对于每一个较优的这样的点对 可以维护一个单调栈，维护出来应该是这样的

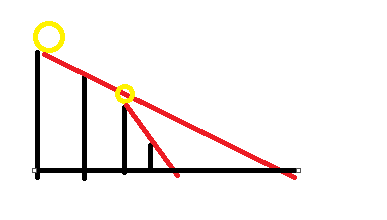
有几个较为显然的性质:

1.所有点对的(h_i)递减，否则要么是上一个光源被完全遮住了，要么是这个点可以遮住上一个光源更多

2.靠右的点对能够覆盖的范围较大，即可行区间的左端点较小

否则它此时不会产生贡献，而当后面较高的点进来时，相对更矮的它也更容易被遮住

实际上，这样的形状就会构成一个类似上凸包的东西，但是凸包上只有一部分点产生贡献

[ ]

考虑依次加入点((x_i,h_i))，显然可以弹掉(h_j<h_i)的所有点对(为了防止下面计算左端点时出现问题)

接下来的情况，类似维护凸包，但是要考虑更新限制城市 或者 弹掉点对

[ ]

对于向左的情况，反着求一遍即可，最后可以减去两种区间都覆盖不到的部分

#include<bits/stdc++.h>
using namespace std;
typedef double db;
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)

char IO;
template <class T=int> T rd(){
	T s=0; int f=0;
	while(!isdigit(IO=getchar())) if(IO=='-') f=1;
	do s=(s<<1)+(s<<3)+(IO^'0');
	while(isdigit(IO=getchar()));
	return f?-s:s;
}

const int N=3e5+10;

int n,D;
struct City{ int k,x,h; } C[N];

struct Lightpair{
	//描述一个灯塔和右边遮住它最多的城市
	int x,y;
	Lightpair(const int &_x=0,const int &_y=0) : x(_x),y(_y) { }
	db Left(){
		return C[y].x+1.0*(C[y].x-C[x].x)/(C[x].h-C[y].h)*C[y].h;
	}
	// z这个发光对能照到的范围为[Left(),+oo)
} stk[N];
int top;
void Cover(Lightpair &x,int y){ if(Lightpair(x.x,y).Left()>x.Left()) x.y=y; }
db s[2][N];
// 将所有可能的发光区间描述为 [C[i].x,s[k][i]]


int main(){
	n=rd(),D=rd();
	rep(i,1,n) C[i].k=rd(),C[i].x=rd(),C[i].h=rd();
	C[n+1].x=D;
	rep(k,0,1) {
		rep(i,0,n) {
			while(top && C[stk[top].x].h<=C[i].h) top--; // 完全被遮住的，先弹掉
			if(top) {
				Cover(stk[top],i);
				while(top>1){
					Cover(stk[top-1],i);
					if(stk[top-1].Left()>stk[top].Left()) break;
					top--;
				}
			}
			if(C[i].k) stk[++top]=i,s[k][i]=C[i].x; // 一定覆盖C[i].x,C[i+1].x
			else if(top) s[k][i]=min(stk[top].Left(),(db)C[i+1].x); // 尝试让当前最优的点对覆盖过来
			else s[k][i]=C[i+1].x; // 无覆盖
		}
		if(!k) {
			reverse(C+1,C+n+1),top=0;
			rep(i,1,n) C[i].x=D-C[i].x;
		} else {
			reverse(s[k],s[k]+n+1);
			rep(i,0,n) s[k][i]=D-s[k][i];
		}
	}
	db ans=D; // 减去不合法的
	rep(i,0,n) if(s[0][i]>s[1][i]) ans-=s[0][i]-s[1][i];
	printf("%.3lf
",ans);
}