树形dp专题总结

树形dp专题总结

大力dp的练习与晋升

原题均可以在网址上找到

技巧总结

1.换根大法

2.状态定义应只考虑考虑影响的关系

3.数据结构与dp的合理结合(T11)

4.抽直径解决求最长链的许多类问题(T12)

5.dp题最基本的考察是对题意模型的转化，以应用在各个方面

6.前缀和等技巧优化dp

7.树形背包是n*n的！

T1 BZOJ1304 [CQOI2009]叶子的染色

首先是对于固定根节点的\(dp\)

\(dp\)状态\(dp[3]\)为子树还需要颜色\(1,2\)，或不需要

转移比较简单，关键在于根节点不固定

int dp[N][4],t[N];//0无,1,2
void dfs(int u,int f){
    if(u<=m) return;
    dp[u][0]=dp[u][1]=dp[u][2]=0;
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        dfs(v,u);
        dp[u][0]+=min(dp[v][0],dp[v][2]);
        dp[u][1]+=min(dp[v][1],dp[v][2]);
        dp[u][2]+=dp[v][2];
    }
    dp[u][2]=min(dp[u][2],min(dp[u][0],dp[u][1])+1);
}

这一点，我们可以两遍\(dfs\)换根,但是网上的神仙们都有证明不同根节点都不会影响答案,->传送门

事实上，在bzoj上直接\(n^2\)也能过。。。

\[\ \]

T2 BZOJ 4726 POI2017 Sabota

关键点捕捉->叛徒一定在叶子上，最后一定是一整颗子树变成叛徒，所以dp每一颗子树成为叛徒的最值即可

(放心不会炸精度)

double k,ans=0;
 
double dp[N];
int sz[N];
void dfs(int u,int f){
    sz[u]=1;
    dp[u]=0;
    int son=0;
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        dfs(v,u);
        sz[u]+=sz[v];
        son++;
    }
    if(!son) dp[u]=1;
    else {
        erep(u,i) {
            int v=e[i].to;
            if(v==f) continue;
            dp[u]=max(dp[u],min(dp[v],1.0*sz[v]/(sz[u]-1)));
            son++;
        }
    }
    //cout<<u<<' '<<dp[u]<<endl;
    if(sz[u]>m) ans=max(ans,dp[u]);
}
 
 
int main() {
    n=rd(),m=rd();
    rep(i,2,n) {
        int u=i,v=rd();
        AddEdge(u,v);
        AddEdge(v,u);
    }
    dfs(1,0);
    printf("%.7lf\n",ans);
}

T3 BZOJ3743 [Coci2015]Kamp

其实这是一道很标准的换根求距离

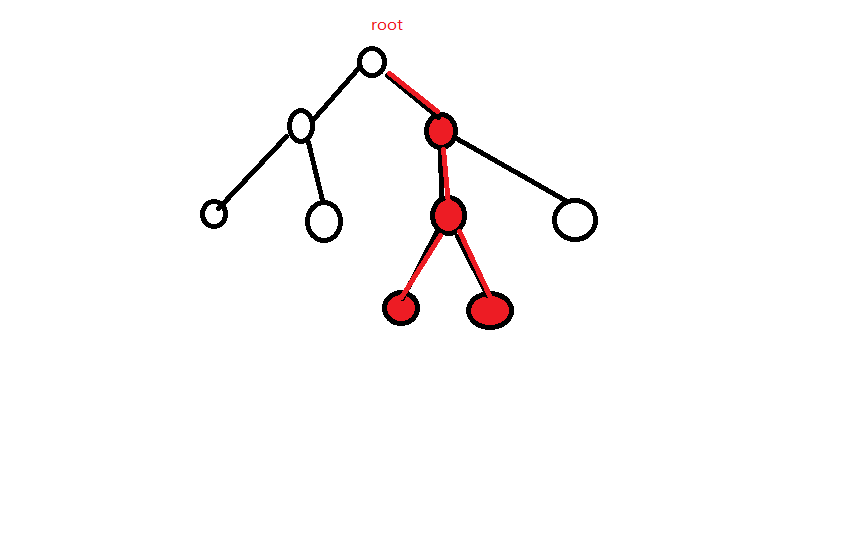
在这张图中，计算根到所有红色节点的方案

先假设最后还回到根，则会遍历每一条红色的边两次，而事实上最后我们可以停在一个节点上

所以取一个最远的红点停下来就好了

 
ll dp[N],ma[N][4],g[N];
//dp -> 所有红色边的和
//ma -> 最远的红点
void dfs1(int u,int f){
    sz[u]=mk[u];
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        dfs1(v,u);
        if(sz[v]) {
            dp[u]+=dp[v]+e[i].w*2;
            ma[u][3]=ma[v][0]+e[i].w;
            sort(ma[u],ma[u]+4,greater<ll>());
        }
        sz[u]+=sz[v];
    }
}
 
void dfs2(int u,int f,int ew,ll w){
    g[u]=dp[u];
    if(f) {
        if(sz[u]<m) {
            g[u]+=g[f]+ew*2;
            if(sz[u]) g[u]-=dp[u]+2*ew;
        }
    }
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        ll t=w;
        if(sz[v]&&ma[u][0]==ma[v][0]+e[i].w)t=max(t,ma[u][1]);
        else t=max(t,ma[u][0]);
        dfs2(v,u,e[i].w,t+e[i].w);
    }
    ma[u][3]=w;
    sort(ma[u],ma[u]+4,greater<ll>());
}
 
 
 
 

\[\ \]

\[\ \]

T4 [BZOJ4007] [JLOI2015]战争调度

这题的复杂度非常暴力

\(dp[i][j][k]\)表示当前到第i个叶子节点，共选了j个点，它的祖先就业情况为k

对于\(i\)与\(i+1\)的叶子结点，他们有一段公共的祖先必须相同，其它的可以任意取，所以可以枚举相同的，再枚举不同的，将复杂度降到\(2^{(3n-3)}\)

int dp[2][N][N];
int a[2][N<<1][10],s[2][N<<1][N];
int Log[N<<1];
 
int main() {
    rep(i,2,(1<<10)) Log[i]=Log[i>>1]+1;
    n=rd(),t=n-1,m=rd();
    rep(i,(1<<t),(1<<n)-1) rep(j,0,t-1) a[1][i][j]=rd();
    int cur=0,A=(1<<t)-1;
    rep(i,(1<<t),(1<<n)-1) {
        rep(j,0,t-1) a[0][i][j]=rd();
        rep(j,0,A) {
            rep(k,0,t-1) if(j&(1<<k)) s[1][i][j]+=a[1][i][k];
            else s[0][i][j]+=a[0][i][k];
        }
    }
    rep(i,(1<<t),(1<<n)-1) {
        cur^=1;
        if(i==(1<<t)) {
            rep(j,0,A) {
                dp[cur][j][0]=s[0][i][j];
                dp[cur][j][1]=s[1][i][j];
            }
        } else {
            int my=Log[i&-i],his=t-my;//lowbit即LCA
            rep(d,0,m) {
                rep(j,0,(1<<his)-1) {//枚举公共部分
                    int ma1=0,ma2=0;
                    rep(k,0,(1<<my)-1) {//枚举上一位选了什么
                        chk(ma1,dp[!cur][(j<<my)|k][d]);
                        if(d) chk(ma2,dp[!cur][(j<<my)|k][d-1]);
                    }
                    rep(k,0,(1<<my)-1) {//转移这一位选了什么
                        dp[cur][(j<<my)|k][d]=ma1+s[0][i][(j<<my)|k];
                        if(d) {
                            chk(dp[cur][(j<<my)|k][d],ma2+s[1][i][(j<<my)|k]);
                        }
                    }
                }
            }
        }
    }
    int ans=0;
    rep(i,0,A) rep(j,0,m) chk(ans,dp[cur][i][j]);
    printf("%d\n",ans);
}

\[\ \]

\[\ \]

T5 4238电压

其实是一个二分图染色问题，并不是树形dp

一个二分图成立的条件即不存在奇环

但是在这题的限制条件下，断开偶环同样不成立，因为根本断不开。。。电流依然存在

所以就是求所有的边能覆盖所有的奇环，并且不被任意一个偶环覆盖

这个东西其实树上差分就能搞定，是我写麻烦了

int n,t,m;
 
struct Edge{
    int to,nxt,id;
}e[N<<1];
int head[N],ecnt;
void AddEdge(int u,int v,int id) {
    e[++ecnt]=(Edge){v,head[u],id};
    head[u]=ecnt;
}
#define erep(u,i) for(int i=head[u];i;i=e[i].nxt)
 
int eu[N],ev[N];
int vis[N],intree[N],fa[N];
int sz[N],son[N],top[N],dep[N];
 
int ans,cnt;
 
void dfs1(int u,int f){
    vis[u]=1;
    sz[u]=1,fa[u]=f;
    erep(u,i) {
        int v=e[i].to;
        if(vis[v]) continue;
        intree[e[i].id]=1;
        dep[v]=dep[u]+1;
        dfs1(v,u);
        sz[u]+=sz[v];
        if(sz[son[u]]<sz[v]) son[u]=v;
    }
}
 
int L[N],R[N],dfn,id[N];
int s[N];
 
void dfs2(int u,int t){
    id[L[u]=++dfn]=u;
    top[u]=t;
    if(son[u]) dfs2(son[u],t);
    erep(u,i) {
        int v=e[i].to;
        if(v==son[u]||v==fa[u]||!intree[e[i].id]) continue;
        dfs2(v,v);
    }
    R[u]=dfn;
}
 
int sum[N];
int LCA(int x,int y){
    while(top[x]!=top[y]) {
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        x=fa[top[x]];
    }
    if(dep[x]<dep[y]) swap(x,y);
    return y;
}
 
 
void Up(int x,int y){
    int lca=LCA(x,y),len=dep[x]+dep[y]-dep[lca]*2+1;
    if(len&1) {
        ans=len;
        cnt++;
        while(top[x]!=top[y]) {
            if(dep[top[x]]<dep[top[y]]) swap(x,y);
            sum[L[top[x]]]++,sum[L[x]+1]--;
            x=fa[top[x]];
        }
        if(dep[x]<dep[y]) swap(x,y);
        if(x!=y) sum[L[y]+1]++,sum[L[x]+1]--;
        return;
    }
    while(top[x]!=top[y]) {
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        s[L[top[x]]]++,s[L[x]+1]--;
        x=fa[top[x]];
    }
    if(dep[x]<dep[y]) swap(x,y);
    if(x!=y) s[L[y]+1]++,s[L[x]+1]--;
}
 
 
int rt[N],c;
 
 
int main() {
    n=rd(),m=rd();
    rep(i,1,m) {
        eu[i]=rd(),ev[i]=rd();
        AddEdge(eu[i],ev[i],i);
        AddEdge(ev[i],eu[i],i);
    }
    rep(i,1,n) if(!vis[i]) dfs1(rt[++c]=i,0);
    rep(i,1,c) dfs2(rt[i],1);
    rep(i,1,m) if(!intree[i]) Up(eu[i],ev[i]);
    rep(i,1,n) s[i]+=s[i-1];
    rep(i,1,c) s[L[rt[i]]]=1;
    if(cnt) {
        rep(i,1,n) sum[i]+=sum[i-1];
        ans=0;
        rep(i,1,n) if(sum[i]==cnt&&!s[i]) ans++;
        if(cnt==1) ans++; //cnt=1时，可以断树外的那条边
        return printf("%d\n",ans),0;
    }
    rep(i,1,n) if(!s[i]) ans++;
    printf("%d\n",ans);
}
 

\[\ \]

\[\ \]

T6 [BZOJ1509] [NOI2003]逃学的小孩]

题意可能会有点绕，好好理解一下

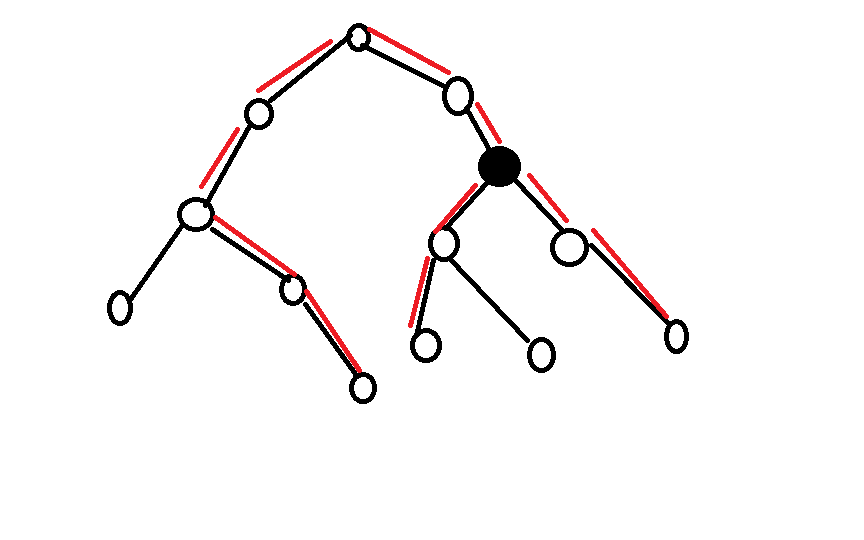
在这张图中，我们枚举黑点为三个点路径的交点

则最优的三个点一定是途中红色路径所到达的三个点

即树内两条最长链，树外一条最长链

接下来你可以直接枚举\(A,B,C\)的位置，但是其实可以发现，三条链中最多只有一条会被遍历两次，而两次不会出现在最长边上，所以我们让次长边被遍历两边即可

struct Node{
    ll a[4];
    void operator += (const int x) {
        a[3]=x;
        sort(a,a+4,greater<ll>());
    }
}g[N];
 
ll ans;
 
void dfs1(int u,int f){ 
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        dfs1(v,u);
        g[u]+=g[v].a[0]+e[i].w;
    }
}
 
 
 
 
void dfs2(int u,int f,ll w) {
    ll t[5];
    rep(i,0,2) t[i]=g[u].a[i];
    t[3]=w;
    sort(t,t+4,greater<ll>());
    ans=max(ans,t[0]+t[1]*2+t[2]);
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        ll t=w;
        if(g[u].a[0]==g[v].a[0]+e[i].w) t=max(t,g[u].a[1]);
        else t=max(t,g[u].a[0]);
        dfs2(v,u,t+e[i].w);
    }
}

\[\ \]

\[\ \]

T7 3696. 化合物

没办法，正解FWT不会，只能写暴力水

int maxdep[N];
void dfs(int u,int f){
    maxdep[u]=0;
    dp[u][0]++;
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        dfs(v,u);
        for(reg int j=0;j<=maxdep[u];++j) for(reg int k=0;k<=maxdep[v];++k) cnt[j^(k+1)]+=1ll*dp[u][j]*dp[v][k];
        rep(j,0,maxdep[v]) dp[u][j+1]+=dp[v][j];
        maxdep[u]=max(maxdep[u],maxdep[v]+1);
    }
}
 

\[\ \]

\[\ \]

T8 BZOJ4824 [Cqoi2017]老C的键盘

这题主要是要想到dp状态，转移其实并不难，并且这道题和 T10 [[BZOJ3167][Heoi2013]Sao] 一样

dp状态:

\(dp[i][j]\)表示第\(i\)棵子树, \(i\)号节点在子树中排名为\(j\)的方案数, 因为只用考虑相邻节点大小的关系，所以可以比较简单的转移

若确定在已经合并的总子树中，当前节点为\(u\)，将要被合并上来的节点为\(v\) , \(v\) 的子树中贡献了\(j\)个权值小于\(u\)的点，并且\(v\)小于\(u\)

则有\(dp[u][i+j]=dp[u][i]*dp[v][1..j]*C(i-1+j,j)*C(sz[u]-i+sz[v]-j,sz[v]-j)\)

即确定\(i\)，\(j\)关系，将小于\(u\)的和大于\(u\)的合并点可以分别任意排列大小,是一个简单的树形背包

关于这个组合数，我的代码里写的不一样，其实也可以这样理解

设\(k\)个子树里传进\(c[1..k]\)个小于\(u\)的数

那么我们先假设将这些所有的数排列，总共的方案即\((\sum_{i=1}^{i \leq k} \ c[i])!\)

然而子树里的排布顺序其实已经固定，所以还要分别除掉Meiz每一棵子树里的排布方案，即\(\Pi_{i=1}^{i \leq k} \ c[i]!\)

发现对于转移最后得到的所有\(dp[u][i]\),总方案为\(i!\)，所以只要在转移时乘上逆元即可

由于要访问\(dp[v][1..j]\)，所以还要前缀和一下

大于号就是反过来

ll po[N]={1,1},Inv[N]={1,1};
ll dp[N][N],tmp[N];
int sz[N];
void dfs(int u,int f){
    memset(dp[u],0,sizeof dp[u]);
    sz[u]=dp[u][1]=1;
    erep(u,t) {
        int v=e[t].to,w=e[t].w;
        if(v==f) continue;
        dfs(v,u);
        memset(tmp,0,sizeof tmp);
        if(w) {
            rep(i,1,sz[v]) (dp[v][i]+=dp[v][i-1])%=P;
            rep(i,1,sz[u]) {
                rep(j,1,sz[v]) {
                    (tmp[i+j]+=Inv[j]*Inv[sz[v]-j]%P*dp[u][i]%P*dp[v][j]%P)%=P;
                }
            }
        } else {
            drep(i,sz[v],1) (dp[v][i]+=dp[v][i+1])%=P;
            rep(i,1,sz[u]) {
                rep(j,1,sz[v]) {
                    (tmp[i+j-1]+=Inv[j-1]*Inv[sz[v]-j+1]%P*dp[u][i]%P*dp[v][j]%P)%=P;
                }
            }
        }
        sz[u]+=sz[v];
        rep(i,1,sz[u]) dp[u][i]=tmp[i];
    }
    rep(i,1,sz[u]) dp[u][i]=dp[u][i]*po[i-1]%P*po[sz[u]-i]%P;
}
 
 
 
 
 
 
void _main(){
    n=rd();
    rep(i,1,n) head[i]=0;ecnt=0;
    rep(i,2,n) {
        int u=rd()+1,t=getchar(),v=rd()+1;
        if(t=='<') t=0;
        else t=1;
        AddEdge(u,v,t);
        AddEdge(v,u,!t);
    }
    dfs(1,0);
    ll ans=0;
    rep(i,1,n) ans+=dp[1][i];
    ans%=P;
    printf("%lld\n",ans);
}
 
int main(){
    rep(i,2,N-1) {
        po[i]=po[i-1]*i%P;
        Inv[i]=(P-P/i)*Inv[P%i]%P;
    }
    rep(i,1,N-1) Inv[i]=Inv[i-1]*Inv[i]%P;
    rep(kase,1,rd()) _main();
}
 
 

\[\ \]

\[\ \]

T9 [BZOJ1808][IOI2007]training 训练路径]

整个题的模型其实比较好想，关键是最后这个dp转移的实现

题意即给出了树边和非树边，要求去掉一些非树边使得图上没有偶环

对于偶环：当然全部去掉啊！

对于奇环：若两个奇环在树上的覆盖区域(是一个树边的连续路径)有重叠，则它们可以构成偶环,依然要去掉一部分

难点在于重叠部分dp难以转移 (好像可以二分图最大权值匹配)

肯定是要把环挂在\(LCA\)上处理

定义状态\(dp[u]\)为选择整个环在\(u\)的子树里的环最大能保留的权值

环的点可以重叠，但边不行，所以每一个点的每一个儿子都最多只会被一个奇环覆盖

而一个奇环最多覆盖两个节点，所以定义辅助\(tmp[u][S]\)表示\(u\)的子树里儿子被覆盖的状态为\(S\)

这里关于覆盖我的写法里还有一种覆盖-->:直接把儿子的\(dp[son]\)转移过来

当你在\(u\)处转移到一个环两个端点为\(x,y\)时，它的贡献不止是环的权值，还有两个儿子里没有被影响到的\(dp\)值总和

这个东西我们用一个数组\(g[u][v]\)存下来，每次都遍历一遍预处理出来

如何预处理？每遍历一个儿子就累和\(tmp[u][S - (1<<sonid)]\),就去掉了被影响部分的答案

还有就是\(tmp[u][S]\)要进行子集累最大值

int n,m;
 
struct Edge{
    int to,nxt;
}e[N<<1];
int head[N],ecnt;
void AddEdge(int u,int v) {
    e[++ecnt]=(Edge){v,head[u]};
    head[u]=ecnt;
}
#define erep(u,i) for(int i=head[u];i;i=e[i].nxt)
 
int fa[N][14],dep[N];
void pre_dfs(int u,int f){
    fa[u][0]=f;
    for(int i=1;(1<<i)<=dep[u];++i) fa[u][i]=fa[fa[u][i-1]][i-1]; 
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        dep[v]=dep[u]+1;
        pre_dfs(v,u);
    }
}
 
 
 
 
int Up(int x,int k) {
    for(int i=0;(1<<i)<=k;++i) if(k&(1<<i)) x=fa[x][i];
    return x;
}
int LCA(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    x=Up(x,dep[x]-dep[y]);
    if(x==y) return x;
    drep(i,10,0) if(dep[x]>=(1<<i) && fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}
 
 
 
struct node{
    int x,y;
};
struct Node{
    int c,w;
    node a[2];
};
int eu[M],ev[M],ew[M],mm;
vector <Node> G[N];
 
 
 
int dp[N],g[N][N];
int c[M],val[M];
int id[N][N];
 
int tmp[N][1<<10],son[N];
void dfs_getg(int rt,int u,int f,int w){
    g[rt][u]=w;
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        dfs_getg(rt,v,u,w+tmp[u][((1<<son[u])-1)^(1<<id[u][v])]);
    }
}//处理g数组
 
 
 
 
void dfs_getdp(int u,int f){
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        dfs_getdp(v,u);
        dfs_getg(u,v,u,0);
    }
    int n=0;
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        id[u][v]=n++;
        son[u]++;
    }
    int m=G[u].size();
    rep(i,0,m-1) {
        c[i]=0;
        val[i]=G[u][i].w;
        rep(j,0,G[u][i].c-1) val[i]+=g[u][G[u][i].a[j].x]+dp[G[u][i].a[j].x],c[i]|=1<<id[u][G[u][i].a[j].y];
    }//处理链的贡献
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        c[m]=1<<id[u][v];
        val[m++]=dp[v];
    }//儿子直接转移上来
    rep(S,0,(1<<n)-1) {
        rep(i,0,m-1) {
            if(S&c[i]) continue;
            tmp[u][S|c[i]]=max(tmp[u][S|c[i]],tmp[u][S]+val[i]);
        }
        rep(j,0,n-1) if(S&(1<<j)) tmp[u][S]=max(tmp[u][S],tmp[u][S^(1<<j)]);//子集累最大值
        dp[u]=max(dp[u],tmp[u][S]);
    }//处理tmp数组
}
 
 
int main(){ 
    n=rd(),m=rd();
    rep(i,1,m) {
        int u=rd(),v=rd(),w=rd();
        if(!w) {
            AddEdge(u,v);
            AddEdge(v,u);//树边
        } else {
            eu[++mm]=u;
            ev[mm]=v;
            ew[mm]=w;//存环
        }
    }
    m=mm;
    pre_dfs(1,0);
    int sum=0;
    rep(i,1,m) {
        int x=eu[i],y=ev[i];
        sum+=ew[i];
        if(dep[x]<dep[y]) swap(x,y);
        int lca=LCA(x,y);
        if((dep[x]+dep[y]-2*dep[lca])&1) continue;//偶环
        Node t;t.c=0,t.w=ew[i];
        t.a[t.c++]=(node){x,Up(x,dep[x]-dep[lca]-1)};
        if(y!=lca) t.a[t.c++]=(node){y,Up(y,dep[y]-dep[lca]-1)};
        G[lca].push_back(t);
    }
    dfs_getdp(1,0);
    printf("%d\n",sum-dp[1]);
}
 
 
 

\[\ \]

\[\ \]

T10 同 T8

\[\ \]

\[\ \]

T11 2164. 采矿

这题难度在于读题和对算法暴力程度的评估...

因为每个点没有互相影响，所以直接线段树存储子树信息，\(m^2\)合并区间的\(dp\)值

对于到根的路径上的点，取每个点权值max即可，树剖线段树

总复杂度\(O(C \cdot N \cdot log \ n \cdot m^2+C \cdot log^2 n \cdot m)\)

int n,m,A,B,Q;
int fa[N];
vector <int> G[N];
template <typename T> void chk(T &a,T b) { ((a<b)&&(a=b)); }
 
int L[N],R[N],id[N],dfn,sz[N],son[N],top[N],dep[N];
void dfs1(int u) {
    sz[u]=1;
    rep(i,0,G[u].size()-1) {
        int v=G[u][i];
        dep[v]=dep[u]+1;
        dfs1(v);
        sz[u]+=sz[v];
        if(sz[v]>sz[son[u]]) son[u]=v;
    }
}
void dfs2(int u,int t){
    id[L[u]=++dfn]=u;
    top[u]=t;
    if(son[u]) dfs2(son[u],t);
    rep(i,0,G[u].size()-1) {
        int v=G[u][i];
        if(v==son[u]) continue;
        dfs2(v,v);
    }
    R[u]=dfn;
}
 
inline int Get() {
    A=(0ll+(A^B)+(B/X)+1ll*B*X)&Y;
    B=(0ll+(A^B)+(A/X)+1ll*A*X)&Y;
    return (A^B)%Q;
}
 
struct Node{
    ll a[51];
    void Getline() {
        rep(i,1,m) a[i]=Get();
        sort(a+1,a+m+1);
    }
    Node operator + (const Node x) const{
        Node res; memset(res.a,0,sizeof res.a);
        rep(i,0,m) rep(j,0,m-i) chk(res.a[i+j],a[i]+x.a[j]);
        return res;
    }
}C[N],dp[N<<2];
 
void Build(int p,int l,int r){
    if(l==r) {
        dp[p]=C[id[l]];
        return;
    }
    int mid=(l+r)>>1;
    Build(p<<1,l,mid);
    Build(p<<1|1,mid+1,r);
    dp[p]=dp[p<<1]+dp[p<<1|1];
}
void Upd(int p,int l,int r,int x){
    if(l==r) {
        dp[p]=C[id[l]];
        return;
    }
    int mid=(l+r)>>1;
    if(x<=mid) Upd(p<<1,l,mid,x);
    else Upd(p<<1|1,mid+1,r,x);
    dp[p]=dp[p<<1]+dp[p<<1|1];
}
Node Que(int p,int l,int r,int ql,int qr) {
    if(l==ql&&qr==r) return dp[p];
    int mid=(l+r)>>1;
    if(qr<=mid) return Que(p<<1,l,mid,ql,qr);
    else if(ql>mid) return Que(p<<1|1,mid+1,r,ql,qr);
    else return Que(p<<1,l,mid,ql,mid)+Que(p<<1|1,mid+1,r,mid+1,qr);
}
 
struct SGT{
    int s[N<<2];
    void Build(int k,int p,int l,int r) {
        if(l==r) {
            s[p]=C[id[l]].a[k];
            return;
        }
        int mid=(l+r)>>1;
        Build(k,p<<1,l,mid);
        Build(k,p<<1|1,mid+1,r);
        s[p]=max(s[p<<1],s[p<<1|1]);
    }
    void Upd(int p,int l,int r,int x,int y){
        if(l==r) {
            s[p]=y;
            return;
        }
        int mid=(l+r)>>1;
        if(x<=mid) Upd(p<<1,l,mid,x,y);
        else Upd(p<<1|1,mid+1,r,x,y);
        s[p]=max(s[p<<1],s[p<<1|1]);
    }
    int Que(int p,int l,int r,int ql,int qr) {
        if(l==ql&&r==qr) return s[p];
        int mid=(l+r)>>1;
        if(qr<=mid) return Que(p<<1,l,mid,ql,qr);
        else if(ql>mid) return Que(p<<1|1,mid+1,r,ql,qr);
        else return max(Que(p<<1,l,mid,ql,mid),Que(p<<1|1,mid+1,r,mid+1,qr));
    }
}tr[51];
 
 
 
 
 
 
int main() { 
    n=rd(),m=rd(),A=rd(),B=rd(),Q=rd();
    rep(i,2,n) G[fa[i]=rd()].push_back((int)i);
    dep[1]=1;dfs1(1),dfs2(1,1);
    rep(i,1,n) C[i].Getline();
    Build(1,1,n);
    rep(i,1,m) tr[i].Build(i,1,1,n);
    rep(i,1,rd()) {
        int opt=rd();
        if(opt==0) {
            int p=rd();
            C[p].Getline();
            Upd(1,1,n,L[p]);
            rep(i,1,m) tr[i].Upd(1,1,n,L[p],C[p].a[i]);
        } else {
            int x=rd(),y=rd();
            Node res=Que(1,1,n,L[x],R[x]);
            ll ans=res.a[m];
            int t=fa[x];
            if(t&&x!=y) {
                while(top[t]!=top[y]) {
                    rep(j,0,m-1) chk(ans,res.a[j]+tr[m-j].Que(1,1,n,L[top[t]],L[t]));
                    t=fa[top[t]];
                }
                rep(j,0,m-1) chk(ans,res.a[j]+tr[m-j].Que(1,1,n,L[y],L[t]));
            }
            printf("%lld\n",ans);
        }
    }
}

\[\ \]

\[\ \]

T12 [BZOJ4890] [TJOI2017]城市

\(n^2\)大暴力可水

枚举断开的边，两边要使最小，应是取出两边的直径中点相连，否则两条直径相接的路径会很长

所以就可以暴力了呀

int eu[N],ev[N],ew[N];
int vis[N],fa[N],fe[N],fid[N];
int ma,id;
void dfs(int u,int f,int d){
    if(d>ma) ma=d,id=u;
    erep(u,i) {
        int v=e[i].to;
        if(v==f||vis[v]) continue;
        fa[v]=u,fe[v]=e[i].w,fid[v]=(i+1)/2+1;
        dfs(v,u,d+e[i].w); 
    }
}
int can[N];
 
 
 
int main(){ 
    n=rd();
    rep(i,2,n) {
        int u=rd(),v=rd(),w=rd();
        AddEdge(u,v,w);
        AddEdge(v,u,w);
        eu[i]=u,ev[i]=v,ew[i]=w;
    }
    ma=-1;
    dfs(1,0,0);
    int rt=id;
    ma=-1;
    dfs(rt,0,0);
    while(id!=rt) {
        can[fid[id]]=1;
        id=fa[id];
    }
    int ans=ma;
    rep(i,2,n) if(can[i]) {
        vis[eu[i]]=1;
        ma=-1;
        dfs(ev[i],0,0);
        int rt=id;
        ma=-1;
        dfs(rt,0,0);
        vis[eu[i]]=0;
        int l=ma,mid,rmid;
        while(1) {
            if(l>=ma/2) mid=l;
            if(l<=ma/2) {
                rmid=l;
                break;
            }
            l-=fe[id];
            id=fa[id];
        }
        int t=min(max(mid,ma-mid),max(rmid,ma-rmid)),t1=ma;
 
        vis[ev[i]]=1;
        ma=-1;
        dfs(eu[i],0,0);
        rt=id;
        ma=-1;
        dfs(rt,0,0);
        vis[ev[i]]=0;
        l=ma;
        while(1) {
            if(l>=ma/2) mid=l;
            if(l<=ma/2) {
                rmid=l;
                break;
            }
            l-=fe[id];
            id=fa[id];
        }
        int t2=min(max(mid,ma-mid),max(rmid,ma-rmid));
        ans=min(ans,max(max(t1,ma),t+t2+ew[i]));
    }
    printf("%d\n",ans);
}
 

\(O(n)\)做法

结论1：断开的边一定在直径上，否则答案就是直径

结论2：在直径断开后，两子树里的直径有一端点是直径的端点

将直径拉出来变成一个序列,分别求出前缀和后缀的直径和直径中点即可

从左向右遍历，直径长度必然是单调非递减的，由于直径中点一定在原直径上（因为子树直径中属于原直径的部分一定比不属于的部分长），半径的长度也在单调非递减，所以可以尺取求中点

int fa[N],fe[N],fid[N];
int ma,id;
void dfs(int u,int f,int d){
    fa[u]=f;
    if(d>ma) ma=d,id=u;
    erep(u,i) {
        int v=e[i].to;
        if(v==f) continue;
        fe[v]=e[i].w,fid[v]=(i+1)/2+1;
        dfs(v,u,e[i].w+d); 
    }
}
int line[N],d[N],cnt,mk[N];
int len[N];
 
void dfs_findchain(int u,int f,int d){
    ma=max(ma,d);
    erep(u,i) {
        int v=e[i].to;
        if(mk[v]||v==f) continue;
        dfs_findchain(v,u,d+e[i].w);
    }
}//子树的直径一定是由  一段原直径  和 一段直径上点非直径子树的链  相连而得的，所以要预处理这个链长
 
//prefix
int premid[N],prelen[N];
 
//suffix
int sufmid[N],suflen[N];
 
 
 
 
int main(){ 
    n=rd();
    rep(i,2,n) {
        int u=rd(),v=rd(),w=rd();
        AddEdge(u,v,w);
        AddEdge(v,u,w);
    }
    ma=-1;
    dfs(1,0,0);
    int rt=id; 
    ma=-1;
    fa[rt]=0,fe[rt]=0,fid[rt]=0,dfs(rt,0,0);
    int ans=ma;
    while(id) {
        mk[id]=1;
        line[++cnt]=id;
        id=fa[id];
    }
    rep(i,1,cnt/2) swap(line[i],line[cnt-i+1]);
    rep(i,1,cnt) {
        d[i]=fe[line[i]]+d[i-1];
        ma=-1;
        dfs_findchain(line[i],0,0);
        len[i]=ma;
    }
    int p=1;
    rep(i,1,cnt) {
        prelen[i]=max(len[i]+d[i],prelen[i-1]);//求出子树直径长度
        while(p<i && max(prelen[i]-d[p],d[p])>max(prelen[i]-d[p+1],d[p+1]) ) p++;//尺取中点位置
        premid[i]=max(prelen[i]-d[p],d[p]);
    }
    p=cnt+1;
    drep(i,cnt,1) {
        suflen[i]=max(suflen[i+1],len[i]+d[cnt]-d[i]);
        while(p>i+1 && 
  max(suflen[i]-(d[cnt]-d[p-1]),(d[cnt]-d[p-1]))>max(suflen[i]-(d[cnt]-d[p-2]),(d[cnt]-d[p-2]))) p--;
        sufmid[i]=max(suflen[i]-(d[cnt]-d[p-1]),(d[cnt]-d[p-1]));
    }
    rep(i,1,cnt-1)   
        ans=min(ans,max(max(prelen[i],suflen[i+1]),premid[i]+sufmid[i+1]+d[i+1]-d[i]));
    printf("%d\n",ans);
}
 
 

\[\ \]

\[\ \]

T13 2616. SPOJ PERIODNI

笛卡尔树构树+树形dp

其实这题并不是真正用到了笛卡尔树，只是用它的一个性质来方便我们的dp

构树后会形成一棵二叉树，树形满足\(h[lson]>h[u] , h[rson]>h[u]\)，且\(lson<u<rson\)

观察到这样的构树可以使得\(lson,rson\)的\(h[lson] - (h[u]-1),h[rson]- (h[u]-1)\)部分的dp互不影响,可以直接进行转移，最后我们再拿出来，在$h[u]- (h[fa]-1) $这一段空间里放点即可，建议这个放点的方案自己推一下，应该是一个组合数乘一个排列数

关于构树：我只提供\(n^2\)写法，每次查找区间\(L,R\)里的最小值\(h[mid]\),再递归构建\(l,mid-1\),\(mid+1,r\),线性写法网上有很多

int n,m;
int a[N],dp[N][N],sz[N];
int tmp[N];
 
 
 
int po[M]={1,1},Inv[M]={1,1};
 
 
 
int dfs(int l,int r,int f) {
    if(l>r) return 0;
    int u,mi=1e9;
    rep(i,l,r) if(a[i]<mi) mi=a[i],u=i;
    int ls=dfs(l,u-1,u);
    int rs=dfs(u+1,r,u);//找儿子
    sz[u]=0;
    dp[u][0]=1;
    if(ls) {
        rep(i,0,sz[u]) tmp[i]=dp[u][i],dp[u][i]=0;
        rep(i,0,sz[u]) rep(j,0,sz[ls]) dp[u][i+j]=(dp[u][i+j]+1ll*tmp[i]*dp[ls][j]%P)%P;
        sz[u]+=sz[ls];
    }
    if(rs) {
        rep(i,0,sz[u]) tmp[i]=dp[u][i],dp[u][i]=0;
        rep(i,0,sz[u]) rep(j,0,sz[rs]) dp[u][i+j]=(dp[u][i+j]+1ll*tmp[i]*dp[rs][j]%P)%P;
        sz[u]+=sz[rs];
    }//合并子树信息
    sz[u]++;
    int d=a[u]-a[f];
    drep(i,sz[u],1) {
        drep(j,i-1,max(0,i-d)) {
            dp[u][i]=(dp[u][i]+1ll*dp[u][j]*po[sz[u]-j]%P*Inv[i-j]%P*Inv[sz[u]-i]%P*po[d]%P*Inv[d-(i-j)]%P)%P;
        }
    }//在剩下的空间里放点
    return u;
}
 
int main(){
    rep(i,2,M-1) {
        po[i]=1ll*po[i-1]*i%P;
        Inv[i]=1ll*(P-P/i)*Inv[P%i]%P;
    }
    rep(i,2,M-1)  Inv[i]=1ll*Inv[i]*Inv[i-1]%P;
    n=rd(),m=rd();
    rep(i,1,n) a[i]=rd();
    printf("%d\n",dp[dfs(1,n,0)][m]);
}