MCMC方法

这篇文章

https://zhuanlan.zhihu.com/p/250146007

其实随机算法分为两类：蒙特卡罗方法和拉斯维加斯方法，蒙特卡罗方法指的是算法的时间复杂度固定，然而结果有一定几率失败，采样越多结果越好。拉斯维加斯方法指的是算法一定成功，然而运行时间是概率的。

• 不可约：每个状态都能去到。
• 非周期：返回时间公约数是1。
• 正常返：离开此状态有限步一定能回来。迟早会回来。
• 零常返：离开此状态能回来，但需要无穷多步。
• 非常返：离开此状态有限步不一定回得来。
• 遍历定理：不可约，非周期，正常返  有唯一的平稳分布。

 

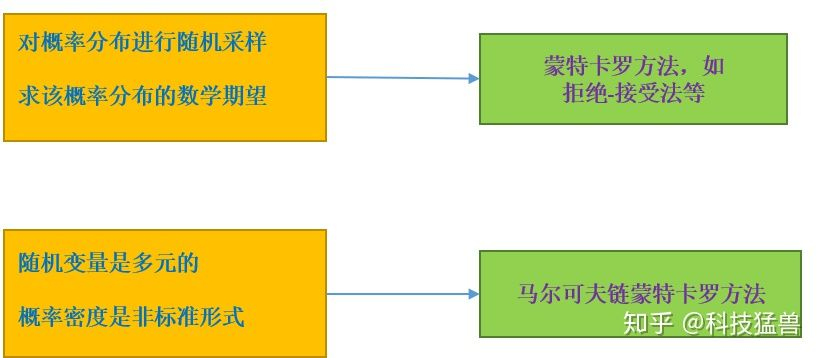
常用的马尔可夫链蒙特卡罗法有Metropolis-Hastings算法、吉布斯抽样。

 

 

MCMC算法的一般流程是：先给定目标分布完成采样过程，若目标分布是一维的，就用M-H采样方法；若目标分布是多维的，就用Gibbs采样方法。采样结束之后，蒙特卡罗方法来用样本集模拟求和，求出目标变量(期望等)的统计值作为估计值。这套思路被应用于概率分布的估计、定积分的近似计算、最优化问题的近似求解等问题，特别是被应用于统计学习中概率模型的学习与推理，是重要的统计学习计算方法。

 

 

下面这篇文章讲得也挺好，我觉得代码部分比上面的好一些

https://blog.csdn.net/weixin_39953236/article/details/111369770?spm=1001.2101.3001.6650.7&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-7.pc_relevant_default&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-7.pc_relevant_default&utm_relevant_index=10

 

 

 

MH算法

# -*- coding:utf-8 -*-
 
import random
import numpy as np
import matplotlib.pyplot as plt
 
 
def mh(q, p, m, n):
    # randomize a number
    x = random.uniform(0.1, 1)
    for t in range(0, m+n):
        x_sample = q.sample(x)
        try:
            accept_prob = min(1, p.prob(x_sample)*q.prob(x_sample, x)/(p.prob(x)*q.prob(x, x_sample)))
        except:
            accept_prob = 0
 
        u = random.uniform(0, 1)
 
        if u < accept_prob:
            x = x_sample
 
        if t >= m:
            yield x
 
 
class Exponential(object):
    def __init__(self, scale):
        self.scale = scale
        self.lam = 1.0 / scale
 
    def prob(self, x):
        if x <= 0:
            raise Exception("The sample shouldn't be less than zero")
 
        result = self.lam * np.exp(-x * self.lam)
        return result
 
    def sample(self, num):
        sample = np.random.exponential(self.scale, num)
        return sample
 
 
# 假设我们的目标概率密度函数p1(x)是指数概率密度函数
scale = 5
p1 = Exponential(scale)
 
 
class Norm():
    def __init__(self, mean, std):
        self.mean = mean
        self.sigma = std
 
    def prob(self, x):
        return np.exp(-(x - self.mean) ** 2 / (2 * self.sigma ** 2.0)) * 1.0 / (np.sqrt(2 * np.pi) * self.sigma)
 
    def sample(self, num):
        sample = np.random.normal(self.mean, self.sigma, size=num)
        return sample
 
# 假设我们的目标概率密度函数p1(x)是均值方差分别为3,2的正态分布
p2 = Norm(3, 2)
 
 
class Transition():
    def __init__(self, sigma):
        self.sigma = sigma
 
    def sample(self, cur_mean):
        cur_sample = np.random.normal(cur_mean, scale=self.sigma, size=1)[0]
        return cur_sample
 
    def prob(self, mean, x):
        return np.exp(-(x-mean)**2/(2*self.sigma**2.0)) * 1.0/(np.sqrt(2 * np.pi)*self.sigma)
 
 
# 假设我们的转移核方差为10的正态分布
q = Transition(10)
 
m = 100
n = 100000 # 采样个数
 
simulate_samples_p1 = [li for li in mh(q, p1, m, n)]
 
plt.subplot(2,2,1)
plt.hist(simulate_samples_p1, 100)
plt.title("Simulated X ~ Exponential(1/5)")
 
samples = p1.sample(n)
plt.subplot(2,2,2)
plt.hist(samples, 100)
plt.title("True X ~ Exponential(1/5)")
 
simulate_samples_p2 = [li for li in mh(q, p2, m, n)]
plt.subplot(2,2,3)
plt.hist(simulate_samples_p2, 50)
plt.title("Simulated X ~ N(3,2)")
 
 
samples = p2.sample(n)
plt.subplot(2,2,4)
plt.hist(samples, 50)
plt.title("True X ~ N(3,2)")
 
plt.suptitle("Transition Kernel N(0,10)simulation results")
plt.show()

Gibbs采样

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
 
 
class Transition():
    def __init__(self, mean, cov):
        self.mean = mean
        self.sigmas = []
        for i in range(K):
            self.sigmas.append(np.sqrt(cov[i][i]))
        self.rho = cov[0][1]/(self.sigmas[0] * self.sigmas[1])
 
    def sample(self, id1, id2_list, x2_list):
        id2 = id2_list[0]  # only consider two dimension
        x2 = x2_list[0]  # only consider two dimension
        cur_mean = self.mean[id1] + self.rho*self.sigmas[id1]/self.sigmas[id2] * (x2-self.mean[id2])
        cur_sigma = (1-self.rho**2) * self.sigmas[id1]**2
        return np.random.normal(cur_mean, scale=cur_sigma, size=1)[0]
 
 
def gibbs(p, m, n):
    # randomize a number
    x = np.random.rand(K)
    for t in range(0, m+n):
        for j in range(K):
            total_indexes = list(range(K))
            total_indexes.remove(j)
            left_x = x[total_indexes]
            x[j] = p.sample(j, total_indexes, left_x)
 
        if t >= m:
            yield x
 
 
mean = [5, 8]
cov = [[1, 0.5], [0.5, 1]]
K = len(mean)
q = Transition(mean, cov)
m = 100
n = 1000
 
gib = gibbs(q, m, n)
 
simulated_samples = []
 
x_samples = []
y_samples = []
for li in gib:
    x_samples.append(li[0])
    y_samples.append(li[1])
 
 
fig = plt.figure()
ax = fig.add_subplot(131, projection='3d')
 
hist, xedges, yedges = np.histogram2d(x_samples, y_samples, bins=100, range=[[0,10],[0,16]])
xpos, ypos = np.meshgrid(xedges[:-1], yedges[:-1])
xpos = xpos.ravel()
ypos = ypos.ravel()
zpos = 0
 
dx = xedges[1] - xedges[0]
dy = yedges[1] - yedges[0]
dz = hist.flatten()
 
ax.bar3d(xpos, ypos, zpos, dx, dy, dz, zsort='average')
 
ax = fig.add_subplot(132)
ax.hist(x_samples, bins=50)
ax.set_title("Simulated on dim1")
 
ax = fig.add_subplot(133)
ax.hist(y_samples, bins=50)
ax.set_title("Simulated on dim2")
plt.show()