矢量线的一种栅格化算法

目录

• 1. 概述
  • 1.1. 已知算法
  • 1.2. 本文算法
• 2. 实现
• 3. 参考

1. 概述

1.1. 已知算法

将一条线段栅格化的最简单的算法思路是根据其斜率，按X或Y方向步进取值：

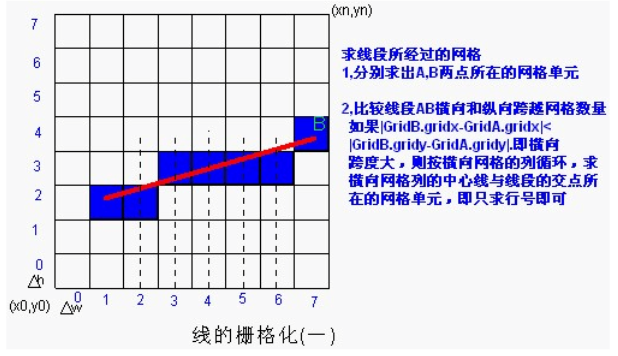
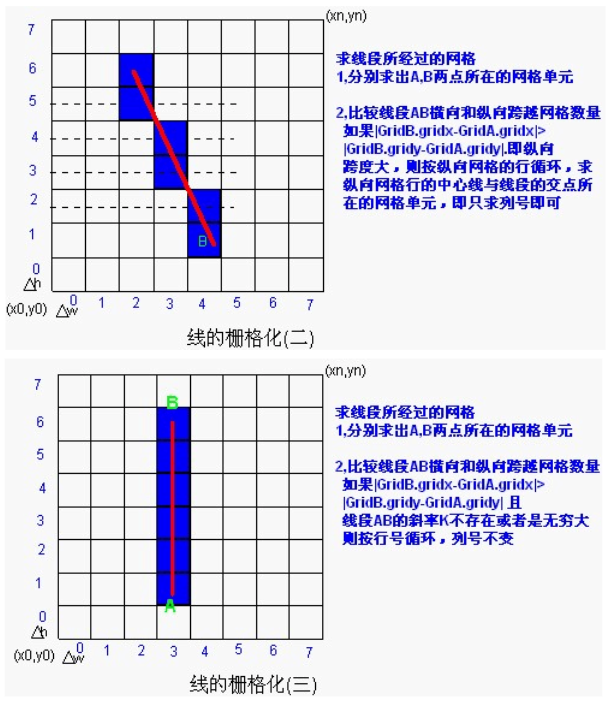
除此之外还有一种算法是利用计算机图形学中绘制直线的Bresenham算法，这种算法的效率很高，原理就是用遍历的办法规避乘法和除法，只用加减法就能完成线段的栅格化。

1.2. 本文算法

上述两种算法有个问题就是都要经过一系列繁复的判断，才能得到比较严密的结果，所以我并没有采用。我这里采用的算法也是逐渐步进求值的办法，只不过不再沿着X或者Y方向求值，而是沿着射线方向步进。这里的射线指的是从线段的起点开始，以1像素为步进单位，步进到线段的终点。因为线段的方向性问题，步进得到的点总会有重复的值，最后再进行去重操作即可。

算法过程简述如下：

1. 设线段的起点为(O)，终点为(E)，则方向向量为(D=E-O)；
2. 线段的长度L为向量(D)的模。以0为初值，L为终值，以1为步进值建立一个for循环，每次取的长度为d;
3. 令(t=d/L)，则线段上相应的点为(P=O+tD)。这个公式是根据射线向量方程推导出来的，可以参看这篇文章《已知线段上某点与起点的距离，求该点的坐标》;
4. 将取的点都保存到容器中;
5. 对容器中的点进行去重操作。

最终得到的点即为直线栅格化后的点。

2. 实现

具体的C++实现代码如下：

#include <iostream>
#include <vector>

using namespace std;

const double EPSILON = 0.000001;

// 2D Point
struct Vector2d
{
public:
	Vector2d()
	{
	}

	Vector2d(double dx, double dy)
	{
		x = dx;
		y = dy;
	}

	// 矢量赋值
	void set(double dx, double dy)
	{
		x = dx;
		y = dy;
	}

	// 矢量相加
	Vector2d operator + (const Vector2d& v) const
	{
		return Vector2d(x + v.x, y + v.y);
	}

	// 矢量相减
	Vector2d operator - (const Vector2d& v) const
	{
		return Vector2d(x - v.x, y - v.y);
	}

	//矢量数乘
	Vector2d Scalar(double c) const
	{
		return Vector2d(c*x, c*y);
	}

	// 矢量点积
	double Dot(const Vector2d& v) const
	{
		return x * v.x + y * v.y;
	}

	//向量的模
	double Mod() const
	{
		return sqrt(x * x + y * y);
	}

	bool Equel(const Vector2d& v) const
	{
		if (abs(x - v.x) < EPSILON && abs(y - v.y) < EPSILON)
		{
			return true;
		}
		return false;
	}

	double x, y;
};

//栅格化一条线段
void RasterLine(std::pair<Vector2d, Vector2d> line, std::vector<Vector2d>& linePointList)
{
	Vector2d vecLine = line.second - line.first;
	double lineLength = vecLine.Mod();
	double step = 1.0;

	//根据距离逐步取
	vector<Vector2d> tmpPointList;
	double curLength = 0;
	while (curLength < lineLength)
	{
		curLength = curLength + step;
		Vector2d P = line.first + vecLine.Scalar(curLength / lineLength);
		P.x = (int)(P.x + 0.5);
		P.y = (int)(P.y + 0.5);
		tmpPointList.push_back(P);
	}

	//与最后一个值比较，去重
	linePointList.push_back(line.first);
	for (size_t i = 0; i < tmpPointList.size(); i++)
	{
		//与最后一个值比较，去重
		if (!tmpPointList[i].Equel(linePointList[linePointList.size() - 1]))
		{
			linePointList.push_back(tmpPointList[i]);
		}
	}

	if (!linePointList[linePointList.size() - 1].Equel(line.second))
	{
		linePointList.push_back(line.second);
	}
}


int main()
{
	Vector2d O(30, 60);
	Vector2d E(88, 104);
	std::pair<Vector2d, Vector2d> line(O, E);

	vector<Vector2d> linePointList;
	RasterLine(line, linePointList);

	for (size_t i = 0; i < linePointList.size(); i++)
	{
		cout << linePointList[i].x << ',' << linePointList[i].y << '	';
	}
}

其运行的结果如下：

3. 参考

[1].矢量数据栅格化
[2].Bresenham算法