假设小兔的棋盘是 8 × 8 的 ( 当然你也可以假设是其他 )。如下图:
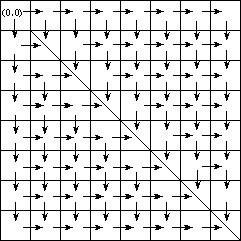
箭头方向表示从该格子下一步能去的格子。因为不能穿越对角线,所有对角线上的格子只有进去的箭头,没有出来的箭头。
观察上图你就可以发现,其实这是一张关于对角线对称的图。所有我们只要求一个方向的值,然后乘以2即可。
我们就拿下三角来考虑。不难发现,所有在0列上的格子,路径数都是 1 (只能从上面过来)。
而其他格子则都是由上、左两个方向过来,即:f(i, j) = f(i - 1, j) + f(i, j - 1);
另外f(i, i) = f(i, j - 1) 或者 f(i, i) = f( i-1, j ) ;
#include"stdio.h"
int main( )
{
int i,j,n,m=0;
__int64 num[40][40];
for(i=1;i<=40;i++)
num[0][i]=1;
for(i=1;i<40;i++)
{
for(j=i;j<40;j++)
{
if(i==j)
num[i][j]=num[i-1][j];
else
num[i][j]=num[i-1][j]+num[i][j-1];
}
}
while(scanf("%d",&n)==1&&n!=-1)
{
m++;
printf("%d %d %I64d\n",m,n,2*num[n][n]);
}
return 0;
}
