Wasserstein GAN (WGAN)
在一些情况下,用 JS散度来衡量两个分布的远近并不适合:
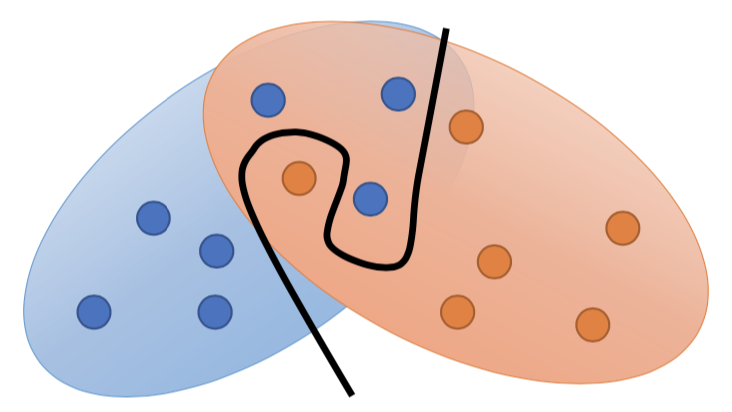
1. 数据是高维空间中的低维流形(manifold),两个分布在高维空间中的 overlap 少到可以忽略。

2. 由于 sampling 的局限性,即使两个分布之间真的存在一定的 overlap,但如果采样的数据不够多的话,可能实际上并不能体现出来。
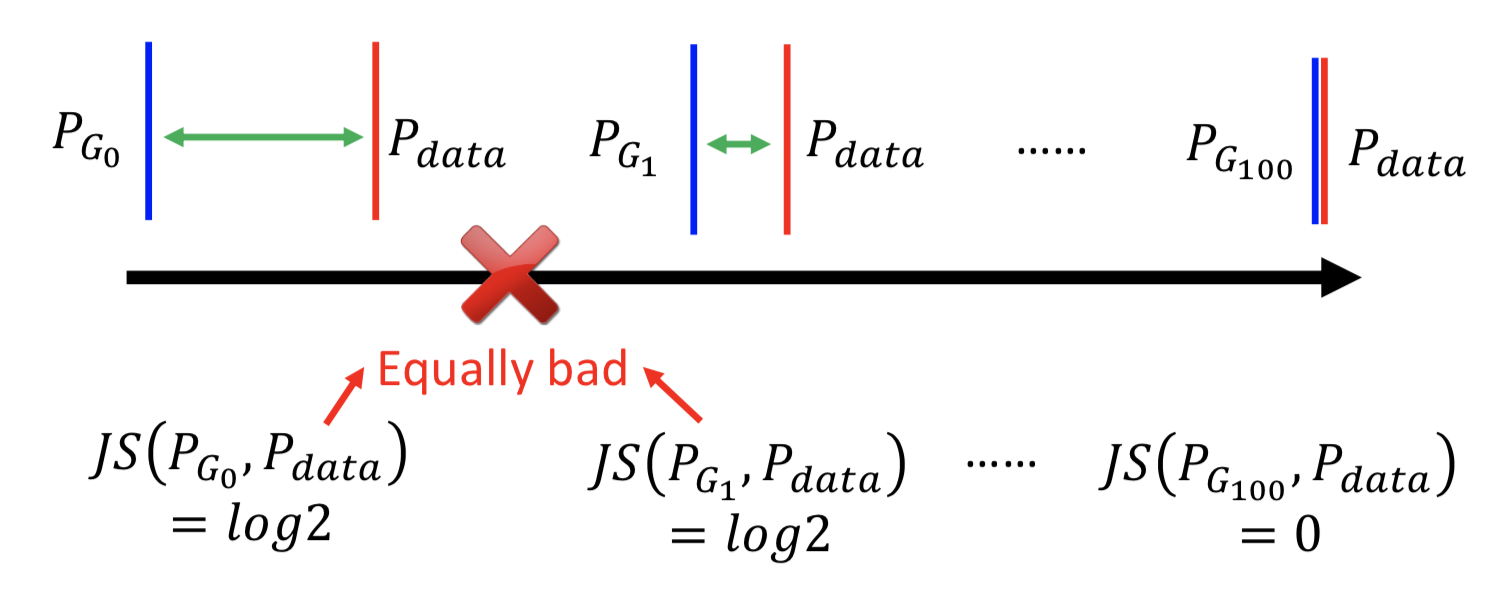
在这种情况,GAN 训练过程中用JS散度来衡量分布之间的距离,即使已经很接近但是没有重合,还是会计算为常数 2log2,那在训练 D 的过程中 loss 就没有改变,梯度也就一直不变,整个 GAN 的 minmax 训练就变得困难。
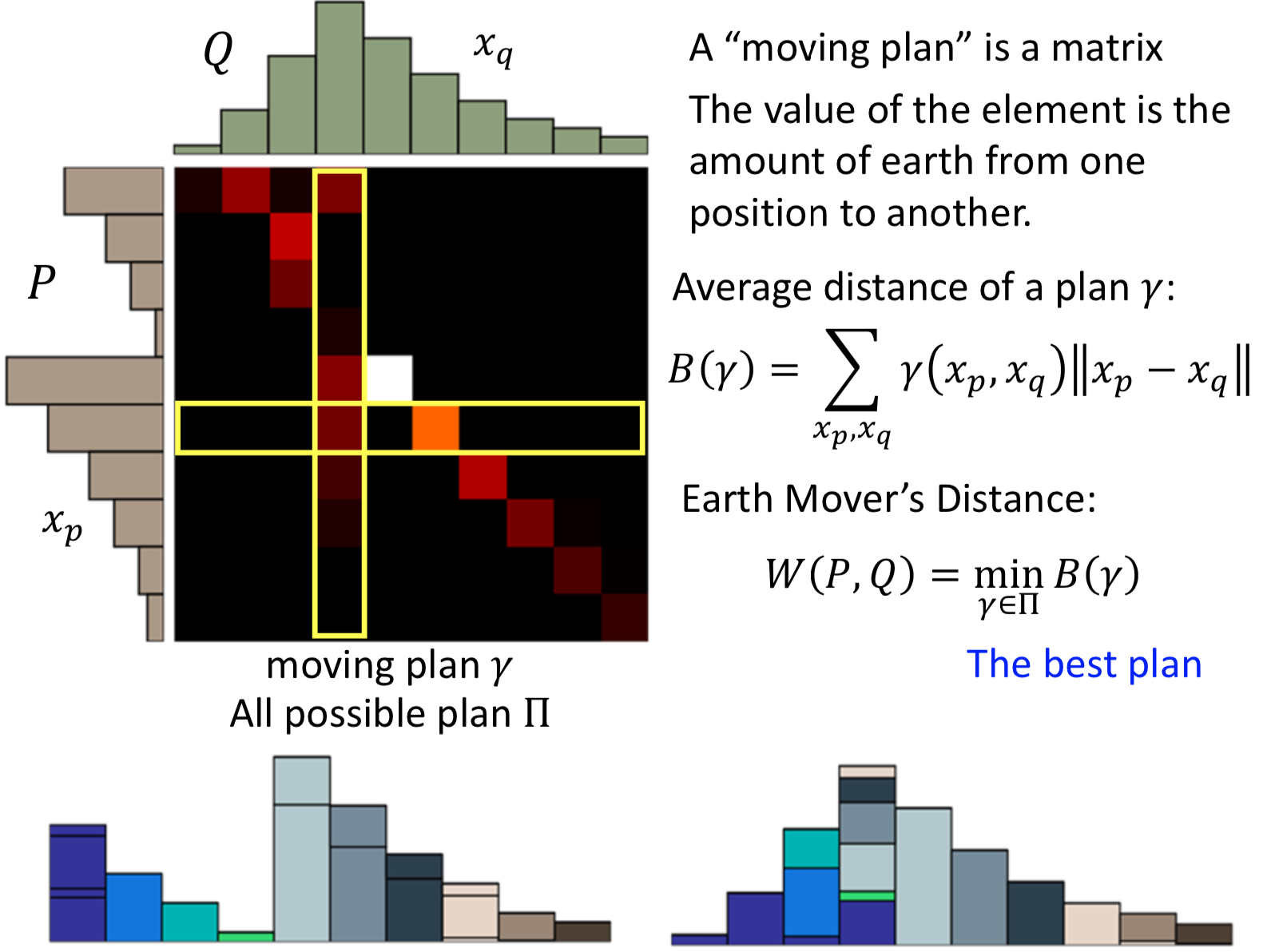
Earth Mover’s Distance
不用JS散度,用 The Earth Mover's Distance http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/RUBNER/emd.htm
所有的 moving plan 中平均距离最小的
好处就是,即使两个分布没有overlap,还是能够体现出距离远近。怎么应用到 GAN 的目标函数中呢?
把 D 的最后一层的 sigmoid 函数拿掉,让 D 变成一个 real-value function ,但必须是 1-Lipschitz 连续的。(就是要让这个函数平滑,避免无法收敛的情况)

Lipschitz 函数的定义,K=1 的时候就是 1-Lipschitz 函数,y的变化总是比x的变化要小,就会比较平滑。
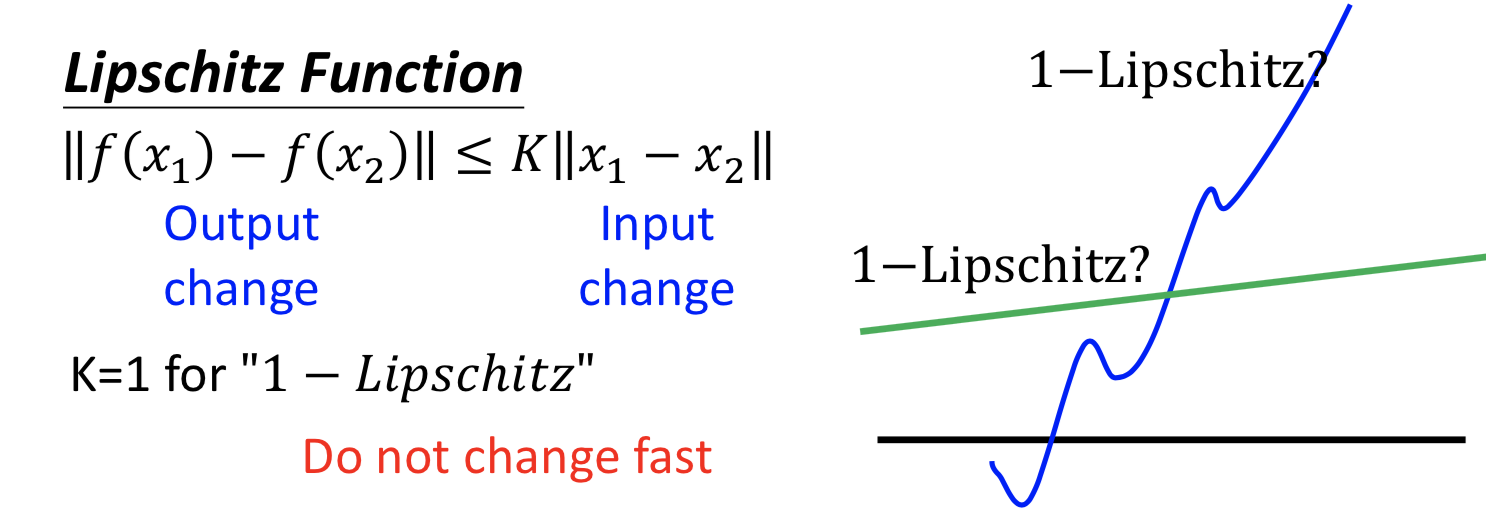
实施 1-Lipschitz 约束的方法:
1. weight clipping:Force the parameters w between c and -c. After parameter update, if w > c, w = c; if w < -c, w = -c. 但是这个做法比较粗糙,会导致 weights 大部分都直接被截在+c和-c,相当于减弱了NN的拟合能力。
2. gradient penalty(WGAN-GP):A differentiable function is 1-Lipschitz if and only if it has gradients with norm less than or equal to 1 everywhere. 这个做法就是从 1-Lipschitz 函数定义出发了,但没办法真的做到对 x 积分,所以通过在P_data 和 P_G 之间随机插值采样来实现 from P_penalty 对里面的 max 函数求期望,近似积分项。
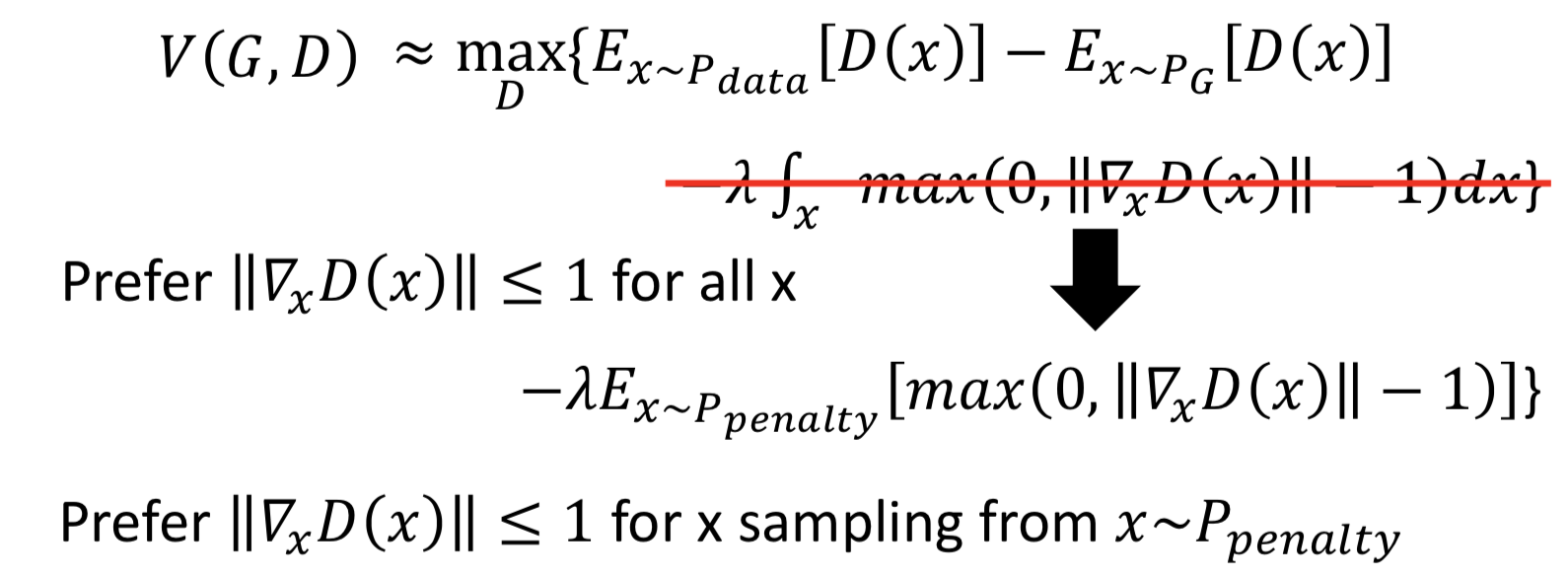
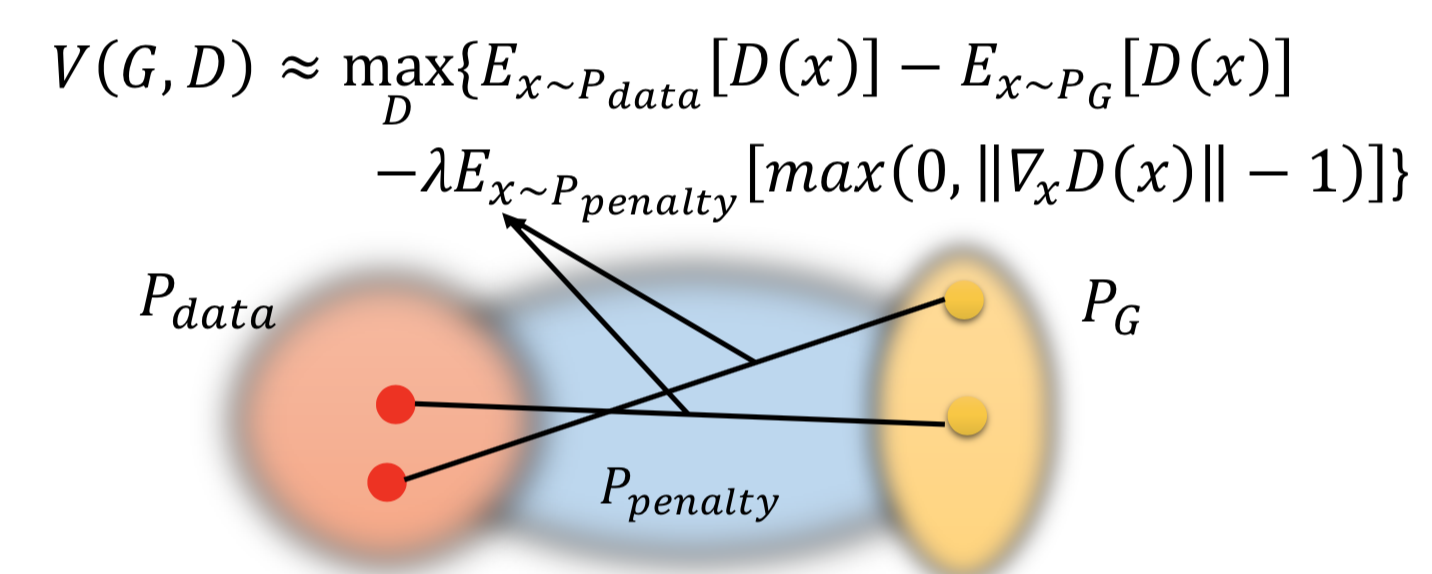
为什么是在 P_data 和 P_G 之间插值呢?
因为论文中表示,这样做效果好。而且这个区域的点能够反映 how P_G moves to P_data,其他的 region 反正 P_G 也走不到,干脆就不管它。
实际做的时候,gradient 的 norm 大于或小于 1 都会惩罚,原因也是做实验效果好:
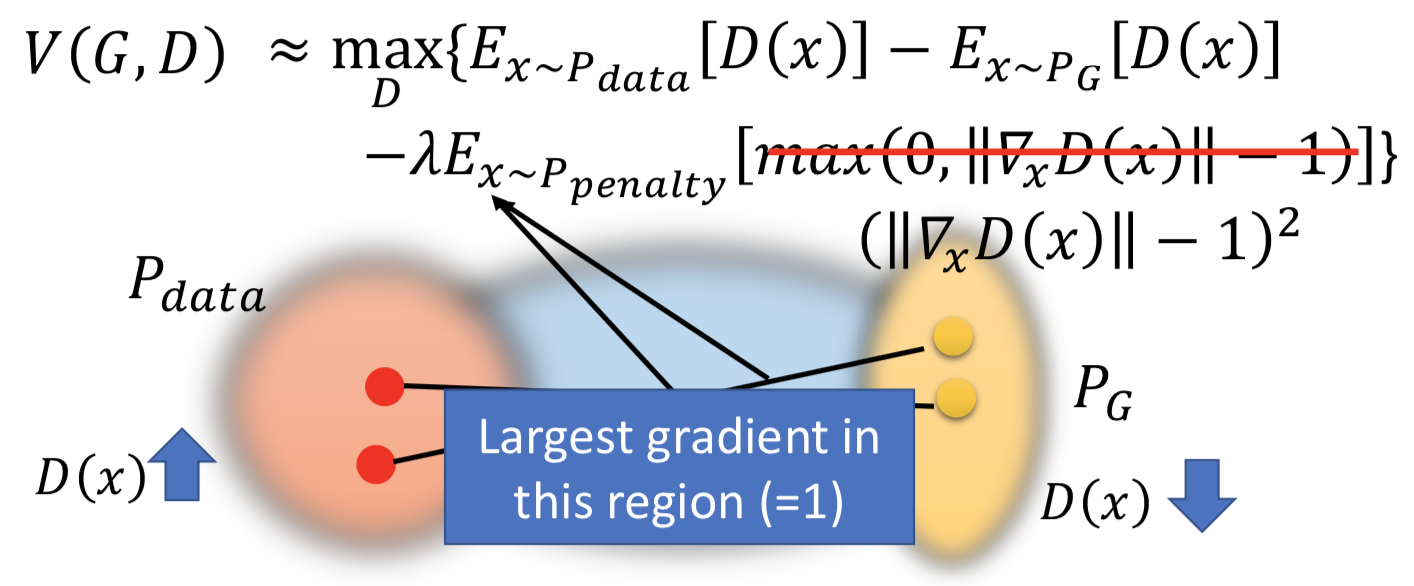
3. Spectrum Norm
总结一下,WGAN:

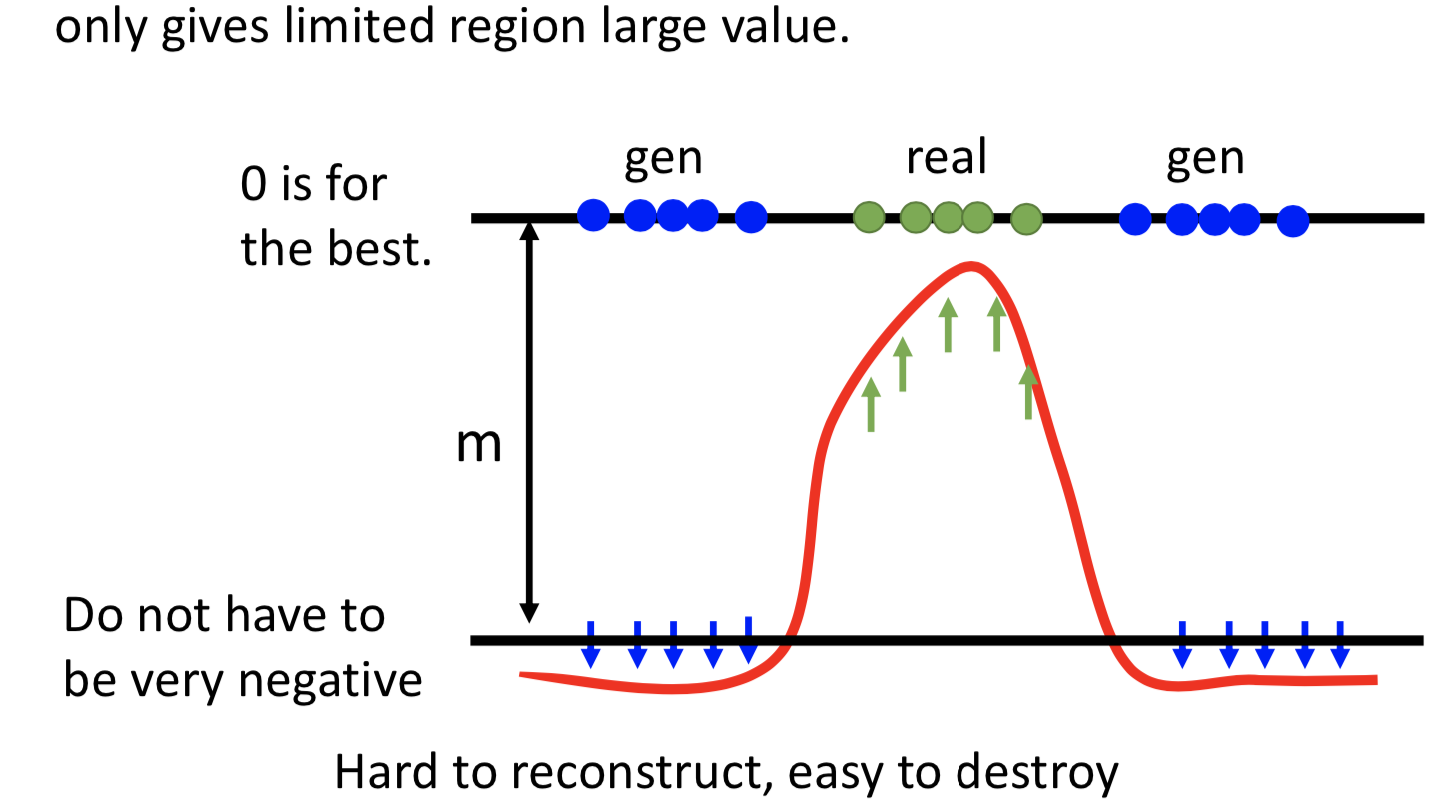
Energy-based GAN (EBGAN)
用一个 ae 来当作 discriminator,generator不改变。不用二分类器来做判别,而是依据自编码器的 negative reconstruction error 。这样做的好处是 ae 可以事先单独拿出来只用real data 就能 pre-train 。
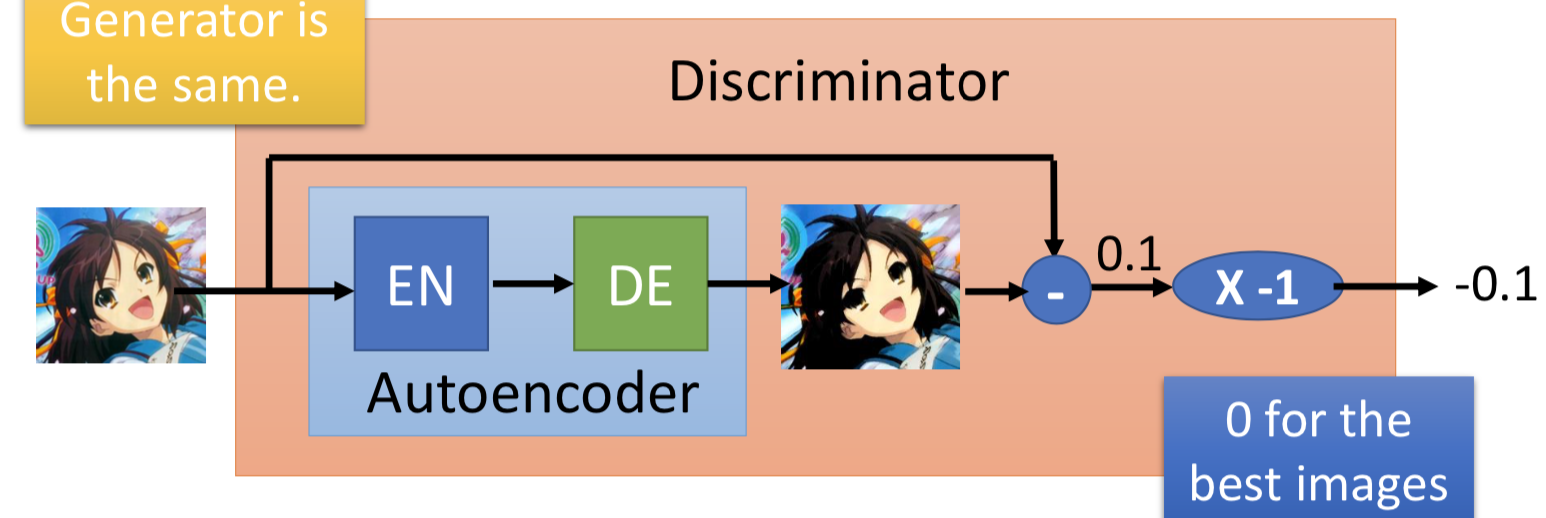
另外一个要特别注意的是,并不是要让 generated data 的 reconstruction error 越大越好,所以要设置一个margin,generated data 的 reconstruction error 小于这个阈值就好