
树:n(n>=0)个节点的有限集。有且只有一个root,子树的个数没有限制但互不相交。结点拥有的子树个数就是该结点的度(Degree)。度为0的是叶结点,除根结点和叶结点,其他的是内部结点。结点的层次(Level)从根结点开始从1计数,树中结点的最大深度称为树的深度(Depth)。树中结点的子树看成从左到右有次序不能互换的,称为有序树。多棵不相交的树构成森林。
树的存储结构

1. 双亲表示法(结点中存指针指向双亲,但要找某结点的孩子要遍历整棵树,所以可以加上指针指向孩子)
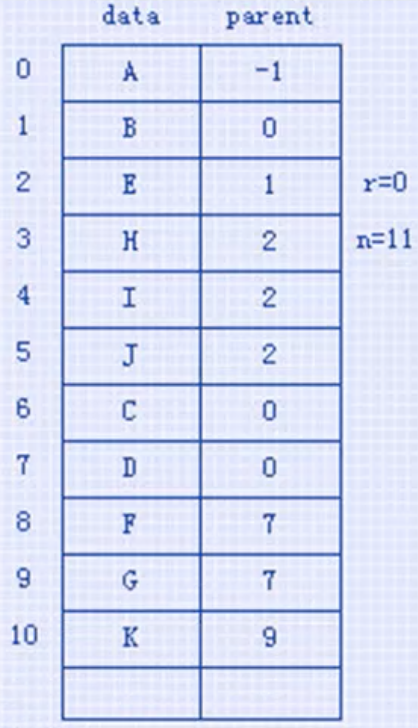

2. 孩子表示法(数组+链表,减少空间浪费也便于维护。数组保存头指针,通过链表记录所有孩子)
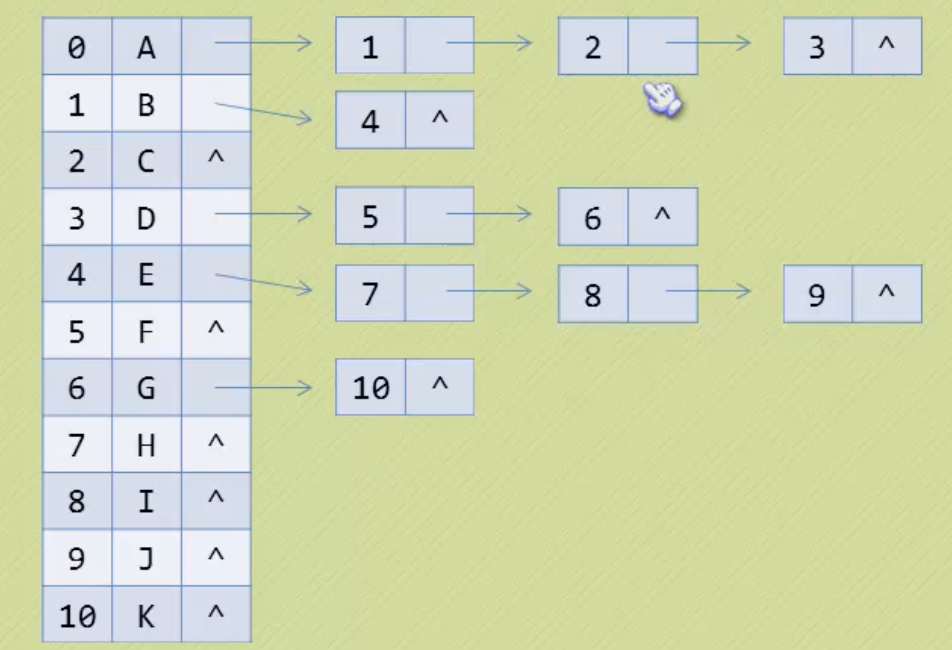
3. 双亲孩子表示法(进一步完善)

4. 孩子兄弟表示法(类似以上)
二叉树
每个结点最多有两颗子树,左右有顺序,即使只有一棵树也要区分左右。二叉树的五种基本形态:

斜树:只往一边拓展。
满二叉树:所有结点都有左右子树,并且叶子都在同一层上。
完全二叉树:按层序编号,每个结点 i 与同样深度的满二叉树中编号为 i 的结点位置完全相同,称为完全二叉树。叶子只能出现在最下两层,最下层叶子一定集中在左部连续位置,倒数第二层叶子一定集中在右部。
二叉树的性质:
1. 二叉树第 i 层至多 2i-1 个结点
2. 深度为k的二叉树至多有2k - 1 个结点
3.如果叶结点数为n0,度为2的结点数为n2,则n0 = n2 + 1。
设度为1的结点数为n1,那么总结点数n = n0+n1+n2;连接数总是等于n-1,并且等于n1 + 2*n2,所以n0 = n2 + 1
4. n个结点的完全二叉树的深度为 floor( log2(n) ) + 1。(向下取整再加1)
5. 已知 4 的性质,对结点按层序编号,对任意结点 i 具有性质:
如果 i=1,则结点 i 是根节点,如果i>1, 双亲结点是floor(i/2);
如果2i > n,则结点i无左孩子(i为叶子结点);否则其左孩子是结点2i
如果2i+1 >n,则结点i无右孩子;否则其右孩子结点是2i+1
二叉树的存储结构:
顺序存储结构,完全二叉树只用数组就能表示其结点之间的逻辑关系;一般二叉树就把不存在的结点标记一下,但会造成空间浪费。
链式存储结构,一个数据域 + 两个指针域。更常用。
二叉树的常见操作
遍历,基本上是其他操作的基础。二叉树操作非常适合用递归实现。
class Node(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
层次遍历(一层一层从左到右)、前序遍历(根左右)、中序遍历(左根右)、后序遍历(左右根)
层次:bfs 或者 dfs都行,前者用队列实现,后者用栈(递归)实现。
当前最高的层数就是输出列表的长度 len(result):
比较访问节点所在的层次 level 和当前最高层次 len(result) 的大小,如果相等就向 result 添加一个空 list 存新的一层的节点;
将当前层的节点插到对应层的列表中;
递归非空的孩子节点。
这里递归做法的本质还是 dfs,巧妙的在于会根据记录的 level 判断加到哪个层次,直接按level往对应的位置塞。
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
result = []
if not root:
return result
def helper(node, level):
if level == len(result): # 如果节点node的层次和当前最高层次相同,就增加一个空list存下一层节点
result.append([])
result[level].append(node.val) # 存储当前节点值
if node.left:
helper(node.left, level+1) # 存左孩子到下一层
if node.right:
helper(node.right, level+1) # 存右孩子到下一层
helper(root, 0)
return result
典型的bfs,使用队列先进先出的特性,每层节点入队,输出的时候再令左右孩子入队,这样就会排在上一层和本层的更左部节点之后,实现层次遍历。
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
result = []
if not root:
return result
q = [root,] # 模拟队列
while q:
tmp = [] # 存储当前一层的节点值
for i in range(len(q)): # 同层节点依次出队+左右孩子入队,用for控制刚好一层全部出完
node = q.pop(0)
tmp.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
result.append(tmp) # tmp存这一层的节点值,q在每一轮的这个时候都只存下一层自左向右的节点
return result
前序:递归;栈(涉及到回溯)
创建二叉树时常用前序。
result = []
def PreOrdTrav(root):
if root != None:
result.append(root.val)
PreOrdTrav(root.left)
PreOrdTrav(root.right)
根据根左右的遍历顺序,要从根节点开始一直向左考察,这期间考察过的结点依次入栈,直到左子树为空的结点,且栈非空。弹出栈顶元素,考察该元素的右子树。当遍历到最后一个结点的时候,左右子树均为空且栈也空。

result = []
def PreOrdTraval(root):
if root != None:
treeStack = [] # 栈,按遍历顺序存放所有子树的根
pNode = root
while pNode or treeStack: # 遍历到最后一个结点时,左右子树和栈都空(pNode被赋None)
while pNode: # 一直向左考察并入栈,直到入栈了左子树为空的父结点
treeStack.append(pNode)
result.append(pNode.val)
pNode = pNode.left
if treeStack: # 考察栈顶元素的右子树,如果栈空则没有右子树需要考察
pNode = treeStack.pop()
pNode = pNode.right # 下一轮从这个右子树的根开始先序遍历
中序:递归;栈
result = []
def InOrdTrav(root):
if root != None:
InOrdTrav(root.left)
result.append(root.val)
InOrdTrav(root.right)
和先序类似,区别在于考察到当前结点时,并不立刻输出该结点,而是当考察结点为空,从栈中弹出到时候才输出。(永远要先考虑左子树,只有左子树为空时才输出根结点)
result = []
def InOrdTrav(root):
if root != None:
treeStack = []
pNode = root
while pNode or treeStack:
while pNode: # 一直向左考察并入栈,直到左子树为空的父节点,考察其右子树
treeStack.append(pNode)
pNode = pNode.left
if treeStack:
pNode = treeStack.pop() # 准备考察左子树为空的父节点的右子树之前,再输出节点值
result.append(pNode.val)
pNode = pNode.right
后序:递归;栈
result = []
def PostOrdTrav(root):
if root != None:
PostOrdTrav(root.left)
PostOrdTrav(root.right)
result.append(root.val)
后序遍历的迭代实现稍微困难一些,从栈中pop出来一个父节点的时候,决定是否可以它时,要先考虑其左右结点是否都已经遍历完成。所以要设置一个lastVisit游标。若lastVisit等于当前考查节点的右子树(或者考察节点没有右子树),表示该节点的左右子树都已经遍历完成(因为先一直向左找到左子树为空的节点了),则可以输出当前节点,并把lastVisit节点设置成当前节点,将当前游标节点pNode设置为空(下一轮就可以直接访问上一个父节点)。否则,不能输出当前结点,需要接着整体考虑其右子树。
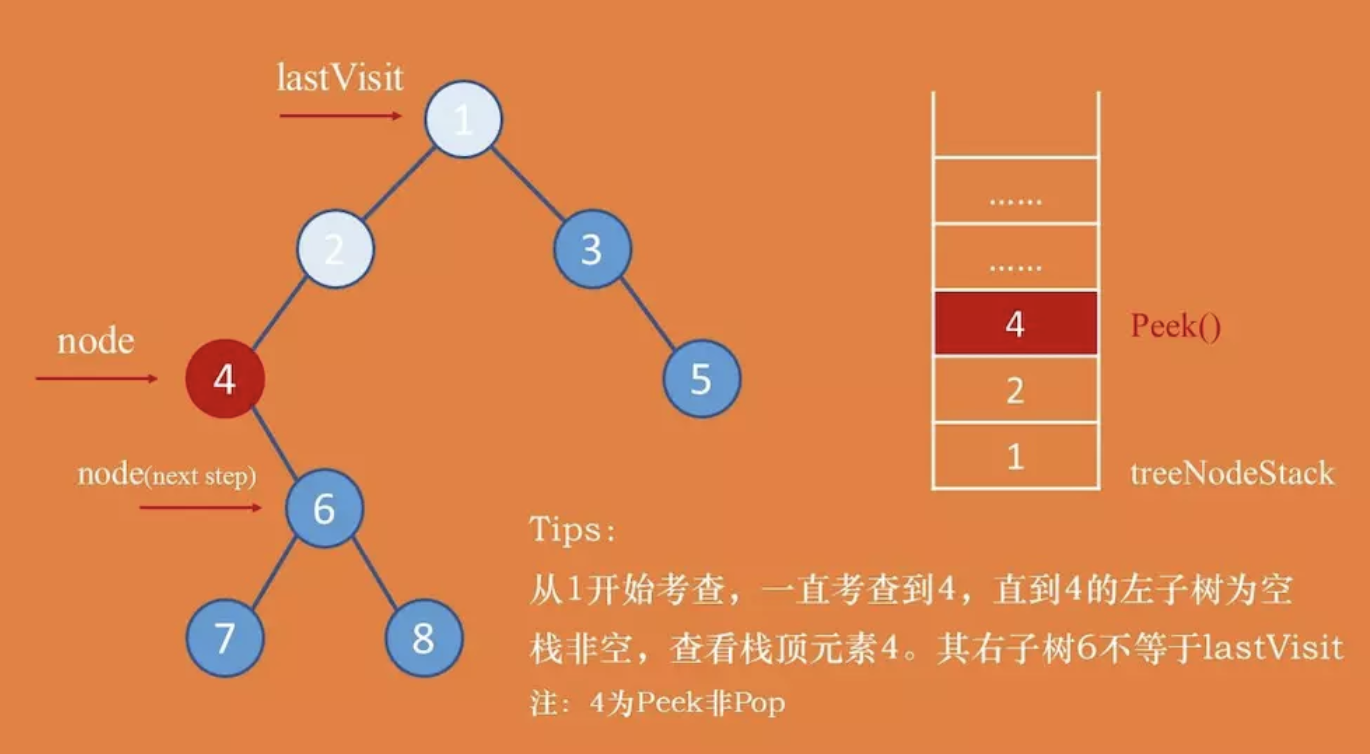


result = []
def PostOrdTrav(root):
if root != None:
treeStack = []
pNode = root
lastVisit = root
while pNode or treeStack:
while pNode: # 一直向左考察并入栈,找到左子树为空的结点为止
treeStack.append(pNode)
pNode = pNode.left
pNode = treeStack[-1] # 查看当前栈顶元素,如果右子树空或已经输出,则可以输出当前结点的值
if pNode.right == None or lastVisit == pNode.right:
result.append(pNode.val)
treeStack.pop()
lastVisit = pNode
pNode = None # 把pNode赋为None,下一轮直接看当前输出节点的父节点能不能输出(不需要再向左遍历了)
else:
pNode = pNode.right # 否则的话暂时不能输出当前节点值,要进入下一轮继续考察其右子树
关于二叉树的前中后序的迭代实现,一篇比较直观易懂的博客、图片来源:https://www.jianshu.com/p/456af5480cee
把二叉树中所有节点的值加1
def plusOne(root):
if root is None:
return
root.val += 1
plusOne(root.left)
plusOne(root.right)
判断两颗二叉树是否完全相同
def isSame(root1, root2):
if root1 is None and root2 is None:
return True
if root1 is None or root2 is None:
return False
if root1.val != root2.val:
return False
return isSame(root1.left, root2.left) and isSame(root1.right, root2.right)
二叉搜索树(二叉排序树)BST
插入和删除的效率不错,同时查找的效率也很高的算法。
满足:
左子树不为空时,左子树上所有节点的值小于它的根节点的值;
右子树不为空时,右子树上所有节点的值大于它的根节点的值;
左右子树也分别为二叉排序树。
中序遍历二叉排序树,就能得到一个有序序列。二叉树结构有利于插入删除操作。
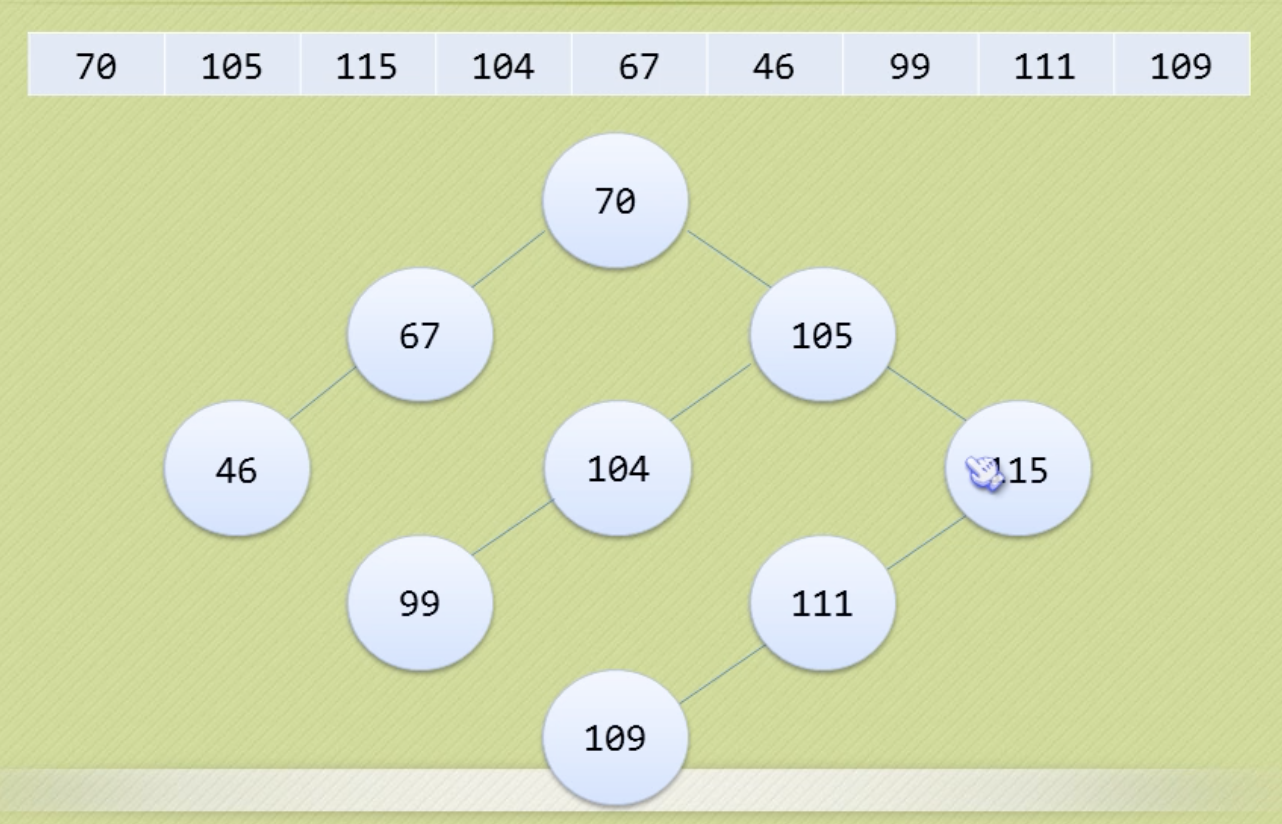
判断二叉搜索树的合法性
BST中一个节点要合法,不能只和其左右孩子节点比较大小,而是左右子树所有节点,所以在递归的时候限制当前节点node的上下界,越界的节点即不合法。
def isValidBST(root):
return helper(root, None, None)
def helper(node, min_node, max_node):
if root is None:
return True
if min_node and node.val <= min_node.val:
return False
if max_node and node.val >= max_node.val:
return False
return helper(node.left, min_node, node) and helper(node.right, node, max_node)
查找、插入、删除
class Node:
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
class BST:
def __init__(self, node_list):
self.root = Node(node_list[0])
for data in node_list[1:]:
self.insert(data) # 插入元素创建二叉排序树
# 搜索
def search(self, node, parent, key): # 开始搜索的节点node,其父节点parent,关键字key
if node is None:
return False, node, parent
if node.data == key:
return True, node, parent # 如果当前节点的val等于key,返回搜索结果
if node.data > key:
return self.search(node.lchild, node, data) # 如果当前节点的val大于key,去左子树搜索
else:
return self.search(node.rchild, node, data) # 如果当前节点的val大于key,去右子树搜索
# 插入
def insert(self, data):
flag, n, p = self.search(self.root, self.root, data)
if not flag: # 如果二叉排序中不存在待插入节点,找到新节点的父节点
new_node = Node(data) # 创建新节点
if data > p.data: # 判断新节点是父节点的左孩子还是右孩子,然后插入即可
p.rchild = new_node
else:
p.lchild = new_node
# 删除
def delete(self, root, data):
flag, n, p = self.search(root, root, data)
if flag is False:
print("无该关键字,删除失败")
else:
if n.lchild is None: # 若待删节点n的左子树为空
if n == p.lchild: # 若n是其父节点p的左子树,则n的右子树变为p的左子树
p.lchild = n.rchild
else:
p.rchild = n.rchild # 若n是p的右子树,则n的右子树变为p的右子树
elif n.rchild is None: # 若n的右子树为空
if n == p.lchild:
p.lchild = n.lchild
else:
p.rchild = n.lchild
else: # 若n的左右子树均不为空
pre = n.rchild
if pre.lchild is None: # 若n的右子树的左子树为空
n.data = pre.data # n右子树的数据赋给n
n.rchild = pre.rchild # n的右子树变为n的右子树的右子树
else: # 若n的右子树的左子树不为空
next = pre.lchild
while next.lchild is not None: # 一直向左遍历到左子树为空的节点
pre = next
next = next.lchild
n.data = next.data # 把左子树为空的节点的数据赋给n
pre.lchild = next.rchild # 该节点的右子树链到该节点的父节点的左子树
# 先序遍历
def preOrderTraverse(self, node):
if node is not None:
print(node.data)
self.preOrderTraverse(node.lchild)
self.preOrderTraverse(node.rchild)
# 中序遍历
def inOrderTraverse(self, node):
if node is not None:
self.inOrderTraverse(node.lchild)
print(node.data)
self.inOrderTraverse(node.rchild)
# 后序遍历
def postOrderTraverse(self, node):
if node is not None:
self.postOrderTraverse(node.lchild)
self.postOrderTraverse(node.rchild)
print(node.data)
a = [49, 38, 65, 97, 60, 76, 13, 27, 5, 1]
bst = BST(a) # 创建二叉查找树
print('遍历')
bst.inOrderTraverse(bst.root) # 中序遍历
print('删除元素')
bst.delete(bst.root, 49)
bst.inOrderTraverse(bst.root)
print('搜索')
res, node, parent = bst.search(bst.root, None, 97)
print(res, node.data, parent.data)
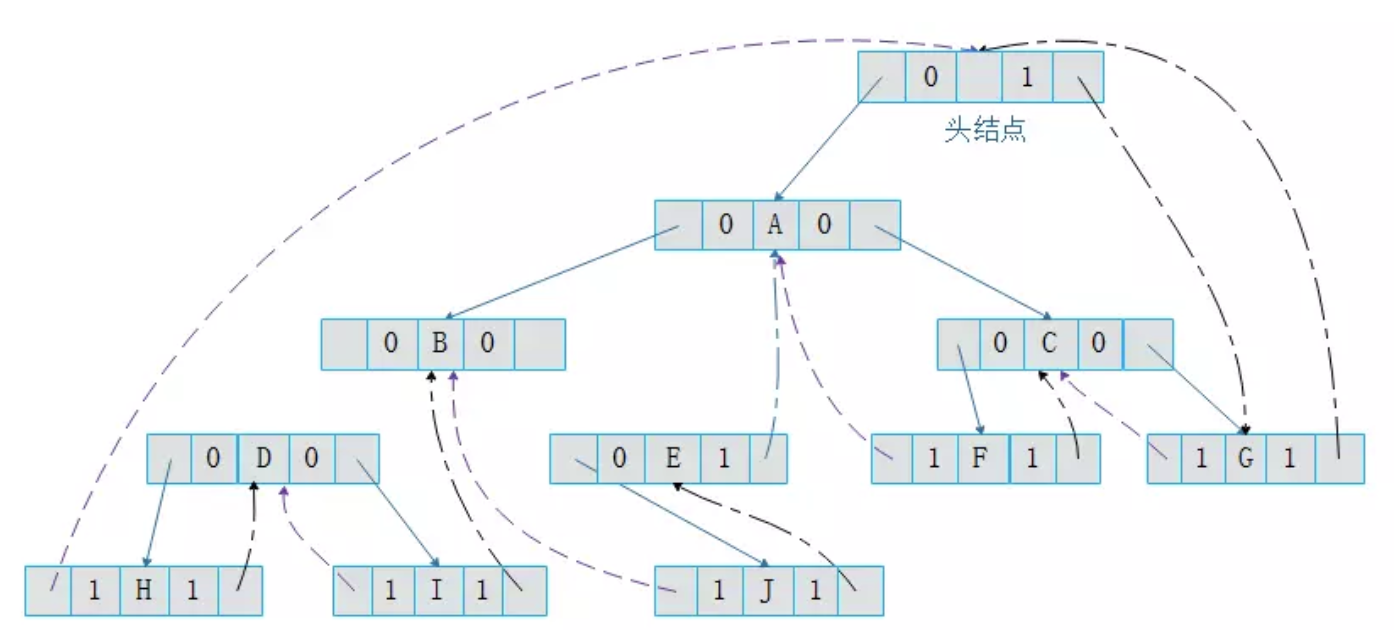
线索二叉树
对于n个节点的二叉树,采用二叉链表的形式存储,每个节点均有指向左右孩子的两个指针域,空指针就造成了空间浪费。

中序遍历得到的二叉树的中序序列包含着节点的前驱后继关系。如果在建立二叉树时就记录前驱后继的关系,那么在寻找前驱和后继节点时就不需要完成一次遍历。如何做?—— 将某节点的空指针域指向该点的前驱后继。若左子树为空,左孩子指针指向其前驱节点;若右孩子为空,右孩子指针指向其后继节点。
通过线索化,既解决了空间浪费问题,又解决了前驱后继记录问题。
但新问题:如何区分一个节点的左指针是指向其左孩子还是指向其中序遍历的前驱节点呢?——添加标志位ltag和rtag。ltag为0(Link)时指向该节点的左孩子,为1(Thread)时指向前驱;rtag为0时指向右孩子,为1时指向后继。
线索化的过程就是在中序遍历的过程中同时修改节点空指针的指向。为这个双向链表结构加上头节点,头节点左孩子指向原二叉树的根,右孩子指向中序遍历的最后一个节点。中序遍历第一个节点左指针指向头节点,最后一个节点右指针指向头节点。
树到二叉树的转换:1. 树中所有兄弟节点之间加一连线;2. 对每个节点只保留与其长子的连线;3. 调整位置。
二叉树到树的转换:1. 若节点x是双亲y的左孩子,则把x的右孩子,x右孩子的右孩子... 全部与y连起来;2. 去除所有双亲到右孩子的连线
森林到二叉树的转换:1. 将森林中的每棵树都转换为二叉树;2. 将各个二叉树的根依次连线;3. 调整位置。
二叉树到森林的转换:1. 若节点x是双亲y的左孩子,则把x的右孩子,x右孩子的右孩子... 全部与y连起来;2. 去除所有双亲到右孩子的连线;
二叉树的根节点有右孩子的话就是转换成森林,没有的话就是一棵树
树的遍历:先根遍历;后根遍历
森林的遍历:前序遍历;后序遍历(按照对应树的遍历方式遍历每一颗树)
树、森林的前根(序)遍历与其转换后的二叉树的前序遍历相同;后根(序)遍历与转换后的二叉树的中序遍历相同。
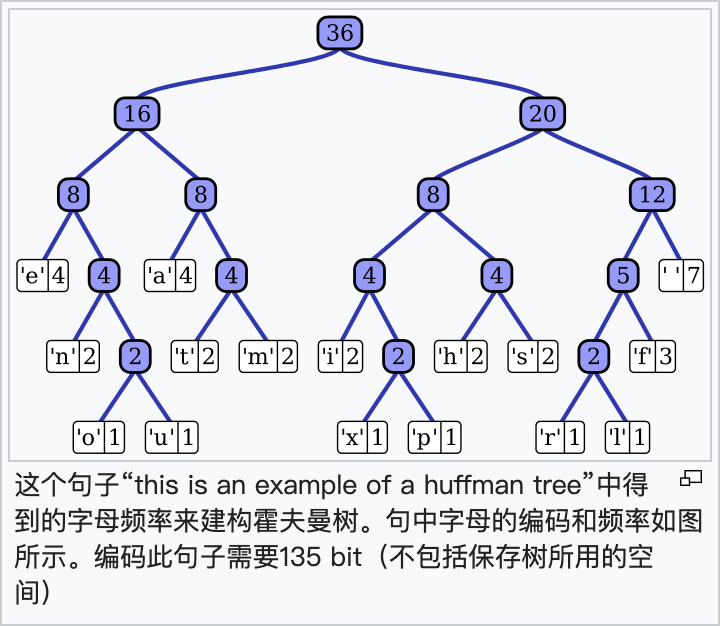
哈夫曼树
无损压缩算法。把二叉树简化为叶子结点带权的二叉树(树节点之间的连线相关的数叫做权weight)。某结点的路径长度为根节点到该节点的路径上的连接数。树的路径长度为叶子结点路径长度之和。带权路径长度:路径长度与节点权值的乘积。
哈夫曼树:树的带权路径长度最优的二叉树。
构造方法:
1. 森林中选出两颗根节点权值最小的二叉树;
2. 合并:增加一个新节点为根,权值为左右孩子(1中找出的两个二叉树)权值之和;
3. 从森林里再找一个二叉树的根节点,令其与新增节点为权值最小的两个。合并;
4. 一直这样做直到找到最后的根
哈夫曼编码
构造不等长的二进制编码,使编码后长度最短且无二义性。
定长编码(比如ASCII码)、变长编码(单个编码长度可根据整体出现频率来调节)、前缀码(没有任何码字是其他码字的前缀,比如哈夫曼编码)
哈夫曼编码:
1. 建立一个优先队列:按元素出现次数从小到大排一个队列
2. 构建一个哈夫曼树:队列前两个节点生成一个新节点,节点值就存放前两个权值之和,然后插回队列,前两个出队;最后队列就只剩一个元素,也就是这棵树的根节点
3.构建一个哈夫曼表:左子树都用0右子树都用1,遍历整棵树为每个叶子节点生成编码
4. 编码:根据哈夫曼表对给定的字符编码
5.解码:编码为0就往左边走一下,为1就往右边走一下... 最后实现解码

字典树 Trie

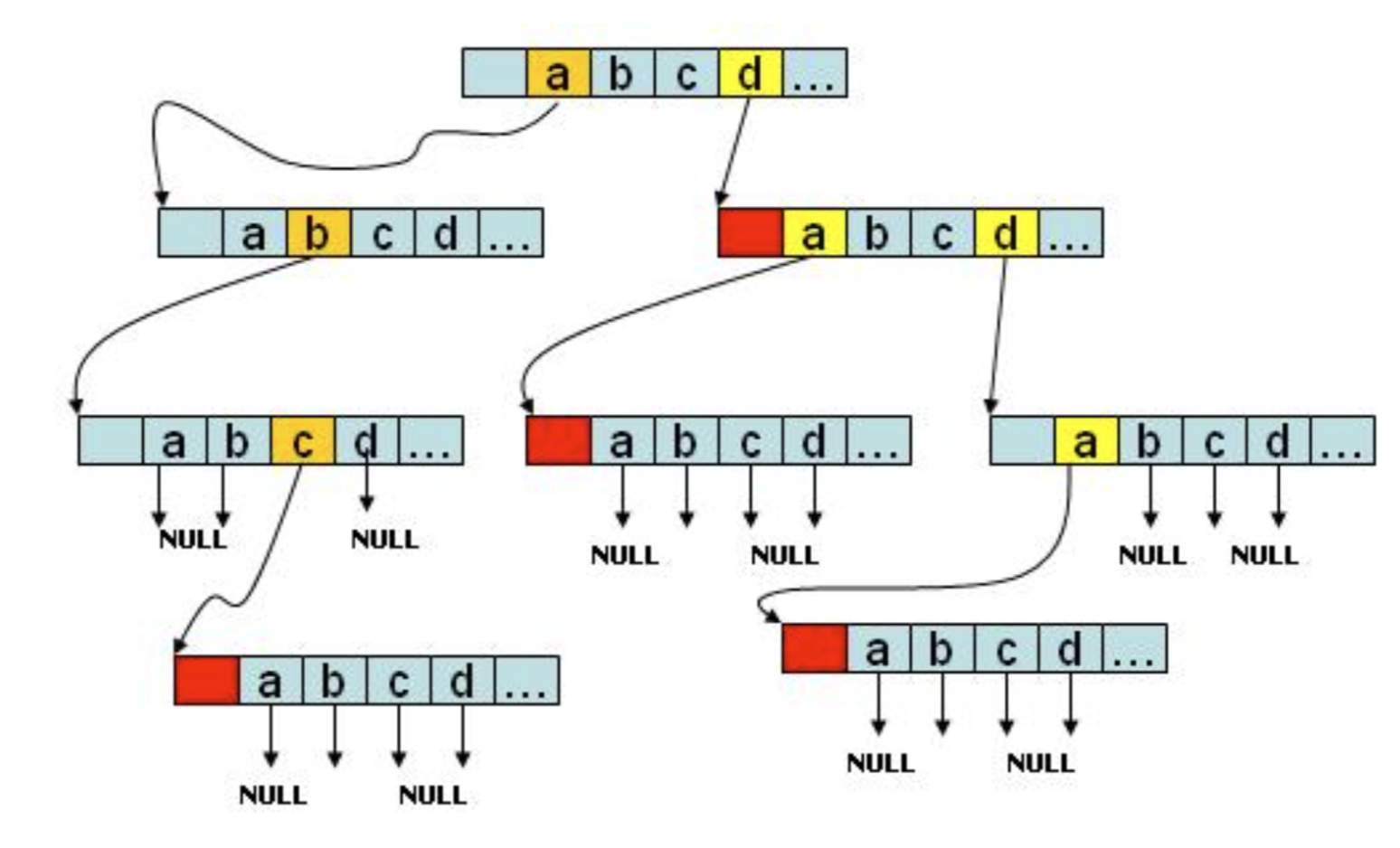
核心思想:空间换时间。利⽤字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
基本性质:
1. 根节点不包含字符,除根节点外每⼀个节点都只包含一个字符。
2. 从根节点到某⼀节点,路径上经过的字符连接起来,为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。
Leetcode #208 实现一个字典树。一级一级向下创建嵌套字典,比如上图分支to、tea,insert之后,root为{'t': {'o': {}, '#': {'#'}, 'e': {'a': {}, '#': {'#'} } } }
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = {} # 嵌套的字典
self.end_of_word = '#'
def insert(self, word: str) -> None:
"""
Inserts a word into the trie.
"""
node = self.root
for c in word: # 一级一级向下创建字典
node = node.setdefault(c, {}) # 如果root的键中没有c,就创建并赋值为{}
node[self.end_of_word] = self.end_of_word
def search(self, word: str) -> bool:
"""
Returns if the word is in the trie.
"""
node = self.root
for c in word:
if not c in node:
return False
node = node[c] # 一级一级向下,从字典中搜索字符是否存在
return self.end_of_word in node # 是否以'#'结尾
def startsWith(self, prefix: str) -> bool:
"""
Returns if there is any word in the trie that starts with the given prefix.
"""
node = self.root
for c in prefix:
if not c in node:
return False
node = node[c]
return True