面试题10:斐波那契数列
题目要求:
求斐波那契数列的第n项的值。f(0)=0, f(1)=1, f(n)=f(n-1)+f(n-2) n>1
思路:使用循环从下往上计算数列。
考点:考察对递归和循环的选择。使用递归的代码通常比循环简洁,但使用递归时要注意一下几点:1、函数调用的时间和空间消耗;2、递归中的重复计算;3、最严重的栈溢出。根据斐波那契数列递归形式定义很容易直接将代码写成递归,而这种方式有大量重复计算,效率很低。
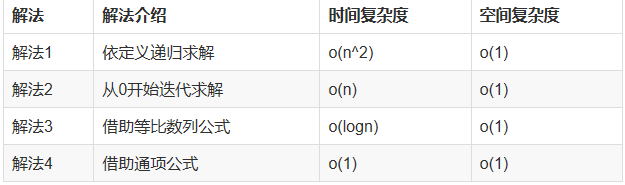
解法比较:
解法3,4将问题数学化,借助数学工具的推导,从根本上减低时间复杂度。
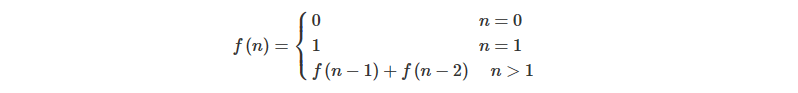
/** * Copyright(C) 2019 Hangzhou Differsoft Co., Ltd. All rights reserved. * */ package com.java.offer; /** * @since 2019年2月26日 下午12:59:43 * @author xuchao * * 斐波那契数列 f(0)=0,f(1)=1,f(n)=f(n-1)+f(n-2) n>1 */ public class P10_Fibonacci { // 1.依据原始概念的递归解法,时间复杂度o(n^2) public static int fibonacci1(int n) { if(n<=1) { return n; } return fibonacci1(n - 1) + fibonacci1(n - 2); } // 2.当前状态只与前两个状态有关。存储前两个值,计算后一个,迭代进行。时间复杂度o(n) public static int fibonacci2(int n) { if (n <= 1) { return n; } int f1 = 0; int f2 = 1; for (int i = 2; i <= n; i++) { int t = f1 + f2; f1 = f2; f2 = t; } return f2; } public static void main(String[] args) { System.out.println(fibonacci1(13)); System.out.println(fibonacci1(13)); } }