矩阵快速幂基本应用。
对于矩阵乘法与递推式之间的关系:
如:在斐波那契数列之中
f[i] = 1*f[i-1]+1*f[i-2] f[i-1] = 1*f[i-1] + 0*f[i-2]。即
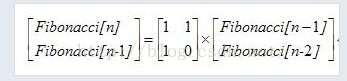
所以,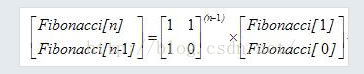
就这两幅图完美诠释了斐波那契数列如何用矩阵来实现。
1 #include<iostream> 2 #include<cstring> 3 using namespace std; 4 typedef long long ll; 5 const int Mod=10000; 6 struct mat{ 7 ll a[2][2]; 8 }; 9 mat mat_mul(mat x,mat y){ 10 mat ans; 11 memset(ans.a,0,sizeof(ans.a)); 12 for (int i=0;i<2;i++){ 13 for (int j=0;j<2;j++) 14 for (int k=0;k<2;k++) 15 ans.a[i][j]=ans.a[i][j]+(x.a[i][k]*y.a[k][j])%Mod; 16 } 17 return ans; 18 } 19 ll mat_pow(ll n){ 20 mat c,res; 21 c.a[0][0]=c.a[0][1]=c.a[1][0]=1; 22 c.a[1][1]=0; 23 memset(res.a,0,sizeof(res.a)); 24 for (int i=0;i<2;i++) res.a[i][i]=1; 25 while (n){ 26 if (n&1) res=mat_mul(res,c); 27 c=mat_mul(c,c); 28 n>>=1; 29 } 30 return res.a[0][1]%Mod; 31 } 32 int main(){ 33 ll n; 34 while (cin >> n && n!=-1){ 35 cout << mat_pow(n) << endl; 36 } 37 return 0; 38 }