背景:使用Logistic回归来预测患有疝气病的马的存活问题,这里的数据包括368个样本和28个特征,疝气病是描述马胃肠痛的术语,然而,这种病并不一定源自马的胃肠问题,其他问题也可能引发疝气病,该数据集中包含了医院检测马疝气病的一些指标,有的指标比较主观,有的指标难以测量,例如马的疼痛级别。另外,除了部分指标主观和难以测量之外,该数据还存在一个问题,数据集中有30%的值是缺失的。
1、准备数据:处理数据中的缺失值
数据中的缺失值是一个非常棘手的问题,那么数据缺失究竟带来了多少问题?假设有100个样本和20个特征,这些数据都是机器收集回来的,若机器上的某个传感器损坏导致一个特征无效时该怎么办?此时是否扔掉整个数据集?这种情况下,另外19个特征怎么办?它们是否还可用?答案是肯定的。因为有时数据相当昂贵,扔掉和重新获取都是不可取的,所以必须采用一些方法来解决这个问题。
下面给出了一些可选的做法:
(1)使用可用特征的均值来填补缺失值;
(2)使用特征值来填补缺失值,如-1;
(3)忽略有缺失值的样本;
(4)使用相似样本的均值填补缺少值;
(5)使用另外的机器学习算法预测缺失值。
现在我们要对下一节要用的数据集进行预处理,使其可以顺利地使用分类算法。在预处理阶段需要做两件事:(1)所有的缺失值必须用一个实数值来替换,因为我们使用的Numpy数据类型不允许包含缺失值,这里选择实数0来替换所有缺失值,恰好能适用于Logistic回归。另外,由于Sigmoid(0)=0.5,即它对结果的预测不具有任何的倾向性,因此上述做法不会对误差项造成任何影响。基于上述原因,将缺失值用0代替既可以保留现有数据,也不需要对优化算法进行修改。回归系数的更新公式如下:
weights=weights+alpha*error*dataMatrix[randIndex]
如果dataMatrix的某特征对应值为0,那么该特征的系数将不做更新,即:
weights=weights
(2)如果在测试数据集中发现一条数据的类别标签已经缺失,那么我们的简单做法是将该条数据丢弃。这是因为类别标签与特征不同,很难确定采用某个合适的值来替换。
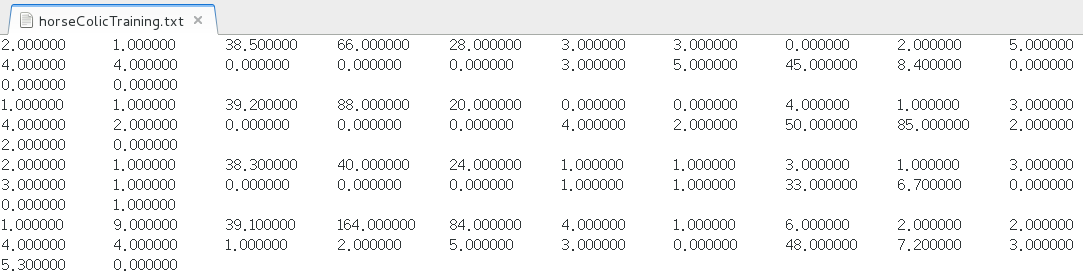
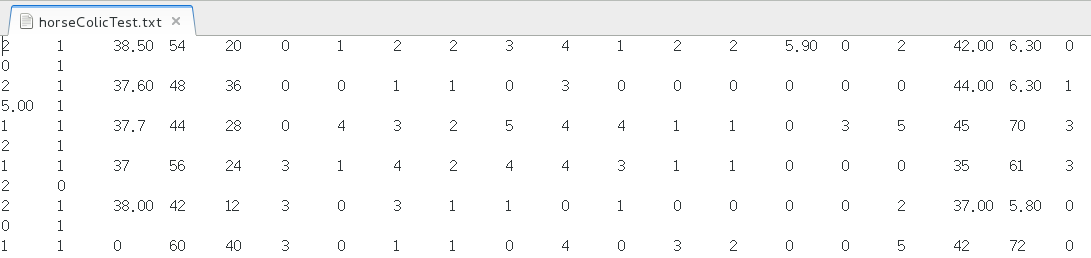
原始的数据经过预处理之后保存成两个文件:horseColicTest.txt和horseColicTraining.txt。如果想对原始数据和预处理后的数据做个比较,可以在http://archive.ics.uci.edu/ml/datasets/Horse+Colic浏览这些数据。
2、训练算法:改进的随机梯度上升算法
建立LogRegres.py文件,编写以下代码:
#改进的随机梯度上升函数
#!/usr/bin/python
# -*- coding: utf-8 -*-
from numpy import *
def sigmoid(inX):
return 1.0/(1+exp(-inX))
def stocGradAscent1(dataMatrix, classLabels, numIter=150): m,n = shape(dataMatrix) weights = ones(n) #initialize to all ones for j in range(numIter): dataIndex = range(m) for i in range(m): alpha = 4/(1.0+j+i)+0.01 #apha decreases with iteration, does not randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant h = sigmoid(sum(dataMatrix[randIndex]*weights)) error = classLabels[randIndex] - h weights = weights + alpha * error * dataMatrix[randIndex] del(dataIndex[randIndex]) return weights
3、测试算法:用Logistic回归进行分类
使用Logistic回归方法进行分类并不需要做很多工作,所需要做的只是把测试集上的每个特征向量乘以最优化方法得来的回归系数,再将该乘积结果求和,最后输入到Sigmoid函数中即可,如果对应的Sigmoid值大于0.5,就预测类别标签为1,否则为0。
下面看看实际运行效果,将下面代码添加到LogRegres.py文件中
#Logistic回归分类函数
def classifyVector(inX,weights): #判断分类
prob=sigmoid(sum(inX*weights))
if prob>0.5:
return 1.0
else:
return 0.0
def colicTest(): #导入数据
frTrain=open('horseColicTraining.txt')
frTest=open('horseColicTest.txt')
trainingSet=[];trainingLabels=[]
for line in frTrain.readlines():
currLine=line.strip().split(' ')
lineArr=[]
for i in range(21):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[21]))
trainWeights=stocGradAscent1(array(trainingSet),trainingLabels,500) #计算回归系数向量
errorCount=0;numTestVec=0.0
for line in frTest.readlines(): #导入测试集并计算分类错误率
numTestVec+=1.0
currLine=line.strip().split(' ')
lineArr=[]
for i in range(21):
lineArr.append(float(currLine[i]))
if int(classifyVector(array(lineArr),trainWeights))!=int(currLine[21]):
errorCount+=1
errorRate=(float(errorCount)/numTestVec)
print "the error rate of this test is: %f" %errorRate
return errorRate
def multiTest(): #调用函数colicTest()10次并求结果的平均值
numTests=10;errorSum=0.0
for k in range(numTests):
errorSum+=colicTest()
print "after %d iterations the average error rate is: %f" %(numTests,errorSum/float(numTests))
下面看一下实际的运行效果,在pyghon提示符下输入:
>>>import logRegres <module 'logRegres' from 'logRegres.py'> >>> logRegres.multiTest() the error rate of this test is: 0.343284 the error rate of this test is: 0.283582 the error rate of this test is: 0.432836 the error rate of this test is: 0.358209 the error rate of this test is: 0.328358 the error rate of this test is: 0.328358 the error rate of this test is: 0.343284 the error rate of this test is: 0.373134 the error rate of this test is: 0.432836 the error rate of this test is: 0.462687 after 10 iterations the average error rate is: 0.368657
从上面的结果可以看出,10次迭代之后的平均值错误率为37%,事实上,这个结果并不差,因为有30%的数据缺失。当然,如果调整colicTest()中的迭代次数和stocGradAscent1()中的步长,平均错误率可以降到20%左右。