二分算法:
hdu1969 PIE
题意:f+1个人分n分pie,pie只能切开不能从组,也就是说每个人拿到的必须是一个整块,不能是多个碎块。要求每个人分的的大小一样。n份pie的大小不同。目标是求出没人可能吃到的最大大小V。
分析抽象:首先条件是必须够n个人吃,要求大小一样的情况下求最大的V。关系是随着V的增大,所能support的人越少。这里有一个非递增的关系。所以而已考虑二分法。问题对精度的要求是二分法使用的关键。要求保留4位小数,所以我们统一乘上1000000来计算。
#include<iostream> #include<cstdio> #include<cmath> #define PI acos(long double(-1)) using namespace std; long long a[10000+1]; long long low, high, mid, res; int N, F; bool judge() { int num = 0; for(int i =0; i<N; i++) { num += a[i]/mid; } return num>=F+1; } int main() { int T; long long t; int i; cin>>T; while(T-->0) { cin>>N>>F; long long max = 0; for(i=0; i<N; i++) { cin>>t; a[i] = t*t*PI*1000000; if(a[i]>max) max = a[i]; } low = 0; high = max; while(low<=high) { mid = (high + low)/2; if(judge()) { low = mid+1; res = mid; } else high = mid-1; } printf("%.4lf ",(double)res/1000000); } return 0; }
总结:二分法竟然还可以这样使用,看来对于单调的关系,求满足某种关系的特定值问题都可以考虑二分法。
关于这个问题还有讨论点:
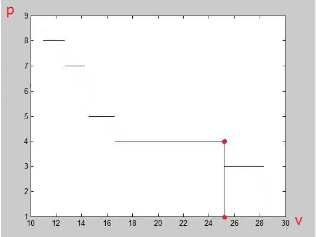
这是针对第一组测试数据画的图,图中的红点即为要求值。但是如果改变题目的意思,要求p=4时所对应的最小值,该怎么办呢。
其实这个问题就变成了二分搜索中求第一个目标值和最后一个目标值的问题了。
举例:6 7 8 8 8 9 10 这7个数的存在a[]中,分别写出求第一个8和最后一个8的算法代码;
求第一个:
1 l = 0, r = 6; 2 while(l<r) 3 { 4 mid = (l + r)/2; 5 if(a[mid]>=8) 6 r = mid - 1; 7 else 8 l = mid + 1; 9 } 10 ans = l;
求最后一个:
l = 0, r = 6; while(l<r) { mid = (l + r)/2; if(a[mid]<=8) l = mid + 1; else r = mid - 1; } ans = r;
本题选用的是后者。
可见实际问题只要抽象成数学问题分析起来就单纯的多了。
POJ-3273
题意:FJ已知未来N天的每天花费细节,现在他要把这N天分成M个连续的时间段,求M段中最小的花费。
sample:7天5份 7天的花费分别是 100 400 300 100 500 101 400; 这个结果是500。
在这里简单分析一下:网上的大神们都说看到这个题目首想的是DP(其实不可行),但做为一个小菜鸟对DP理解有限,还不能理解到此题和DP有什么关系。
既然用二分法就要首先确定单调的关系,目标是求出最大花费段—v。那么显然v越大,一贪心的思想来看(就是每个连续段再加上下一天的花费就会超过v)所能划分的段数就会越少,单调关系确定,下面来确定v的上下界,l显然是max{每天的花费},r是sum{每天的花费}。l<=v<=r。这就可以了,下面是AC的代码:(补充一句:这个题属于我上面总结的第二种情况)
1 #include<stdio.h> 2 #include<iostream> 3 4 using namespace std; 5 6 int N,M,l,r,mid; 7 int a[1000000+2]; 8 9 bool judge() 10 { 11 int num = 0; 12 int s = 0; 13 for(int i =0 ;i<N;i++) //这里要考虑到最后一段所以在if语句中加上了++num, 14 { 15 s+=a[i]; 16 if(s>mid) 17 { 18 num++; 19 s = a[i]; 20 } 21 } 22 if(++num>M) //这里的判断为什么不是>=呢? 23 return true; 24 else 25 return false; 26 } 27 28 int main() 29 { 30 cin>>N>>M; 31 int sum = 0; 32 int max = 0; 33 for(int i =0; i<N;i++) 34 { 35 cin>>a[i]; 36 if(max<a[i]) 37 max = a[i]; 38 sum+=a[i]; 39 } 40 r = sum; 41 l = max; 42 mid; 43 while(l<r) 44 { 45 mid = (l + r)/2; 46 if(judge()) 47 { 48 l = mid+1; 49 } 50 else 51 r = mid -1; 52 } 53 cout<<r<<endl; 54 return 0; 55 }
在交代码的时候遇到了一个问题,看来要好好在研究一下细节了。
judge函数中我本来写的是if(++num>=M)但得到是WA,改后才是AC。
先歇会儿,待会再研究!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
三分算法: