动态规划算法的核心
//动态规划算法的核心就是记住已经解决过的子问题的解
通过动态规划解决斐波那契数列
//斐波那契数列(Fibonacci) //递归法 int fib(int n) { if (n == 0) return 0; if (n == 1) return 1; return fib(n-1) + fib(n-2);//n=6 ,返回8 }
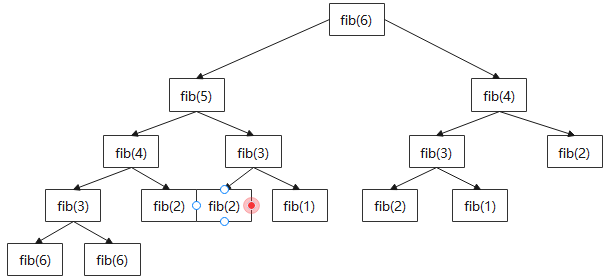
//执行流程,可以看出递归,很多重复的节点被执行,其中fib(2)被重复执行5次。 //由于调用每一个函数都要保留上下文,所以空间开销不小。 //通过备忘录把被执行过的子节点保存起来,后边在调用直接使用,节约大量时间。
动态规划算法的两种形式
//1. 自顶向下的备忘录法 //2. 自底向上
自顶向下的备忘录法
#include <iostream> using namespace std; int fib(int n, int memo[]) { if (memo[n] != -1) return memo[n];//递归发现fib(n)已经算出来则保存并返回 if (n <= 2) memo[n] = 1; else memo[n] = fib(n-1,memo) + fib(n-2,memo); return memo[n]; } int main() { int n,sum=0; scanf("%d",&n);//6 if (n == 0) sum = 0; else { int memo[n+1];//创建备忘录保存求出的斐波拉契数列中的每一个值 for (int i=0; i<=n; i++) memo[i] = -1;//初始化 sum = fib(n,memo);//调用斐波那契数列函数 } printf("%d ",sum);//8 return 0; }
自底向上的动态规划
//自底向上方法也是利用数组保存了先计算的值,为后面的调用服务 int fib(int n) { if (n==0) return n; int memo[n+1]; memo[0] = 0; memo[1] = 1; for (int i=2; i<=n; i++) memo[i] = memo[i-1] + memo[i-2]; return memo[n]; } //或者进一步压缩空间 #include <iostream> using namespace std; int fib(int n) { if (n==0) return n; int memo1 = 0; int memo2 = 1; int memo3 = 1; for (int i=2; i<=n; i++) { memo3 = memo1 + memo2;//最终的和 memo1 = memo2;//第二项赋值给第一项 memo2 = memo3;//第三项赋值给第二项 } return memo3; } int main() { int n; scanf("%d",&n);//6 cout << fib(n); return 0; }
动态规划的使用
//1. 最优子结构 //如果一个问题的解结构包含其子问题的最优解,就称此问题具有最优子结构性质 //使用动态规划算法时,用子问题的最优解来构造原问题的最优解。 //2. 重叠子问题 //如果递归算法反复求解相同的子问题,就称为具有重叠子问题(overlapping subproblems)性质。 //在动态规划算法中使用数组来保存子问题的解,这样子问题多次求解的时候可以直接查表不用调用函数递归。
原文链接:https://blog.csdn.net/u013309870/article/details/75193592