该章节涉及到知识图谱的知识,我们先说几个概念
1.节点和边
节点就是现实世界存在的实体,边就是实体和实体之间的关系
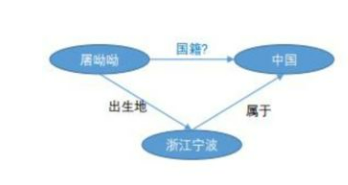
2.权重
权重通常用与衡量关系的强弱,权重越大,比如说用户A给用户B打了15个电话,则权重为15
3.有向图无向图
根据边是否有方向,分为有向图和无向图,比如说用户A给用户B打了15个电话就是有向图,但是A和B是同事就是无向图了。
4.中心度和相似性
中心度来衡量网络中每一个节点的活跃程度,其中衡量中心度有多重方式,下面介绍几种表示方法
(1)度:节点的度是指与该节点相连的边的个数,节点的度越大,说明该节点在该网络中越活跃,使groupby和count或者nunique()结合使用可以计算度,也可以使用networkx.degree()计算
(2)Eigenvector中心度:只是使用度就是中心度,乜有考虑到邻接节点的信息,Eigenvector的设计思想是一个节点的活跃并不只体现他有非常大的度,还体现与他相连的节点也有非常多的度。
(3)Pagerank
(4)Bbtweennss
Jaccard相似度
5.节点分类
要对节点进行分类预测,首先要找到从网络中抽取特征的方法,即通过特殊的表达手段,将网络中的节点空间关系抽象为一个向量
(1)朴素节点分类
朴素节点分类思想非常简单,只需要根据节点与其他节点是否相连,进行one-hot编码后,排列成列向量,和标签一起带人分类器进行训练
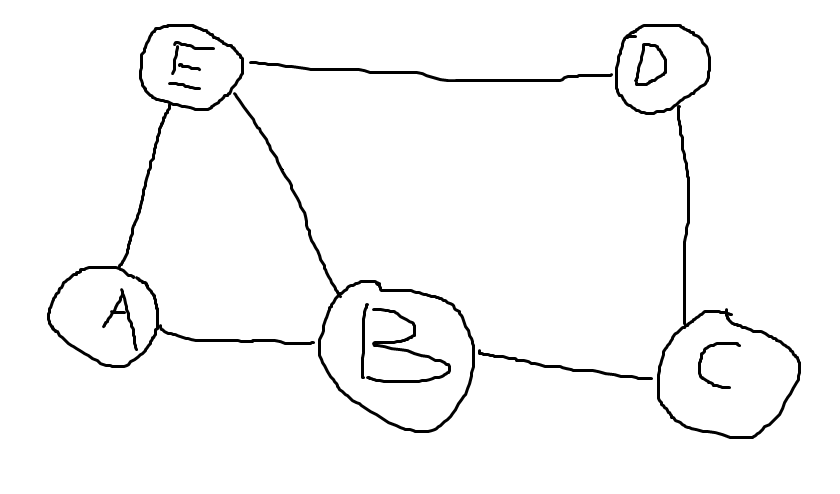
节点A的向量 表示为[0,1,0,0,1]
因为A和B、E向量,因此[A,B,C,D,E]只有B和E的位置是1,其余都是0
(2)邻节点加权投票
在知识图谱中,通常认为,用户 的信息会由边进行传播并不断衰减,而朴素节点分类中,没有考虑到节点之间的相互作用,一般来说相连的用户可能具有相同的标签,比如一个用户被打上欺诈标签,那么他的一度联系人会转变成欺诈用户的概率会大大提高,这种情况下,可以使用一种叫共生节点分类的半监督学习方法对节点进行分类。
邻节点加权投票(WVRN)是一种典型的共生节点分类法,每一个无标签节点 i 的标签由其邻居 N(i)进行加权投票得到,公式到时再补上
权重就体现在节点 i 的邻居节点标签的概率上,也就是说,邻居中对自己标签最有信息的节点,对应节点 i 的贡献也会越大,从而可以根据网络中部分有标签样本的标签,迭代得到其余无标签样本的标签,最终,网络中的每个节点的标签概率会收敛到一个稳定的值。
(3)一致性标签传播
根据邻居节点概率加权投票的方式,虽然考虑到了节点信息的流转,但是每一次更新的时候都没有将自身的信息考虑进去,简单来说,一个节点在经历一次更新时,相比自身原来的标签不应该有太大的改变。如果想把每个节点自身的信息考虑进去,可以使用另一种共生节点分类的算法,一致性标签传播(CLPM),一致性标签传播也是一种半监督的学习方法,可以根据网络中有部分标签样本的标签,迭代得到其余无标签的样本的标签。
6.社区发现算法
对于团伙欺诈检测,主要有2类发现算法:
(1)社区检测:通过对固定的网络社区进行划分,从而得到一个个团簇结构;
(2)社区搜索:首先给定一个网络社区和其中的某个节点A,然后从节点A出发寻找与A有关的社区;
GN算法:Girvan-Newman算法是最经典的社区发现算法之一,基本思想是,如果去除社群之间连接的边,留下的就是社群。该算法认为,2个社群之间的点的最短路径总是要通过社群间的连接边,因此中心度越大的边,越可能是不同社群的连接边,所以只需要不断将中心度大的边去掉,就可以得到独立的社群。
算法步骤如下:
(1)计算所有边的边中心度;
(2)将边中心度最高的边去掉;
(3)重新计算被去掉的边影响的边的边中心度;
(4)重新第2和第3步,直至不连通的社群个数达到预想值;
import networkx as nx from networkx.algorithms import community import itertools G = nx.karate_club_graph() nx.draw(G,with_labels=True, edge_color='grey', node_color='pink', node_size = 500, font_size = 40, pos=nx.spring_layout(G,k=0.2)) comp = community.girvan_newman(G) # 令社区个数为4,这样会依次得到K=2,K=3,K=4时候的划分结果 k = 4 limited = itertools.takewhile(lambda c: len(c) <= k, comp) for communities in limited: print(tuple(sorted(c) for c in communities))
Louvain算法
在实际使用中,GN算法虽然准确率很高,但是计算量很大,时间复杂度也高,因此再推出Louvain算法