kaggle 2015年航班延误

数据来源：https://www.kaggle.com/usdot/flight-delays

该数据集完整数据量有500多万条航班记录数据，特征有31个

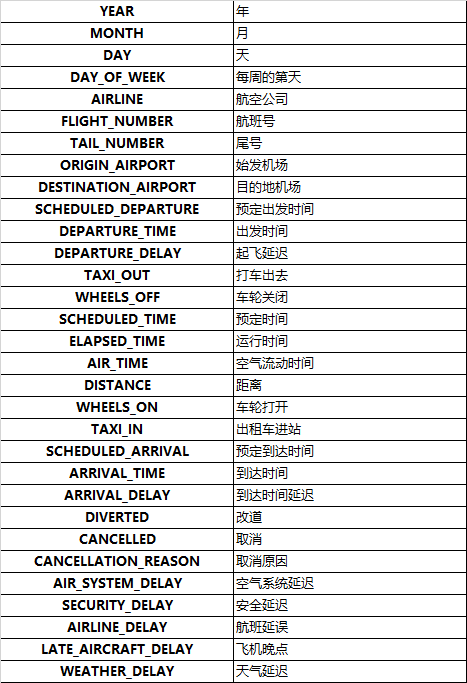
 感觉这个数据不是很好，如果我们将ARRIVAL_DELAY作为y值，但是后面的空气系统延误，安全延误感觉又像是延误的原因，我们首先看一下数据怎么样

1.由于数据量实在是太多，我们抽取其中一些数据

#%%导入模块
import pandas as pd 
import numpy as np
from scipy import stats
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
plt.rc("font",family="SimHei",size="12")  #解决中文无法显示的问题
import pycard as pc


#%%导入数据
#%% 读取flights数据集
flights = pd.read_csv('D:/迅雷下载/flights.csv')
# 数据集抽样1%
flights = flights.sample(frac=0.01, random_state=10)
flights.shape  #(58191, 31)

2.将ARRIVAL_DELAY超过10min作为延误

flights["y"] = (flights["ARRIVAL_DELAY"]>10)*1
flights.pop("ARRIVAL_DELAY")

3.区分类别型变量和数值型变量

cate_col = flights.select_dtypes(include='object').columns.to_list()
num_col = [i for i in flights.columns if i not in cate_col]

4.计算数值型变量的iv值

#%%数值变量的iv值计算
num_iv_woedf = pc.WoeDf()
clf = pc.NumBin() #min_bin_samples=20, min_impurity_decrease=4e-5
for i in num_col:
    clf.fit(flights[i] ,flights.y)
    #clf.generate_transform_fun()
    num_iv_woedf.append(clf.woe_df_)
num_iv_woedf.to_excel('tmp1')

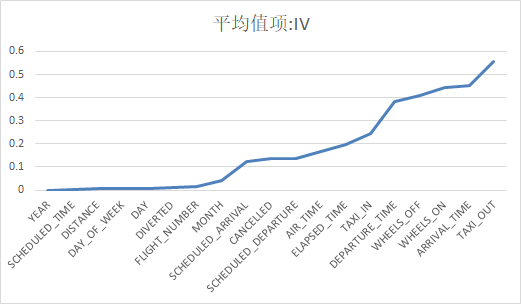
 剩下的几个值太大了

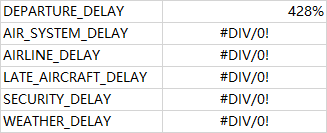
 再仔细看看后面这5个

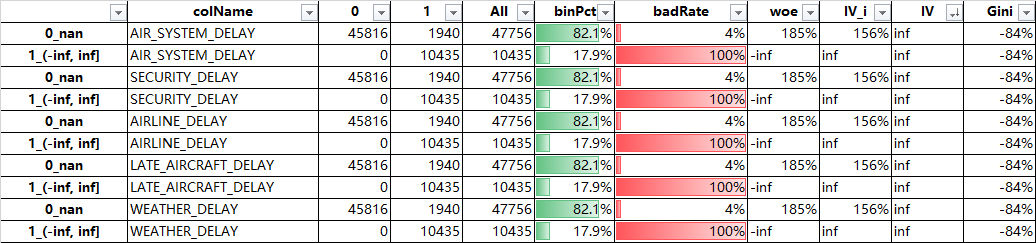
 这几个变量其实也是延误的原因，我们不可以那它作为特征，（如果不了解字段原因，遇到这个等于无穷的情况，我们可以将这些变量作为特征，但是这次的明显不是特征，我们把这些变量删除掉）

5.类别型变量

#类别型变量
cate_iv_woedf = pc.WoeDf()
for i in cate_col:
    cate_iv_woedf.append(pc.cross_woe(flights[i] ,flights.y))
cate_iv_woedf.to_excel('tmp2')

类别型变量的类别太多了，暂时不使用这些变量

6.中间的一些处理

这步是去掉iv值比较低的变量

drop_num = ["MONTH",
"FLIGHT_NUMBER",
"DIVERTED",
"DAY",
"DAY_OF_WEEK",l
"DISTANCE",
"SCHEDULED_TIME",
"YEAR"]

# 去掉这些
num_col = [i for i in num_col if i not in drop_num]
num_iv_woedf = pc.WoeDf()
clf = pc.NumBin() #min_bin_samples=20, min_impurity_decrease=4e-5
for i in num_col:
    clf.fit(flights[i] ,flights.y)
    #flights[i+'_bin'] = clf.transform(flights[i])  #这样可以省略掉后面转换成_bin的一步骤
    num_iv_woedf.append(clf.woe_df_)

相关性处理

flights[num_col].corr().to_excel('tmp2.xlsx')

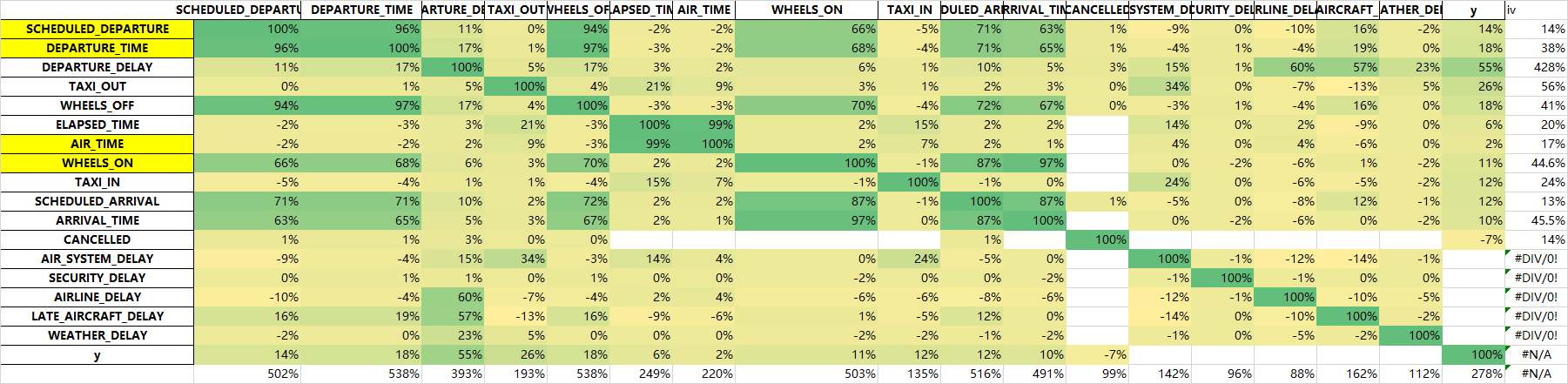
 再删除上面说的延误原因的那五个字段

7.最后入模字段

num_col = ["DEPARTURE_DELAY",
"TAXI_OUT",
"WHEELS_OFF",
"ELAPSED_TIME",
"TAXI_IN",
"SCHEDULED_ARRIVAL",
"ARRIVAL_TIME",
"CANCELLED"]
num_iv_woedf = pc.WoeDf()
clf = pc.NumBin() #min_bin_samples=20, min_impurity_decrease=4e-5
for i in num_col:
    clf.fit(flights[i] ,flights.y)
    flights[i+'_bin'] = clf.transform(flights[i])  #这样可以省略掉后面转换成_bin的一步骤
    num_iv_woedf.append(clf.woe_df_)
    

 

 

 

 

 

 

 

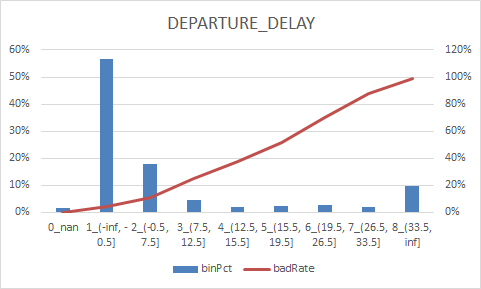
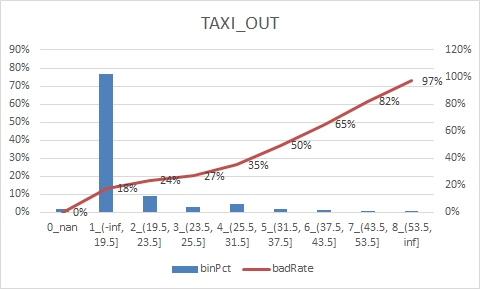
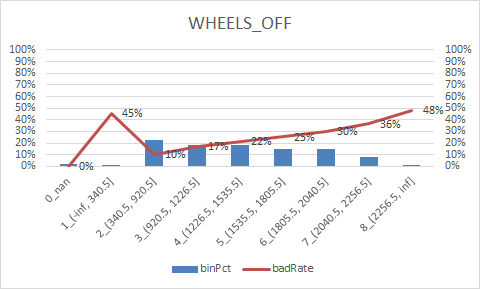
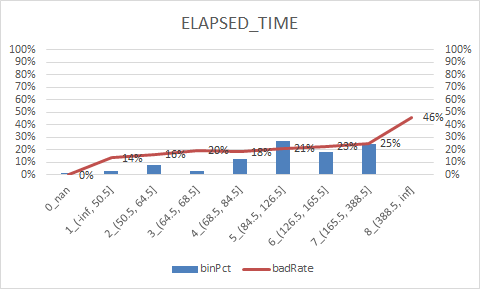
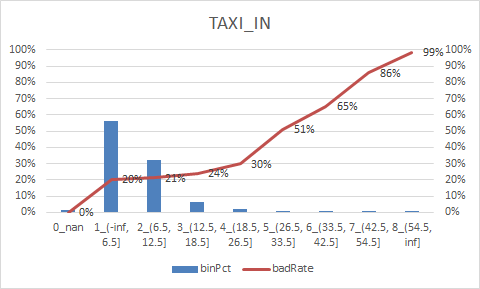
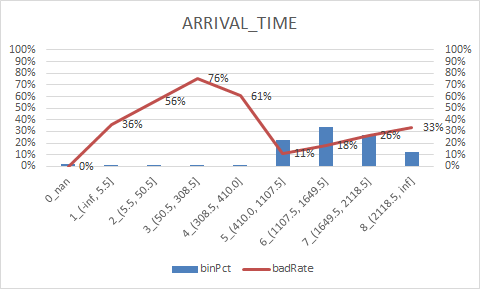
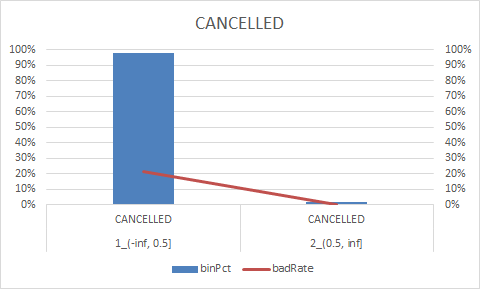
 8.woe转换

#%%woe转换
bin_col = [i for i in list(flights.columns) if i[-4:]=='_bin']

cate_iv_woedf = pc.WoeDf()
for i in bin_col:
    cate_iv_woedf.append(pc.cross_woe(flights[i] ,flights.y))
#cate_iv_woedf.to_excel('tmp1')
cate_iv_woedf.bin2woe(flights,bin_col)

9.建模

model_col = [i for i in list(flights.columns) if i[-4:]=='_woe']

import pandas as pd
import matplotlib.pyplot as plt #导入图像库
import matplotlib
import seaborn as sns
import statsmodels.api as sm
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split

X = flights[model_col]
Y = flights['y']


x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.25,random_state=100)


X1=sm.add_constant(x_train)   #在X前加上一列常数1，方便做带截距项的回归
logit=sm.Logit(y_train.astype(float),X1.astype(float))
result=logit.fit()
result.summary()
result.params

10.训练集效果

resu_1 = result.predict(X1.astype(float))
fpr, tpr, threshold = roc_curve(y_train, resu_1)
rocauc = auc(fpr, tpr)  #0.9599064590567914
plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % rocauc)
plt.legend(loc='lower right')
plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('真正率')
plt.xlabel('假正率')
plt.show()

# 此处我们看一下混淆矩阵
from sklearn.metrics import precision_score, recall_score, f1_score,confusion_matrix
#lr = LogisticRegression(C=best_c, penalty='l1')
#lr.fit(X_train_undersample, y_train_undersample)
#y_pred_undersample = lr.predict(X_train_undersample)

resu_1 = resu_1.apply(lambda x :1 if x>=0.5 else 0)
matrix = confusion_matrix(y_train, resu_1)
print("混淆矩阵:
", matrix)
print("精度:", precision_score(y_train, resu_1))
print("召回率:", recall_score(y_train, resu_1))
print("f1分数:", f1_score(y_train, resu_1))
'''
混淆矩阵:
 [[33506   866]
 [ 2305  6966]]
精度: 0.8894279877425945
召回率: 0.7513752561751699
f1分数: 0.8145939308893178
'''

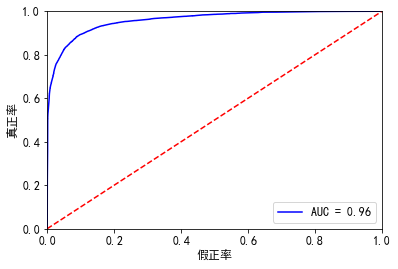
 11.测试集效果

#%%验证集
X3 = sm.add_constant(x_test)
resu = result.predict(X3.astype(float))
fpr, tpr, threshold = roc_curve(y_test, resu)
rocauc = auc(fpr, tpr)  #0.9618011576768271
plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % rocauc)
plt.legend(loc='lower right')
plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('真正率')
plt.xlabel('假正率')
plt.show()

# 此处我们看一下混淆矩阵
from sklearn.metrics import precision_score, recall_score, f1_score,confusion_matrix
#lr = LogisticRegression(C=best_c, penalty='l1')
#lr.fit(X_train_undersample, y_train_undersample)
#y_pred_undersample = lr.predict(X_train_undersample)

resu = resu.apply(lambda x :1 if x>=0.5 else 0)
matrix = confusion_matrix(y_test, resu)
print("混淆矩阵:
", matrix)
print("精度:", precision_score(y_test, resu))
print("召回率:", recall_score(y_test, resu))
print("f1分数:", f1_score(y_test, resu))
'''
混淆矩阵:
 [[11168   276]
 [  740  2364]]
精度: 0.8954545454545455
召回率: 0.7615979381443299
f1分数: 0.8231197771587743
'''

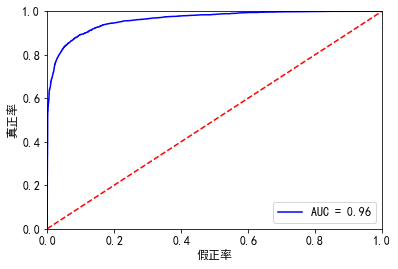
 总结：

由于数据的原因，该数据不是很典型，只适合练练手，所以后面的我就不深究