一、kmeans概述
K-means聚类算法也称k均值聚类算法,属于无监督学习的一种,k-means聚类无需给定Y变量,只有特征X。
K-means聚类算法是一种迭代求解的聚类分析算法,其步骤是随机选取K个对象作为初始的聚类中心,然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本,聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类,没有(或最小数目)聚类中心再发生变化,误差平方和局部最小
具体算法描述如下:
1、 随机选取k个聚类质心点(cluster centroids)为。
2、 重复下面过程直到收敛 {
对于每一个样例i,计算其应该属于的类
对于每一个类j,重新计算该类的质心
K是我们事先给定的聚类数,代表样例i与k个类中距离最近的那个类,
的值是1到k中的一个。质心
代表我们对属于同一个类的样本中心点的猜测,拿星团模型来解释就是要将所有的星星聚成k个星团,首先随机选取k个宇宙中的点(或者k个星星)作为k个星团的质心,然后第一步对于每一个星星计算其到k个质心中每一个的距离,然后选取距离最近的那个星团作为
,这样经过第一步每一个星星都有了所属的星团;第二步对于每一个星团,重新计算它的质心
(对里面所有的星星坐标求平均)。重复迭代第一步和第二步直到质心不变或者变化很小。
K-means面对的第一个问题是如何保证收敛,前面的算法中强调结束条件就是收敛,可以证明的是K-means完全可以保证收敛性。下面我们定性的描述一下收敛性,我们定义畸变函数(distortion function)如下:
J函数表示每个样本点到其质心的距离平方和。K-means是要将J调整到最小。假设当前J没有达到最小值,那么首先可以固定每个类的质心,调整每个样例的所属的类别
来让J函数减少,同样,固定
,调整每个类的质心
也可以使J减小。这两个过程就是内循环中使J单调递减的过程。当J递减到最小时,
和c也同时收敛。(在理论上,可以有多组不同的
和c值能够使得J取得最小值,但这种现象实际上很少见)。
由于畸变函数J是非凸函数,意味着我们不能保证取得的最小值是全局最小值,也就是说k-means对质心初始位置的选取比较感冒,但一般情况下k-means达到的局部最优已经满足需求。但如果你怕陷入局部最优,那么可以选取不同的初始值跑多遍k-means,然后取其中最小的J对应的和c输出
二、kmeans的损失函数
和其他机器学习算法一样,K-Means 也要评估并且最小化聚类代价,在引入 K-Means 的代价函数之前,先引入如下定义:

引入代价函数:
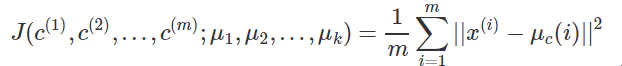
三、kmeans的优缺点
优点:
1)原理比较简单,实现也是很容易,收敛速度快。
2)聚类效果较优。
3)算法的可解释度比较强。
4)主要需要调参的参数仅仅是簇数k。
缺点:
1)K值的选取不好把握
2)对于不是凸的数据集比较难收敛
3)如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果不佳。
4) 采用迭代方法,得到的结果只是局部最优。
四、kmeans参数
class sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init=10, max_iter=300, tol=0.0001,
precompute_distances='deprecated', verbose=0, random_state=None, copy_x=True, n_jobs='deprecated', algorithm='auto')
- n_clusters:int, default=8,簇的个数,即你想聚成几类
- init:{'k-means++', 'random', ndarray, callable}, default=’k-means++’,初始簇中心的获取方法,'k-means ++':以一种聪明的方式为k-mean聚类选择初始聚类中心,以加快收敛速度。有关更多详细信息,请参见k_init中的注释部分。'random':n_clusters从初始质心的数据中随机选择观察(行)。如果传递了ndarray,则其形状应为(n_clusters,n_features),并给出初始中心。如果传递了callable,则应使用参数X,n_clusters和随机状态并返回初始化
- n_init:int, default=10,获取初始簇中心的更迭次数,k均值算法将在不同质心种子下运行的次数
- max_iter:int, default=300,最大迭代次数(因为kmeans算法的实现需要迭代),单次运行的k均值算法的最大迭代次数
- tol:float, default=1e-4,容忍度,即kmeans运行准则收敛的条件,关于Frobenius范数的相对容差,该范数表示两个连续迭代的聚类中心的差异,以声明收敛
- precompute_distances:{'auto', True, False}, default='auto',是否需要提前计算距离,这个参数会在空间和时间之间做权衡,如果是True 会把整个距离矩阵都放到内存中,auto 会默认在数据样本大于featurs*samples 的数量大于12e6 的时候False,False 时核心实现的方法是利用Cpython 来实现的
- verbose:int, default=0,冗长模式(不太懂是啥意思,反正一般不去改默认值)
- random_state:int, RandomState instance, default=None,确定质心初始化的随机数生成。使用整数使随机性具有确定性
- copy_x:bool, default=True, 对是否修改数据的一个标记,如果True,即复制了就不会修改数据。bool 在scikit-learn 很多接口中都会有这个参数的,就是是否对输入数据继续copy 操作,以便不修改用户的输入数据。这个要理解Python 的内存机制才会比较清楚
- n_job:sint, default=None,并行设置
- algorithm:{'auto', 'full', 'elkan'}, default='auto',kmeans的实现算法,经典的EM风格算法是'full'的。通过使用三角形不等式,'elkan'变异对于定义良好的聚类的数据更有效。但是,由于分配了额外的形状数组(n_samples,n_clusters),因此需要更多的内存。目前,'auto'(保持向后兼容性)选择'elkan',但为了更好的启发式,将来可能会更改
属性
- cluster_centers_:ndarray(n_clusters, n_features),集群中心的坐标
- labels_:ndarray(n_samples,),每个点的标签
- inertia_:float,样本到其最近的聚类中心的平方距离的总和
- n_iter_:int,运行的迭代次数
方法
- fit(X[, y, sample_weight]):拟合,计算k均值聚类
- fit_predict(X[, y, sample_weight]):计算聚类中心并预测每个样本的聚类索引
- fit_transform(X[, y, sample_weight]):计算聚类并将X转换为聚类距离空间
- get_params([deep]):获取此估计量的参数
- predict(X[, sample_weight]):预测X中每个样本所属的最近簇
- score(X[, y, sample_weight]):与K均值目标上X的值相反
- set_params(**params):设置此估算器的参数
- transform(X):将X转换为群集距离空间
也可以看看MiniBatchKMeans
替代性在线实施,使用微型批次对中心位置进行增量更新。对于大规模学习(例如n_samples> 10k),MiniBatchKMeans可能比默认的批处理实现要快得多。
sklearn.cluster.k_means
sklearn.cluster.k_means(X, n_clusters, *, sample_weight=None, init='k-means++', precompute_distances='deprecated', n_init=10,
max_iter=300, verbose=False, tol=0.0001, random_state=None, copy_x=True, n_jobs='deprecated', algorithm='auto', return_n_iter=False)
- X:{array-like, sparse} matrix of shape (n_samples, n_features),数组,矩阵,稀疏矩阵
- n_clusters:int
- sample_weight:array-like of shape (n_samples,), default=None,X中每个观测值的权重。如果为None,则为所有观测值分配相等的权重
- init:{'k-means++', 'random', ndarray, callable}, default='k-means++'
- precompute_distances:{'auto', True, False}
- n_init:int, default=10
- max_iter:int, default=300
- verbose:bool, default=False
- tol:float, default=1e-4
- random_state:int, RandomState instance, default=None
- copy_x:bool, default=True
- n_jobs:int, default=None
- algorithm:{'auto', 'full', 'elkan'}, default='auto'
- return_n_iter:bool, default=False
属性
- centroid
- label
- inertia
- best_n_iter
k_means这个是先写的,他们两的参数就相差一个数据集,不过还是建议用KMeans
五、kmeans可视化
使用iris数据做简单的聚类,并且画出聚类后的图片
import numpy as np import matplotlib.pyplot as plt import pandas as pd from sklearn.datasets import load_iris from sklearn.cluster import KMeans X=load_iris().data kmeans = KMeans(n_clusters=3,random_state=0) kmeans.fit(X) labels = kmeans.labels_ labels = pd.DataFrame(labels,columns=['labels']) X=pd.DataFrame(X) X.insert(4,'labels',labels) from sklearn.manifold import TSNE tsne = TSNE() a = tsne.fit_transform(X) liris = pd.DataFrame(a,index=X.index) d1 = liris[X['labels']==0] #plt.plot(d1[0],d1[1],'r.') d2 = liris[X['labels']==1] #plt.plot(d2[0],d2[1],'go') d3 = liris[X['labels']==2] #plt.plot(d3[0],d3[1],'b*') plt.plot(d1[0],d1[1],'r.',d2[0],d2[1],'go',d3[0],d3[1],'b*')

值得注意的是,上面的可视化是将特征缩成一个值,然后在和label画图
还有其他的可视化方法
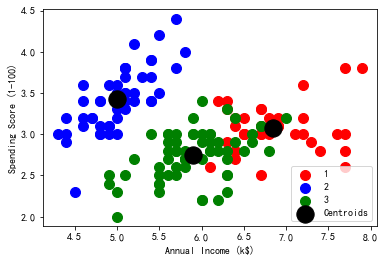
# 导入可视化工具包 import matplotlib.pyplot as plt %matplotlib inline from sklearn.datasets import load_iris from sklearn.cluster import KMeans import numpy as np import pandas as pd X=load_iris().data clf = KMeans(n_clusters=3,random_state=0) clf.fit(X) label = clf.predict(X) # 颜色和标签列表 colors_list = ['red', 'blue', 'green'] labels_list = ['1','2','3'] x=X for i in range(3): plt.scatter(x[label==i,0], x[label== i,1], s=100,c=colors_list[i],label=labels_list[i]) # 聚类中心点 plt.scatter(clf.cluster_centers_[:,0],clf.cluster_centers_[:,1], s=300,c='black',label='Centroids') plt.legend() plt.xlabel('Annual Income (k$)') plt.ylabel('Spending Score (1-100)') plt.show()
六、获取kmeans特征权重,特征贡献度
有时候我们需要看一下,哪个特征对kmeans贡献最大,但是如果是使用pca之后的数据做模型,那么就有点难计算,但是pca也是根据变量方差去选择,也即是说第一主成分的选择是根据最大方差去选择,了解这个或许还可以计算出来,
但是我们主要说非pca之后的:
#验证过,该属性确实可以计算出来 estimator=KMeans() estimator.fit(X) res=estimator.__dict__ print res['cluster_centers_']