这个函数的作用为:对于不同大小的训练集,确定交叉验证训练和测试的分数。一个交叉验证发生器将整个数据集分割k次,分割成训练集和测试集。不同大小的训练集的子集将会被用来训练评估器并且对于每一个大小的训练子集都会产生一个分数,然后测试集的分数也会计算。然后,对于每一个训练子集,运行k次之后的所有这些分数将会被平均
sklearn.model_selection.learning_curve(estimator, X, y, *, groups=None, train_sizes=array([0.1, 0.33, 0.55, 0.78, 1. ]),
cv=None, scoring=None, exploit_incremental_learning=False, n_jobs=None, pre_dispatch='all', verbose=0, shuffle=False, random_state=None, error_score=nan, return_times=False)
参数:
(1)estimator:基模型(如决策树、逻辑回归等)
(2)x:特征值(不包括label),如果不支持df格式,我们就用df.values
(3)y:label 目标值
(4)groups:将数据集拆分为训练/测试集时使用的样本的标签分组
(5)train_sizes:array-like, shape (n_ticks,), dtype float or int:训练示例的相对或绝对数量,将用于生成学习曲线。如果dtype为float,默认为np.linspace(0.1,1.0,5)
(6)cv:交叉验证折数,默认的5折交叉验证,如果基模型是分类器,且y是二分类或者是多分类,这使用StratifiedKFold,其他情况默认使用KFold
后面的就不补充了
返回:
train_sizes_abs:array, shape = (n_unique_ticks,), dtype int:用于生成learning curve的训练集的样本数。由于重复的输入将会被删除,所以ticks可能会少于n_ticks.
train_scores : array, shape (n_ticks, n_cv_folds):在训练集上的分数
test_scores : array, shape (n_ticks, n_cv_folds):在测试集上的分数
使用鸢尾花作为例子
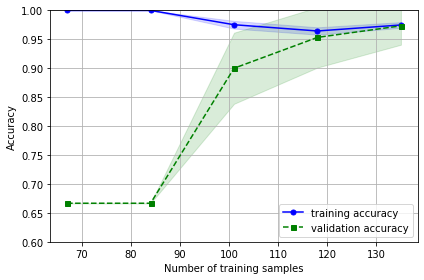
import pandas as pd import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import load_iris from sklearn.model_selection import learning_curve from sklearn.linear_model import LogisticRegression # 用于模型预测 iris=load_iris() x=iris.data y=iris.target train_sizes, train_scores, test_scores = learning_curve(estimator= LogisticRegression(random_state=1), X=x, y=y, train_sizes=np.linspace(0.5, 1.0, 5), #在0.1和1间线性的取10个值 cv=10, n_jobs=1) train_sizes, train_scores, test_scores train_mean = np.mean(train_scores, axis=1) train_std = np.std(train_scores, axis=1) test_mean = np.mean(test_scores, axis=1) test_std = np.std(test_scores, axis=1) plt.plot(train_sizes, train_mean, color='blue', marker='o', markersize=5, label='training accuracy') plt.fill_between(train_sizes, train_mean + train_std, train_mean - train_std, alpha=0.15, color='blue') plt.plot(train_sizes, test_mean, color='green', linestyle='--', marker='s', markersize=5, label='validation accuracy') plt.fill_between(train_sizes, test_mean + test_std, test_mean - test_std, alpha=0.15, color='green') plt.grid() plt.xlabel('Number of training samples') plt.ylabel('Accuracy') plt.legend(loc='lower right') plt.ylim([0.6, 1.0]) plt.tight_layout() plt.show()