KNN（K近邻法）算法原理

 

一、K近邻概述

k近邻法（k-nearest neighbor, kNN）是一种基本分类与回归方法（有监督学习的一种），KNN(k-nearest neighbor algorithm)算法的核心思想是如果一个样本在特征空间中的k（k一般不超过20）个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。简单地说，K-近邻算法采用测量不同特征值之间的距离方法进行分类。

通常，在分类任务中可使用“投票法”，即选择这k个实例中出现最多的标记类别作为预测结果；在回归任务中可使用“平均法”，即将这k个实例的实值输出标记的平均值作为预测结果；还可基于距离远近进行加权平均或加权投票，距离越近的实例权重越大。
k近邻法不具有显式的学习过程，事实上，它是懒惰学习（lazy learning）的著名代表，此类学习技术在训练阶段仅仅是把样本保存起来，训练时间开销为零，待收到测试样本后再进行处理

K近邻算法的优缺点：

• 优点：精度高、对异常值不敏感、无数据输入假定
• 缺点：计算复杂度高、空间复杂度高
• 适用数据范围：数值型和标称型

二、K近邻法的三要素

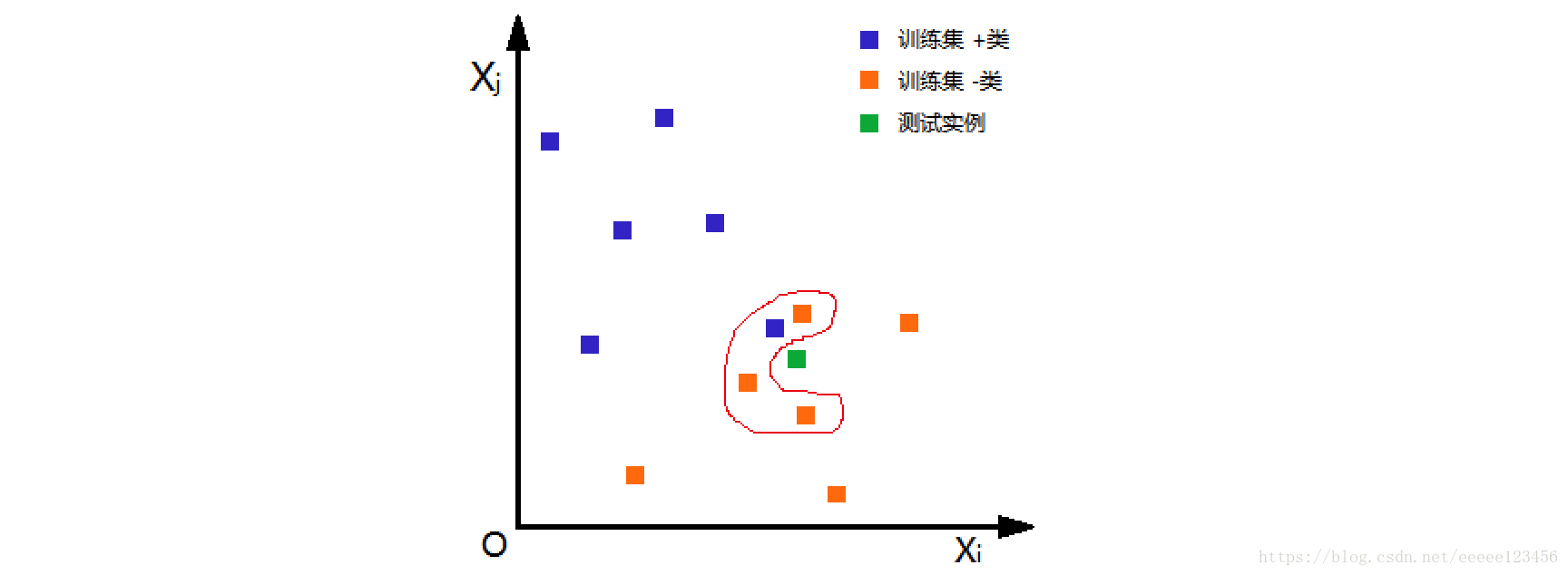
距离度量、k值的选择及分类决策规则是k近邻法的三个基本要素。根据选择的距离度量（如曼哈顿距离或欧氏距离），可计算测试实例与训练集中的每个实例点的距离，根据k值选择k个最近邻点，最后根据分类决策规则将测试实例分类。

根据欧氏距离，选择k=4个离测试实例最近的训练实例（红圈处），再根据多数表决的分类决策规则，即这4个实例多数属于“-类”，可推断测试实例为“-类”。
k近邻法1968年由Cover和Hart提出

 1.距离度量

特征空间中的两个实例点的距离是两个实例点相似程度的反映。K近邻法的特征空间一般是n维实数向量空间Rn。使用的距离是欧氏距离，但也可以是其他距离，如更一般的Lp距离或Minkowski距离

Minkowski距离（也叫闵氏距离）：

• 当p=1时，得到绝对值距离，也称曼哈顿距离（Manhattan distance），在二维空间中可以看出，这种距离是计算两点之间的直角边距离，相当于城市中出租汽车沿城市街道拐直角前进而不能走两点连接间的最短距离，绝对值距离的特点是各特征参数以等权参与进来，所以也称等混合距离
• 当p=2时，得到欧几里德距离（Euclidean distance），就是两点之间的直线距离（以下简称欧氏距离）。欧氏距离中各特征参数是等权的
• 当p趋向无穷∞，得到切比雪夫距离

设特征空间X是n维实数向量空间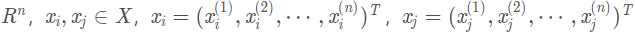，的L_p 距离定义为

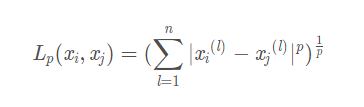
这里p≥1。
当p=1时，称为曼哈顿距离（Manhattan distance），即

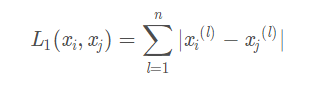
 当p=2时，称为欧氏距离（Euclidean distance），即

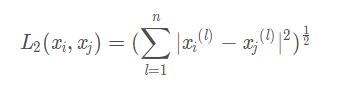
 当p=∞时，它是各个坐标距离的最大值，即

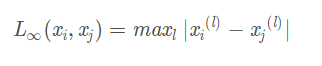
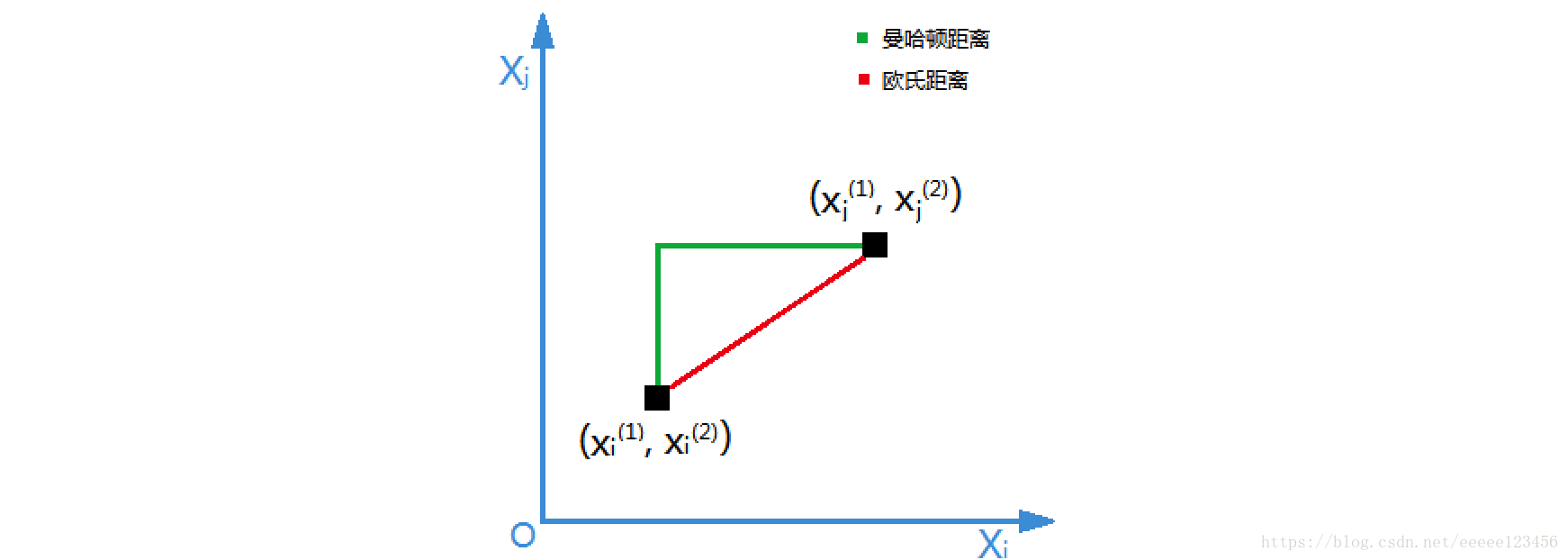
 证明：以二维实数向量空间（n=2）为例说明曼哈顿距离和欧氏距离的物理意义

 （1）曼哈顿距离

 

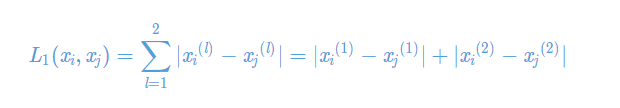
 （2）欧氏距离

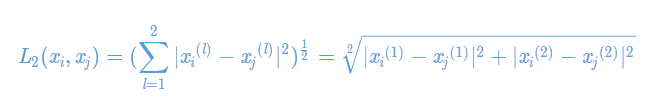
2.K值的选择

k值的选择会对k近邻法的结果产生重大影响。在应用中，k值一般取一个比较小的数值，通常采用交叉验证法来选取最优的k值

说明一下：我举这个例子，虽说不是k近邻，但是我们可以操作这种方式去找到比较适合的参数，当然也可以使用网格搜索法

from sklearn.ensemble import GradientBoostingClassifier 
depth_ = [1, 2, 3, 4, 5, 6, 7, 8]
scores = []
for depth in depth_:
    clf = GradientBoostingClassifier(n_estimators=100, max_depth=depth, random_state=0)
    test_score = cross_val_score(clf, train_df, y_train, cv=10, scoring="precision")
    scores.append(np.mean(test_score))
plt.plot(depth_, scores)

3.分类决策规则

k近邻法中的分类决策规则往往是多数表决，即由输入实例的k个邻近的训练实例中的多数类，决定输入实例的类

我自己编写了一下自定义的knn ：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 导入KNN分类器
from sklearn.neighbors import KNeighborsClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from collections import Counter

def knn(test_data,train_data,train_y,k):
    '''
    目的就是knn
    里面的距离计算使用的是欧氏距离

    '''
    data_size=train_data.shape[0]
    test_y=[]
    for i in test_data:
        diffmat=np.tile(i,(data_size,1))-train_data
        sqdiffmat=diffmat**2
        sqdistance=sqdiffmat.sum(axis=1)
        distance=sqdistance**0.5  #计算测试和每个训练集的距离
        sort_index=distance.argsort()
        for_label=[]
        for j in range(k):
            voteilabel=train_y[sort_index[j]]  #
            for_label.append(voteilabel)
        t_label=Counter(for_label).most_common(1)[0][0]
        test_y.append(t_label)
    return test_y

def knn_acuuary(test_y,test_data,train_data,train_y,k):
    df=pd.DataFrame()
    df['y']=knn(test_data,train_data,train_y,k)
    df['test_y']=test_y
    l=len(test_y)
    acuuary=len(df[df['y']==df['test_y']])/l
    return acuuary,df




if __name__=='__main__':

    # 载入鸢尾花数据集
    # iris是一个对象类型的数据，其中包括了data（鸢尾花的特征）和target（也就是分类标签）
    iris = datasets.load_iris()
    x=pd.DataFrame(iris.data)
    y=iris.target    
    print(x.shape, y.shape)  # (150, 4) (150,)    

    # 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2)  # 8:2
    print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
    acuuary,df=knn_acuuary(y_test,x_test.values,x_train.values,y_train,5)
    #print(acuuary,df)
    print(acuuary)

三、K近邻法的实现：KD树

       实现k近邻法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索，这点在特征空间的维数大及训练数据容量大时尤其必要。
    k近邻法最简单的实现方法是线性扫描（linear scan），这时要计算输入实例与每一个训练实例的距离，当训练集很大时，计算非常耗时。为了提高k近邻法搜索的效率，可以考虑使用特殊的结构存储训练数据，以减少计算距离的次数。具体方法很多，下面介绍其中的kd树方法（kd树是存储k维空间数据的树结构，这里的k与k近邻法的k意义不同）。

 1.kd树算法原理

       k-d tree是每个节点均为k维数值点（即是说每个节点都是一个坐标（x1,x2...xn））的二叉树，其上的每个节点代表一个超平面，该超平面垂直于当前划分维度的坐标轴，并在该维度上将空间划分为两部分，一部分在其左子树，另一部分在其右子树。即若当前节点的划分维度为d，其左子树上所有点在d维的坐标值均小于当前值，右子树上所有点在d维的坐标值均大于等于当前值，本定义对其任意子节点均成立
    通常，依次选择坐标轴对空间切分，选择训练实例点在选定坐标轴上的中位数（一组数据按大小顺序排列起来，处于中间的一个数或最中间两个数的平均值。本文在最中间有两个数时选择最大值作中位数）为切分点，这样得到的kd树是平衡的。注意，平衡的kd树搜索时未必是最优的。

 2.KD树构建

一个平衡的k-d tree，其所有叶子节点到根节点的距离近似相等。但一个平衡的k-d tree对最近邻搜索、空间搜索等应用场景并非是最优的。
常规的k-d tree的构建过程为：循环依序取数据点的各维度来作为切分维度，取数据点在该维度的中值作为切分超平面，将中值左侧的数据点挂在其左子树，将中值右侧的数据点挂在其右子树。递归处理其子树，直至所有数据点挂载完毕

切分维度选择优化

构建开始前，对比数据点在各维度的分布情况，数据点在某一维度坐标值的方差越大分布越分散，方差越小分布越集中。从方差大的维度开始切分可以取得很好的切分效果及平衡性

中值选择优化

第一种，算法开始前，对原始数据点在所有维度进行一次排序，存储下来，然后在后续的中值选择中，无须每次都对其子集进行排序，提升了性能。
第二种，从原始数据点中随机选择固定数目的点，然后对其进行排序，每次从这些样本点中取中值，来作为分割超平面。该方式在实践中被证明可以取得很好性能及很好的平衡性

以二维平面点(x,y)的集合(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)为例结合下图来说明k-d tree的构建过程

a）构建根节点时，此时的切分维度为x，如上点集合在x维从小到大排序为(2,3)，(4,7)，(5,4)，(7,2)，(8,1)，(9,6)；其中值为(7,2)。（注：2,4,5,7,8,9在数学中的中值为(5 + 7)/2=6，但因该算法的中值需在点集合之内，所以本文中值计算用的是len(points)//2=3, points[3]=(7,2)）
b）(2,3)，(4,7)，(5,4)挂在(7,2)节点的左子树，(8,1)，(9,6)挂在(7,2)节点的右子树。
c）构建(7,2)节点的左子树时，点集合(2,3)，(4,7)，(5,4)此时的切分维度为y，中值为(5,4)作为分割平面，(2,3)挂在其左子树，(4,7)挂在其右子树。
d）构建(7,2)节点的右子树时，点集合(8,1)，(9,6)此时的切分维度也为y，中值为(9,6)作为分割平面，(8,1)挂在其左子树。至此k-d tree构建完成

树的深度应该等于数据集的维度（也就是特征个数），也就是k=特征个数=树的深度