幂函数

目录

1. 基本概念
2. python画图
3. 定义域和值域
4. 性质
5. 单调区间
6. 特性

一、基本概念

幂函数是基本初等函数之一。
一般地，y = x^a （α为有理数）的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数。例如函数y = x⁰  、y =  x¹ 、y = x² 、y = x^-1 （注：y = x^-1 =1/x、y = x⁰时x≠0）等都是幂函数。

二、python画图

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

x=np.linspace(-5,5, 500,dtype=float)
y=np.power(x,2)
y1=np.power(x,3)
y2=np.power(x,0.5)
plt.plot(x,y,color='r',label='y=x^2')
plt.plot(x,y1,color='g',label='y=x^3')
plt.plot(x,y2,color='y',label='y=x^0.5')
plt.legend(loc='upper right')#把图例放在右上角
plt.show()

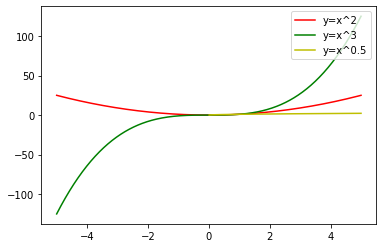
三、定义域和值域

幂函数的一般形式是 y = x^a  ，其中，a可为任何常数

这个数据太复杂了，想看定义域和值域，只看画图看吧，我把画图函数放在这里

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

def mi_plot(a):
    x=np.linspace(-5,5, 500,dtype=float)
    y=np.power(x,a)
    b='y=x^'+str(a)
    plt.plot(x,y,color='r',label=b)
    plt.legend(loc='upper right')#把图例放在右上角
    plt.show()

mi_plot(0)
mi_plot(1/2)
mi_plot(1)
mi_plot(1.5)
mi_plot(2)
mi_plot(2.5)
mi_plot(3)

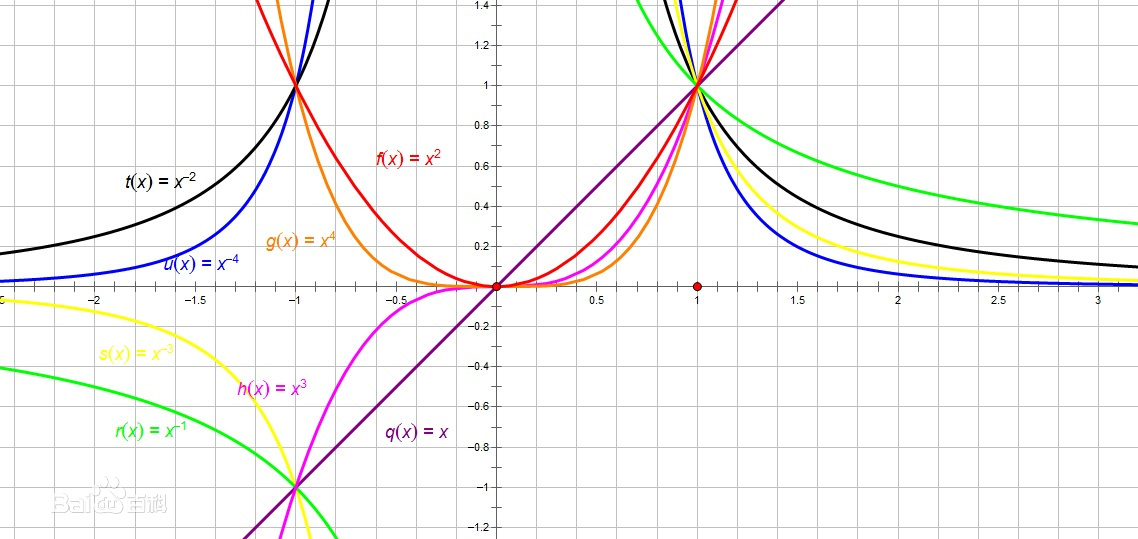
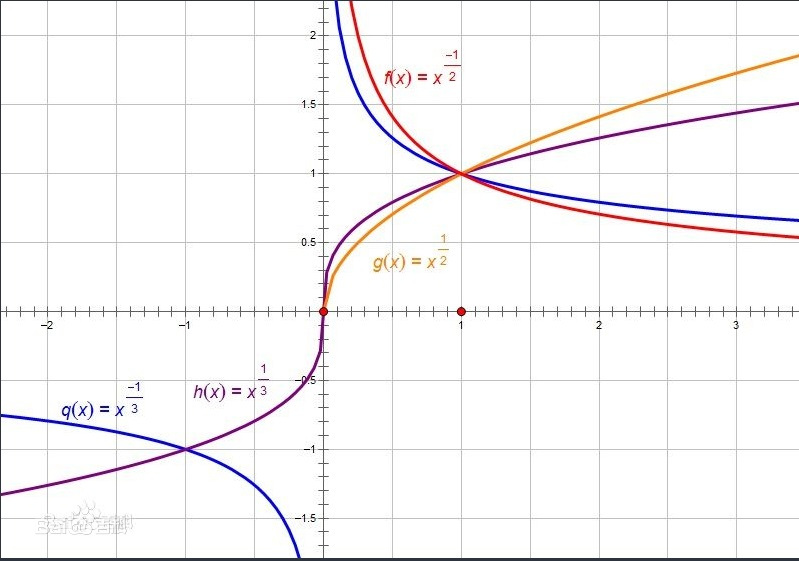
四、性质

正值性质

当α>0时，幂函数y=x^a  有下列性质：

a、图像都经过点（1,1）（0,0）；

b、函数的图像在区间[0,+∞）上是增函数；

c、在第一象限内，α>1时，导数值逐渐增大；α=1时，导数为常数；0<α<1时，导数值逐渐减小，趋近于0（函数值递增）；

负值性质

当α<0时，幂函数y=x^a  有下列性质：

a、图像都通过点（1,1）；

b、图像在区间（0，+∞）上是减函数。

c、在第一象限内，有两条渐近线（即坐标轴），自变量趋近0，函数值趋近+∞，自变量趋近+∞，函数值趋近0。

零值性质

当α=0时，幂函数y=x^a有下列性质：

a、y=x^a的图像是直线y=1去掉一点（0,1）。它的图像不是直线。

五、单调区间

单调区间：
当α为整数时，α的正负性和奇偶性决定了函数的单调性：
①当α为正奇数时，图像在定义域为R内单调递增；

mi_plot(3)

②当α为正偶数时，图像在定义域为第二象限内单调递减，在第一象限内单调递增；

mi_plot(4)

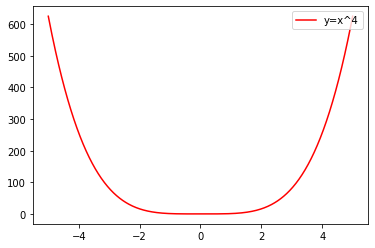
③当α为负奇数时，图像在第一三象限各象限内单调递减（但不能说在定义域R内单调递减）；

mi_plot(-1)

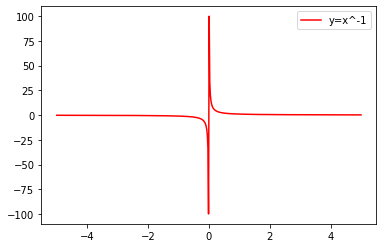
④当α为负偶数时，图像在第二象限上单调递增，在第一象限内单调递减。

mi_plot(-2)

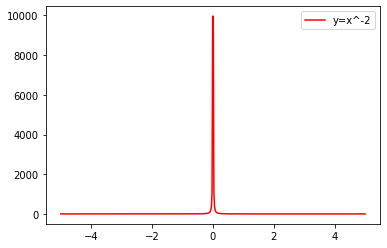
当α为分数时（且分子为1），α的正负性和分母的奇偶性决定了函数的单调性：
①当α>0，分母为偶数时，函数在第一象限内单调递增；

mi_plot(1/2)

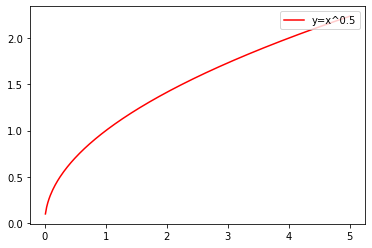
②当α>0，分母为奇数时，函数在第一三象限各象限内单调递增；

mi_plot(1/5)

③当α<0，分母为偶数时，函数在第一象限内单调递减；

mi_plot(-1/2)

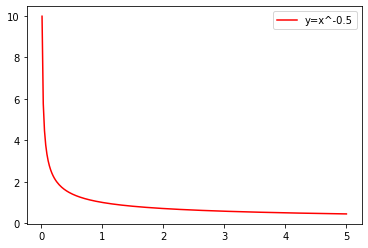
④当α<0，分母为奇数时，函数在第一三象限各象限内单调递减（但不能说在定义域R内单调递减）；

mi_plot(-1/3)

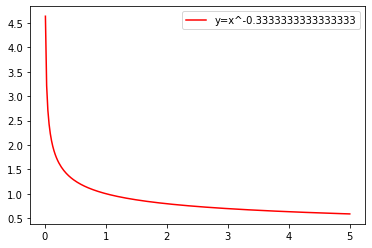
六、特性

对于α的取值为非零有理数，有必要分成几种情况来讨论各自的特性：
首先我们知道如果 a = p/q，q和p都是整数，则 :

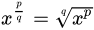
如果q是奇数，函数的定义域是R;如果q是偶数，函数的定义域是[0,+∞）。
当指数α是负整数时，设α=-k，则 ，显然x≠0，函数的定义域是（－∞，0）∪（0,+∞）。因此可以看到x所受到的限制来源于两点，一是有可能作为分母而不能是0，一是有可能在偶数次的根号下而不能为负数，那么我们就可以知道：
α小于0时，x不等于0；
α的分母为偶数时，x不小于0；
α的分母为奇数时，x取R。