X^n+1=0上的FFT和IFFT（基2）——C语言实现

我们一般意义上学习的FFT都是基于的，即FFT中的单位根我们取的是，但是在某些情况下我们需要上的FFT和IFFT变换。

1、直接想到的思路是把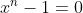的根替换成的根。

解法：的根可以使用的2n个根中的奇数次根得到，即，但是这种做法在FFT运算中可行，在IFFT逆运算下则不可行，我们一般的IFFT运算时把替换成，并且最后除以一个n得到IFFT运算的结果。如下

 

   

 

但是我们需要在上做IFFT变换的时候不能简单的把根替换成，因为根据FFT的点值多项式的形式，只有根是的形式的时候，才可以使用

因为根是 的形式的时候，

在上IFFT求逆的时候，不成立，直接替换根的做法是不可行的。

 

2、新的做法，扩展到2n次

设 ,,,f(x)是n次多项式。

令:

则有：

 

FFT计算步骤：

(1)计算

(2)此时F(x)是m次方的，计算F(x)在上的FFT（就是以前一般形式的FFT）

(3)输出F(x) 的FFT变换之后的奇数项，即为f(x)在上的FFT结果

 

IFFT计算步骤：

设是f(x)在上的FFT结果

(1)将扩展，使其奇数项为，偶数项为0，扩展到2n次

(2)使用2n阶IFFT求出扩展后多项式的逆变换的值

(3)设（2）中逆变换对应的扩展多项式逆变换为,令

还原出来的n次

 

大致整体思路就是扩展到2n次，然后使用上的FFT和IFFT求出上的FFT和IFFT变换

下面贴C语言代码：

#include "pch.h"
#define _CRT_SECURE_NO_WARNINGS
#include "stdlib.h"
#include "math.h"
#include "stdio.h"


#define N 8
#define MAXN 100

#define Pi  3.1415927   //定义圆周率Pi
#define LEN sizeof(struct Compx)  //定义复数结构体大小

//-----定义复数结构体-----------------------
typedef struct Compx
{
	double real;
	double imag;
}Compx;

//-----复数乘法运算函数---------------------
struct Compx mult(struct Compx b1, struct Compx b2)
{
	struct Compx b3;
	b3.real = b1.real*b2.real - b1.imag*b2.imag;
	b3.imag = b1.real*b2.imag + b1.imag*b2.real;
	return(b3);
}

//-----复数减法运算函数---------------------
struct Compx sub(struct Compx a, struct Compx b)
{
	struct Compx c;
	c.real = a.real - b.real;
	c.imag = a.imag - b.imag;
	return(c);
}

//-----复数加法运算函数---------------------
struct Compx add(struct Compx a, struct Compx b)
{
	struct Compx c;
	c.real = a.real + b.real;
	c.imag = a.imag + b.imag;
	return(c);
}

void fft(Compx *a, int n, int inv);
void fft_1(Compx *a, int n, int inv);

int main()
{
	int i;

	int x[N] = { 0 }, y[N] = { 0 };

	printf("
N=%d
", N);
	printf("
输入两个多项式的系数，输入系数为N多项式长度的一半
");
	printf("
输入第一个多项式的系数
");
	for (i = 0; i < N / 2; i++)
	{
		scanf("%d", &x[i]);
	}

	struct  Compx * a = (struct Compx *)malloc(N*LEN);			//为结构体分配存储空间
	struct  Compx * b = (struct Compx *)malloc(N*LEN);
	struct  Compx * c = (struct Compx *)malloc(N*LEN);
	struct  Compx * F = (struct Compx *)malloc(2*N*LEN);

	//初始化======================================= 
	printf("
a多项式初始化：
");
	for (i = 0; i < N; i++)
	{
		a[i].real = x[i];
		a[i].imag = 0;
		printf("%.4f ", a[i].real);
		printf("+%.4fj  ", a[i].imag);
		printf("
");
	}

	/*--------------x^2n-1=0的解法----start----------*/
	printf("
--------------------------FFT---------------------------------
");
	int m = 2 * N;
	int n = N;
	double f[2 * N] = { 0 };

	for (i = 0; i < N; i++) {
		f[i] = 0.5 * x[i];
	}
	for (i = N; i < 2*N; i++) {
		f[i] = -0.5 * x[i-N];
	}

	printf("
f多项式初始化：
");
	for (i = 0; i < 2*N; i++)
	{
		F[i].real = f[i];
		F[i].imag = 0;
		printf("%.4f ", F[i].real);
		printf("+%.4fj  ", F[i].imag);
		printf("
");
	}

	fft(F, m, 1);
	printf("
F多项式FFT计算结果：
");
	for (i = 0; i < 2*N; i++)
	{
		printf("%.4f ", F[i].real);
		printf("+%.4fj  ", F[i].imag);
		printf("
");
	}

	for (i = 0; i < N; i++ ) {
		a[i] = F[2 * i + 1];
	}


	printf("
--------------------------IFFT---------------------------------
");
	fft(F, m, -1);
	for (i = 0; i < m; i++) {
		F[i].real = F[i].real / m;
		F[i].imag = F[i].imag / m;
	}
	printf("
F多项式IFFT计算结果：
");
	for (i = 0; i < 2 * N; i++)
	{
		printf("%.4f ", F[i].real);
		printf("+%.4fj  ", F[i].imag);
		printf("
");
	}

	//F(x)的低次
	double temp_low[N] = { 0 };
	double temp_high[N] = { 0 };
	for (i = 0; i < N; i++)
	{
		temp_low[i] = F[i].real;
	}
	for (i = N; i < 2*N; i++)
	{
		temp_high[i-N] = F[i].real;
	}
	double res[N] = { 0 };
	for (i = 0; i < N; i++)
	{
		res[i] = temp_low[i] - temp_high[i];
	}

	printf("
IFFT计算结果：
");
	for (i = 0; i < N; i++)
	{
		printf("%.4f", res[i]);
		printf("
");
	}





	/*--------------x^2n+1=0的解法----end----------*/

	//fft_1(a, N, 1);

	printf("
第一个多项式FFT计算结果：
");
	for (i = 0; i < N; i++)
	{
		printf("%.4f ", a[i].real);
		printf("+%.4fj  ", a[i].imag);
		printf("
");
	}

	return 0;
}


//x^n+1=0的FFT形式
void fft_1(Compx *a, int n, int inv) {
	if (n == 1)return;
	int mid = n / 2;
	static Compx b[MAXN];
	int i;
	for (i = 0; i < mid; i++) {
		b[i] = a[i * 2];
		b[i + mid] = a[i * 2 + 1];
	}

	for (i = 0; i < n; i++)
		a[i] = b[i];
	fft(a, mid, inv);
	fft(a + mid, mid, inv);//分治
	for (i = 0; i < mid; i++)
	{
		Compx x;
		x.real = cos(2 * Pi*(2*i+1) / (2*n));
		x.imag = inv * sin(2 * Pi*(2 * i + 1) / (2*n));

		b[i] = add(a[i], mult(x, a[i + mid]));
		b[i + mid] = sub(a[i], mult(x, a[i + mid]));
	}
	for (i = 0; i < n; i++)
		a[i] = b[i];
}

//x^n-1=0的FFT形式
void fft(Compx *a, int n, int inv) {
	if (n == 1)return;
	int mid = n / 2;
	static Compx b[MAXN];
	int i;
	for (i = 0; i < mid; i++) {
		b[i] = a[i * 2];
		b[i + mid] = a[i * 2 + 1];
	}

	for (i = 0; i < n; i++)
		a[i] = b[i];
	fft(a, mid, inv);
	fft(a + mid, mid, inv);//分治
	for (i = 0; i < mid; i++)
	{
		Compx x;
		x.real = cos(2 * Pi*i / n);
		x.imag = inv * sin(2 * Pi*i / n);

		b[i] = add(a[i], mult(x, a[i + mid]));
		b[i + mid] = sub(a[i], mult(x, a[i + mid]));
	}
	for (i = 0; i < n; i++)
		a[i] = b[i];
}