随便翻到的一道题......
这道题是用向量叉积求多边形面积。
首先讲一下向量叉积(也叫外积)。
设两个向量的坐标表示为(x1,y1)、(x2,y2)。
那么它们的叉积为x1*y2-x2*y1。
其几何意义为两个向量所成的平行四边形的面积(浅蓝色部分)。
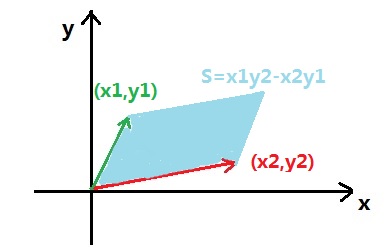
两个向量的叉积与这两个向量都垂直,且有正负之分。
叉积的正负取决于两向量夹角sin值的正负(图中叉积均为:绿向量×红向量)。
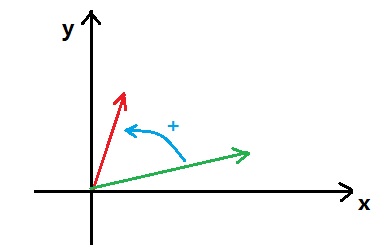

对于两个点A、B以及原点O,向量OA与向量OB的叉积的一半代表三角形OAB的面积。
这样我们就能通过这个把多边形分割成三角形,进而求出多边形的面积。
对于下面这个四边形ABCD:

S(ABCD)=S(OAB)+S(OBC)-S(OCD)-S(ODA)。
我们沿着多边形走一周,依次加上(或减掉)相邻的两个顶点与原点形成的三角形的面积就行。
三角形的面积就用叉积算嘛。
而且你可以发现向量的叉积特别可爱,都不需要你判断是该加上还是该减掉。
叉积算出来是正的,对面积的贡献就为正;是负的,对面积的贡献就为负。
最后别忘了最后一个点和第一个点也要求一下叉积。
所以多边形的面积就这么愉快地算出来啦~
1 #include<cstdio> 2 3 int n; 4 double b,ans; 5 6 struct vec 7 { 8 double x,y; 9 }a[1000005]; 10 11 double cross(vec q,vec w) 12 { 13 return q.x*w.y-w.x*q.y; 14 } 15 16 int main() 17 { 18 scanf("%d%lf",&n,&b); 19 for(int i=1;i<=n;i++)scanf("%lf%lf",&a[i].x,&a[i].y); 20 a[n+1]=a[1]; 21 for(int i=1;i<=n;i++)ans+=cross(a[i],a[i+1]); 22 ans=ans*b*0.50; 23 if(ans<0)ans=-ans; 24 printf("%.4lf",ans); 25 return 0; 26 }