1. 聚类(Clustering)
- 监督学习:发现数据属性和类别属性之间的关联模式。并通过利用这些模式用来预测未知数据实例的类别属性。
- 无监督学习:数据没有目标属性。发现数据中存在的内在结构及规律。
无监督学习中研究最多、应用最广的是聚类。常见的无监督学习任务还有密度估计(density estimation)、异常检测(anomaly detection)等。
聚类(Clustering)是一种发现数据中的相似群(聚类,clusters)的技术。聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程。一个聚类就是一些数据实例的集合,这个集合中的元素彼此相似;与其他聚类中的元素不同。
聚类的形式定义:

聚类既可以作为一个单独过程,用于找寻数据内在的分布结构。也可以作为分类等其他学习任务的前驱过程。
- 实例1:在营销学中,对客户进行分割,为每组客户指定一个套营销策略,也是采用聚类来完成。
- 实例2:在生物学上,聚类能用于推导植物和动物的分类,对基因进行分类,获得对种群中固有结构的认识。
事实上,聚类是数据挖掘技术中应用最广泛的技术之一。发展历史长,应用领域广泛。比如:医学类、心理学、植物学、社会学、生物学、营销学。近年来,在线文档的快速发展,文本聚类研究成为关注的重点。对给定文本,需要根据它们内容的相似性来进行组织。建立一个主题层次。
聚类算法分为:
- 原型聚类
- 层次聚类
- 密度聚类
距离函数(相似性或相异性):度量两个数据点(对象)的相似程度。
聚类评价的方式有:
- 类内差异(聚类内部距离):最小化
- 类间差异(聚类外部距离):最大化
聚类结果的质量与算法、距离函数和应用领域有很大关系。
2. 原型聚类
原型聚类亦称"基于原型的聚类" (prototype-based clustering),此类算法假设聚类结构能通过一组原型刻画,在现实聚类任务中极为常用.通常情形下,算法先对原型进行初始化,然后对原型进行迭代更新求解.采用不同的原型表示、不同的求解方式,将产生不同的算法.几种著名的原型聚类算法包括K均值算法(K-means)、学习向量量化算法(LVQ)、高斯混合聚类算法。
- K均值算法(K-means)
给定样本集,K均值算法针对聚类所得簇划分最小化平方误差,平方误差刻画了簇内样本围绕均值向量的紧密程度,平方误差值越小则簇内样本相似度越高。但是要找到平方误差的最优解需要考察样本集中所有可能的簇划分,这是一个NP难问题。因此,K-均值算法采用了贪心策略,通过迭代优化来近似求解平方误差。
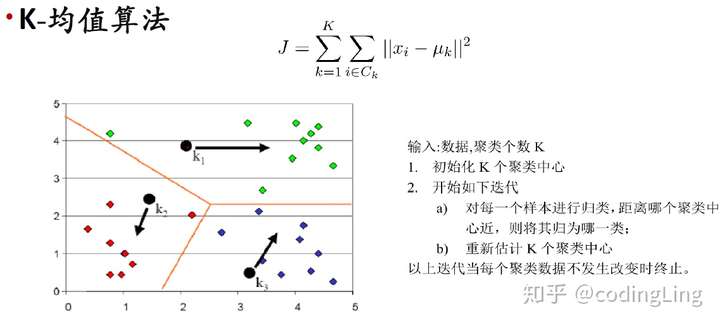
算法流程:

为避免运行时间过长,通常设置一个最大运行轮数或最小调整幅度阈值,若达到最大轮数或调整幅度小于阈值,则停止运行。
K均值算法有大量变体。如k-medoids 算法[Kaufman and Rousseeuw, 1987] 强制原型向量必为训练样本, k-modes 算法[Hua吗, 1998] 可处理离散属性, Fuzzy C -means (简称FCM) [Bezdek, 1981]则是"软聚类" (soft clustering) 算法,允许每个样本以不同程度同时属于多个原型。K均值类算法仅在凸形簇结构上效果较好。(凸形簇结构即形式“椭球”的簇结构)。若采用某种Bregman 距离,则可显著增强此类算法对更多类型簇结构的适用性。引入核技巧则可得到核k 均值(kernel k-means)算法,这与谱聚类(spectral clustering) 有密切联系[Dhillon et al., 2004],后者可看作在拉普拉斯特征映射(Laplacian Eigenmap) 降维后执行k 均值聚类.聚类簇数k 通常需由用户提供,有一些启发式用于自动确定k,但常用的仍是基于不同k 值多次运行后选取最佳结果.
- 学习向量量化算法(LVQ)
与k 均值算法类似,"学习向量量化" (Learning Vector Quantization,简称LVQ)也是试图找到一组原型向量来刻画聚类结构, 但与一般聚类算法不同的是, LVQ 假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类.
LVQ算法如下,每个原型向量代表一个聚类簇,两个原型向量可以代表同一个簇。算法第一行先对原型向量初始化,例如可以对第q个簇,可从对应的同类别样本中随机选取一个作为原型向量。在每一轮选代中,算法随机选取一个有标记训练样本,找出与其距离最近的原型向量,井根据两者的类别标记是否一致来对原型向量进行相应的更新(若类别相同,向该样本的方向靠拢,距离减小为 ,否则远离,距离增大为
).在第12 行中,若算法的停止条件已满足(例如己达到最大迭代轮数,或原型向量更新很小甚至不再更新),则将当前原型向量作为最终结果返回.

该算法对应的对样本空间的簇划分称为“Voronoi剖分”(Voronoi tessellation)。
- 高斯混合聚类
与k 均值、LVQ 用原型向量来刻画聚类结构不同,高斯混合(Mixture-of-Gaussian)聚类采用概率模型来表达聚类原型.
高斯混合分布(如下图中的定义),p(x)是(多元)高斯分布的概率密度函数。

高斯混合聚类的基本假设是:样本的生成过程是由高斯混合分布给出的,也就是说,有若干个(多元)高斯分布,每个分布对应一个被选择的概率,基于这个被选择的概率和若干个分布产生了样本。如果能知道每个样本是由哪个高斯分布产生的,就知道这个样本属于哪个簇了。所以聚类问题转化为判断样本主要是由哪个高斯分布产生的。
具体来说,如果已知选择每个混合成分的先验概率和每个混合成分产生每个样本的概率,要求的是给定样本属于每个混合成分的后验概率,选择后验概率最大的那个作为样本的簇。但其实已知条件不足,两个概率都是未知的,需要进行参数估计,可采用极大似然估计法。



最大化极大似然常采用EM算法。



高斯混合聚类算法:
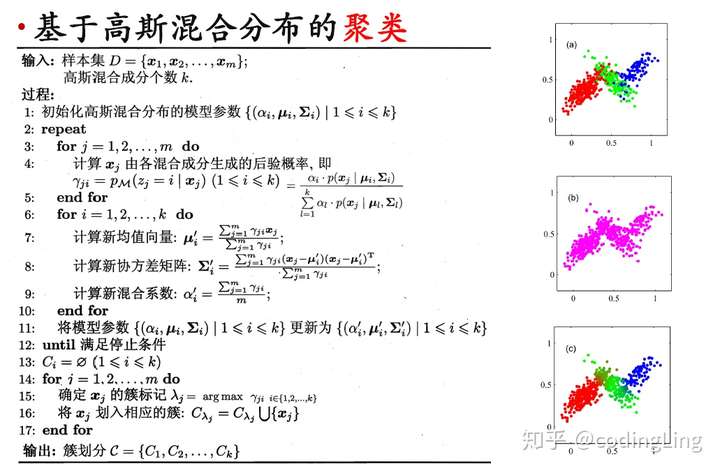
停止条件可以是已达到最大迭代轮数,或似然LL(D)增长很少甚至不再增长。
3.密度聚类
密度聚类亦称"基于密度的聚类" (density-based clustering) ,此类算法假设聚类结构能通过样本分布的紧密程度确定.通常情形下,密度聚类算法从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果.
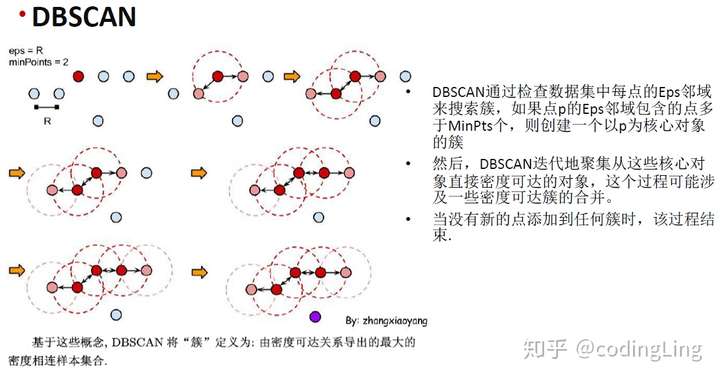
DBSCAN(全称Density-Based Spatial Clustering of Applications with Noise) 是一种著名的密度聚类算法,它基于一组"邻域" (neighborhood)参数 来刻画样本分布的紧密程度.给定数据集
,定义下面几个概念:


DBSCAN对簇的定义:

那么,如何从数据集D中找出满足以上性质的聚类簇呢?实际上,若x为核心对象,由x密度可达的所有样本组成的集合记为 ,则不难证明X即为满足连接性与最大性的簇。
于是,DBSCAN 算法先任选数据集中的一个核心对象为"种子" (seed) ,再由此出发确定相应的聚类簇,算法描述如图所示.在第1 ~7 行中,算法先根据给定的邻域参数 找出所有核心对象;然后在第10~24 行中,以任一核心对象为出发点,找出由其密度可达的样本生成聚类簇,直到所有核心对象均被访问过为止.

密度聚类算法常用的还有OPTICS,DENCLUE等。
4.层次聚类
层次聚类(hierarchical clustering)试图在不同层次对数据集进行划分,从而形成树形的聚类结构. 数据集的划分可采用"自底向上"的聚合策略,也可采用"自顶向下" 的分拆策略.
AGNES(AGglomerative NESting的缩写) 是一种采用自底向上聚合策略的层次聚类算法.它先将数据集中的每个样本看作一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直至达到预设的聚类簇个数.这里的关键是如何计算聚类簇之间的距离.实际上,每个簇是一个样本集合,因此,只需采用关于集合的某种距离即可.例如,给定聚类簇 与
,可通过下面的式子来计算距离:
显然,最小距离由两个簇的最近样本决定,最大距离由两个簇的最远样本决定,而平均距离则由两个簇的所有样本共同决定.当聚类簇距离由 计算时,AGNES算法被相应地称为“单链接”(single-linkage)、“全链接”(complete-linkage)或“均链接”(average-linkage)算法。
AGNES算法描述如图所示。在第1-9 行,算法先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化;然后在第11-23 行, AGNES 不断合并距离最近的聚类簇,并对合并得到的聚类簇的距离矩阵进行更新;上述过程不断重复,直至达到预设的聚类簇数.

一个例子:
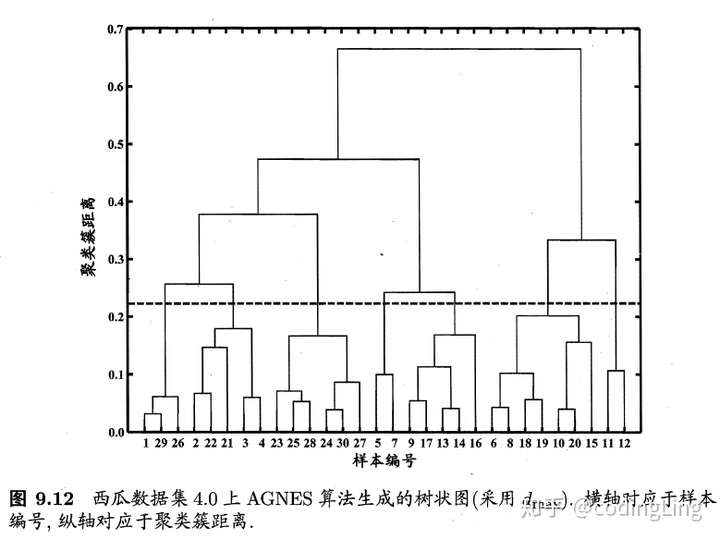
和AGNES相反,DIANA是采用自顶向下的分拆策略。AGNES 和DIANA 都不能对己合并或己分拆的聚类簇进行回溯调整,常用的层次聚类算法如BIRCH [Zhang et al., 1996] 、ROCK [Guha et al., 1999] 等对此进行了改进.
本文介绍了:
- 聚类基本概念
- 原型聚类(包括K均值,LVQ,高斯混合聚类)
- 密度聚类(包括DBSCAN算法)
- 层次聚类(包括AGNES算法)
参考:周志华《机器学习》