1. PSM 简介
在经济学中,我们通常希望评估某项公共政策实施后的效应,为此,我们构建 "处理组" 和 "控制组" 以评估「处理效应 (treatment effect)」。然而,我们的数据通常来自非随机的观察研究中,处理组和控制组的初始条件不完全相同,故存在「选择偏差 ( selection bias)」问题。「倾向得分匹配 (PSM)」法使用倾向得分函数将多维向量的信息压缩到一维,然后根据倾向得分进行匹配。这样可以在既定的可观测特征变量下,使得处理组个体和控制组个体尽可能相似,因而可以缓解处理效应的选择偏差问题。
匹配的思想如下:
假如某个体在处理组,为了找到对照,找至少一个其他各方面与该个体尽量相似但出于控制组的个体,这样两者就有可比性。
倾向得分匹配是指,找一个其他各方面与该个体尽量相似意味着要考虑两个个体的很多方面,让尽可能多的方面尽量相似,而高维匹配并不容易,因为维度越高找一个各方面相似的两个个体越难。为了解决这个问题,Rosenbaum and Rubin (1983)提出了倾向得分的概念。个体的倾向得分是指在个体情况一定的前提下,其进入处理组的概率。倾向得分用logit回归,选择尽可能多的协变量,也就是刚才说的“其他各方面”,类似于回归中的控制变量。计算倾向得分类似于一个降维的过程,把非常多的协变量维度降为一个维度,就是倾向得分,也就是倾向得分综合包含了所有协变量的信息。两个个体的倾向得分非常接近,并不意味着这两个个体的其他属性也接近,这不好判断。不过根据PSM的原理,倾向得分接近就够了,其他属性也接近更好。
2. PSM 的分析过程
2.1 PSM 模型设定
对于个体 ,根据是否进行某项处理可以分为两种结果:表示个体 是否进行某项处理,即 1 表示处理,0表示未处理;
对于离散变量:
gen dv_dum=2 //dv是指变量,dv_dum是指生成自变量的二元变量。 replace dv_dum=0 if dv=0 replace dv_dum=1 if dv=1
如果你的自变量本身就是标为0和1,这一步可以不用,但是如果标为1和2或者其他符号,一定要转换为0和1.
对于连续变量:
quantities dv, gen (dv_dum) nq(3)//根据分位数产生三个虚拟变量,也就是决定选择一个三分位数(上三分位或者下三分位数)为临界值。
replace dv_dum=0 if dv_dum==1 replace dv_dum=0 if dv_dum==2 replace dv_dum=1 if dv_dum==3 //意思是把自变量从小到大排列,最大的1/3作为较高的组,标为1,剩余较小的2/3作为较低的组,标为0.
2.2 PSM 的假设条件
共同支撑假设 (Common Support Assumption)
平行假设 (Balancing Assumption)
2.3 PSM 一般步骤
选择协变量 :尽可能涵盖有影响的相关变量;
获取 PS 值:可以使用 probit 或 logit 模型估计;
检验平行假设是否满足:使得在匹配后的处理组均值和控制组均值较接近,保证数据平衡;
根据 PS值将处理组个体和控制组个体进行配对:匹配的方法有最近邻匹配、半径匹配、核匹配等;
根据匹配后样本计算 ATT 。

3. PSM 的 Stata 实例
*-安装命令
ssc install psmatch2, replace
set seed 10101
gen ranorder=runiform()
sort ranorder
psmatch2 Ln_geodistance_ew $control, out(ln_Cash_ratio1) neighbor(1) ate ties logit common

- out(ln_wage)指明结局变量
- logit指定使用logit模型进行拟合,默认的是probit模型(Logit模型具体分三类:第一类为二分类logistic模型,其对应的命令代码分别为logit;有序多分类logistic模型,其对应的命令代码分别为ologit;无序多分类logistic回归模型,其对应的命令代码为mlogit。)
- neighbor(1)指定按照1:1进行匹配,如果要按照1:3进行匹配,则设定为neighbor(3)
- common强制排除试验组中倾向值大于对照组最大倾向值或低于对照组最小倾向值
- caliper(.05)试验组与匹配对照所允许的最大距离为0.05
- ties强制当试验组观测有不止一个最优匹配时同时记录
- ate 求平均处理效应即求ATT估计值
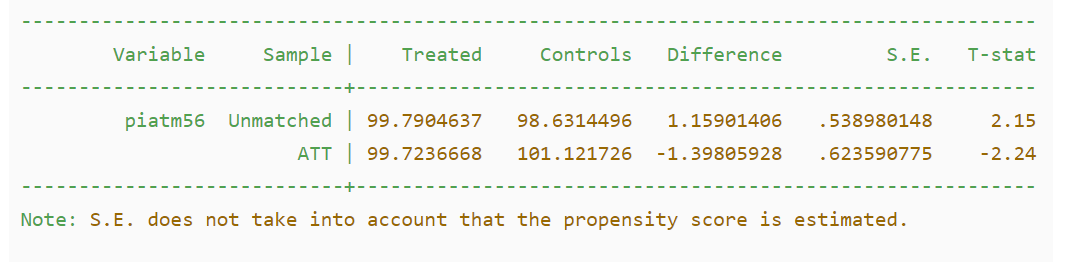

估计结果包含 3 个部分:
第 1 部分是 logit 回归的结果。
第 2 部分是处理组和控制组在匹配前后的差异及其显著性,可以看出,匹配前处理组和控制组差异为 1.15901406,t 值为 2.15,匹配后处理组和控制组差异 -1.39805928,而 t 值为 -2.24。
第 3 部分则汇报观测值共同取值范围情况。在 3100 个观测值中,除了处理组 17 个不在共同取值范围中,其余 3083 个均在共同取值范围中。
重点关注的是ATT的difference值及其T值(实际上这个T值也可不关注),匹配后仍然显著。ATT是个体在干预状态下的平均干预效应,也就是在控制其他匹配变量不变的情况下,自变量从0变为1,因变量的变化。这里ATT的difference意思是在其他匹配变量一致的情况下,自变量是1与自变量是0导致的因变量的差异是1.15个单位,这就是我们要求的系数。接下来根据T值确定p值,这里的T值就是个T检验,T值1.96对应的p值是0.05,一半要求大于1.96,具体可查看T检验统计表。
不过Note提示了,这个表格的标准误差有两个问题,就是没有考虑倾向得分为估计所得的事实,即假设倾向得分为真实值,然后求标准误,并且该标准误假设同方差,也可能不成立。为此,考虑使用自助法求标准误,尽管自助标准误差也未必正确。
打开数据编辑窗口,会发现软件自动生成了几个新变量:
其中_pscore是每个观测值对应的倾向值;
_id是自动生成的每一个观测对象唯一的ID(事实上这列变量即是对_pscore排序);
_treated表示某个对象是否试验组;
_support表示观测对象是否在共同取值范围内
_weight是观测对象用于匹配的频率,如果_weight为空值,那就说明虽然你看上了对方(会有一个匹配对象),但是你并没有被对方看上(对方匹配上的不是你);
_id是自动生成的每一个观测对象唯一的ID;
_n1表示的是他被匹配到的对照对象的_id(如果是1:3匹配,还会生成_n2, _n3);
_pdif表示一组匹配了的观察对象他们概率值的差。
*-考虑自助法估计标准误 set seed 2019 //首先,我们需要产生随机数,对样本进行排序。为了保证结果可复现 bootstrap r(att) r(atu) r(ate),reps(500):psmatch2 distance_ew_high $control, out(ln_Cash_ratio1) neighbor(1) ate ties logit common
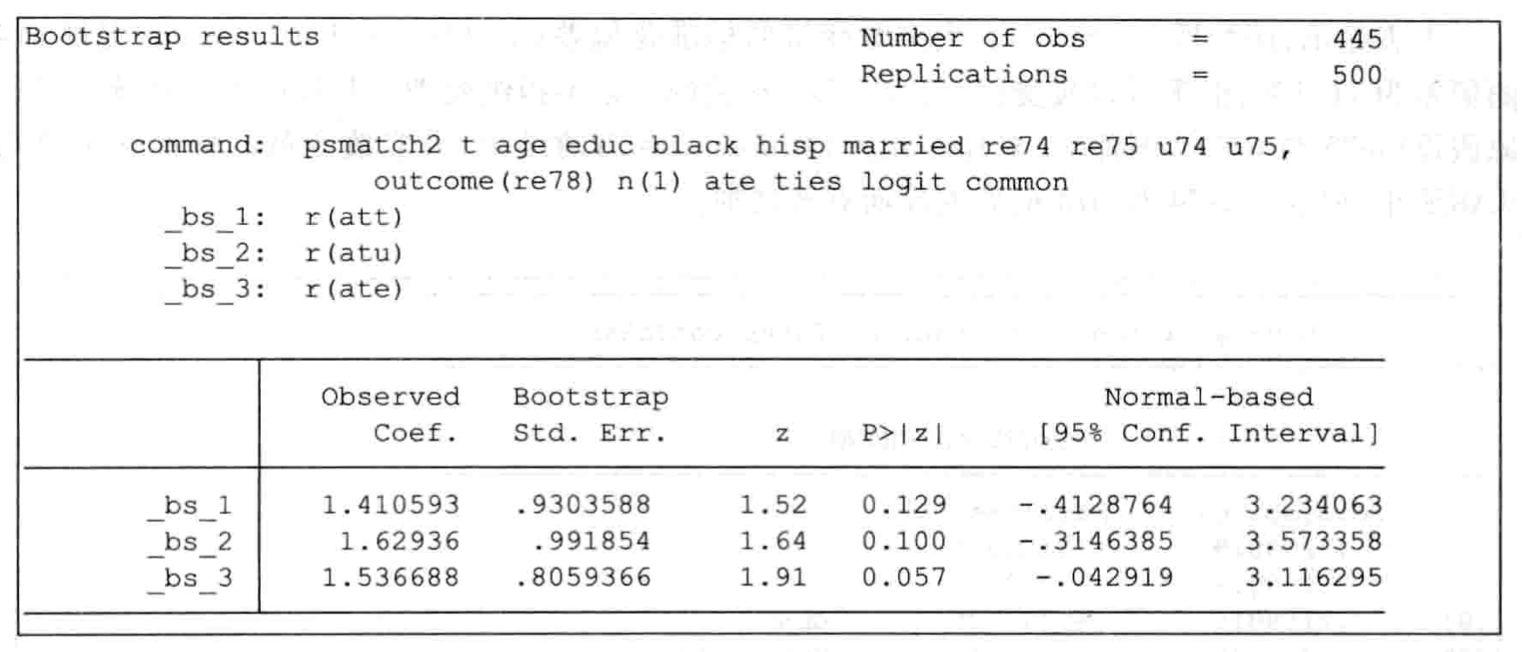
p值求出来了,大于0.1,不显著。这不能说明PSM得到了一个不显著的结果。刚才用的匹配法是一对一匹配,一般来说要把几种常见匹配都试试。陈强书中就把8种匹配法都试了,其中有几种得到了显著的结果。例如用核匹配得到的结果,T值大于1.96,不过这里也应该用自助法求出控制异方差的p值。
*-使用pstest来考查匹配结果是否较好平衡了数据 quiet psmatch2 distance_ew_high $control, out(ln_Cash_ratio1) neighbor(1) ate ties logit common pstest $control,both graph
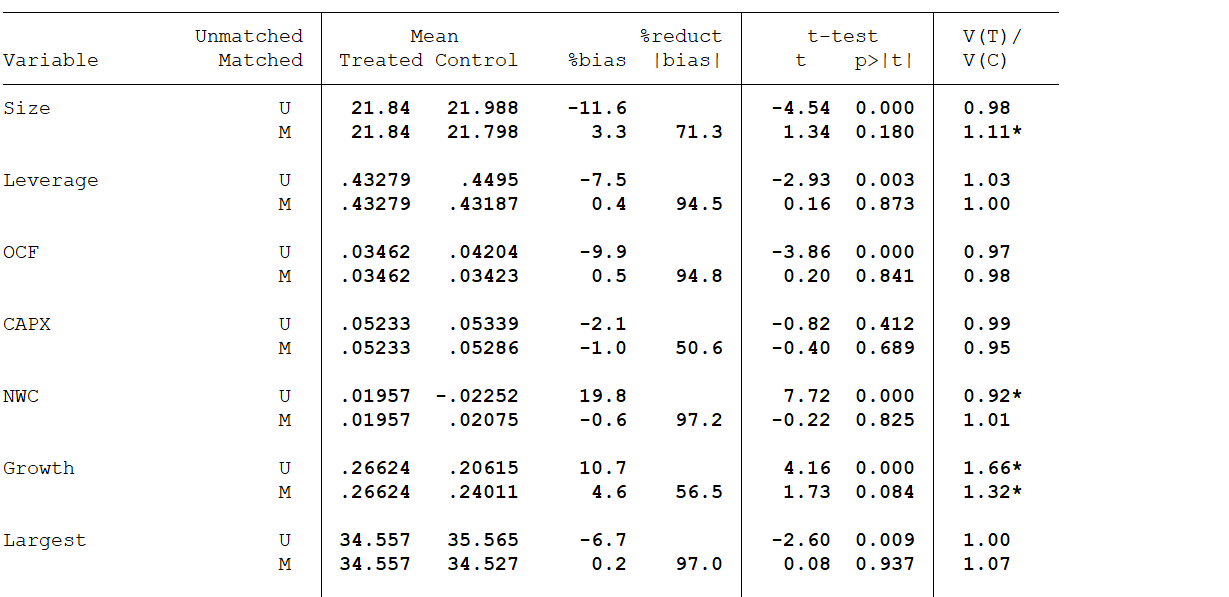
*-画条形图来显示倾向得分匹配的共同取值范围
psgraph
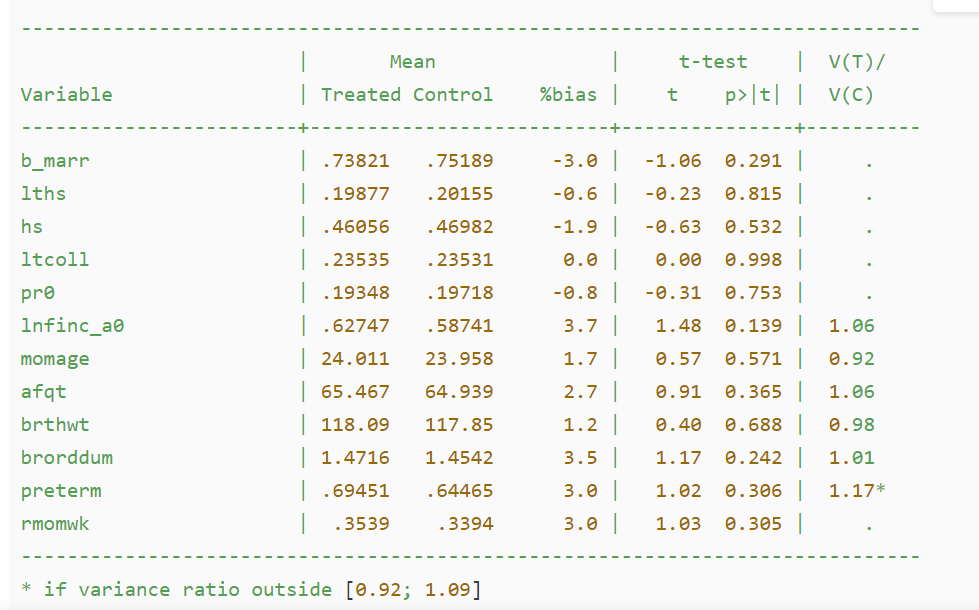
从U到M,P值由显著变为不显著即该变量通过平衡性检验。要得到的结果是每个匹配变量在匹配后,各匹配变量的均值不存在显著差异,其标准化误差(即bias)小于10%,且所有 t 检验结果接受原假设「处理组与控制组无系统差异」,因此平行假设得到满足。以age为例,5.6就是匹配后样本组与控制组的age的标准化差异,小于10%。只有一个变量u74的标准化误差大于10% ,但是也不大很多,并且只有一个变量,因此这个匹配的平衡性可以接受。平衡性检验了可以在匹配前进行,也可以在匹配后进行,只要检验结果可接受。
我们希望能够通过PSM的匹配消除这些差异
PSM的过程在这里就可以结束了,不过有的文章还会用匹配后的数据做个回归,你主分析用的什么回归,这里就用什么回归,只不过样本变了。
*-PSM 匹配样本的回归
drop if _weight==. //_weight是指样本是否参与了匹配,参与了则标为数字,没参与则标为点.,因此这一步是把没参与匹配的样本去掉。
或者可以使用if _weight!=. 在后方添加不影响原数据
xi:reg ln_Cash_ratio1 Ln_geodistance_ew $control i.year i.industry2 if flag==1 ,robust
outreg2 using Table4B,excel drop(_I*) dec(3) tdec(3) bdec(3) alpha(0.01,0.05,0.1) symbol(***,**,*) stats(coef tstat) e(r2_a)
xi:reg ln_Cash_ratio1 Ln_geodistance_ew $control i.year i.industry2 if flag==1 [pw=_weight] //加入了weight加权的结果
outreg2 using Table4B,excel drop(_I*) dec(3) tdec(3) bdec(3) alpha(0.01,0.05,0.1) symbol(***,**,*) stats(coef tstat) e(r2_a)
问题一: 关于一对一匹配和一对多匹配
- 重复和不可重复匹配。不可重复匹配使得每个控制组只能匹配一次,即使该控制组是多个处理组的最佳匹配,这就使得匹配质量降低和样本变小。相反,重复匹配则可以有效避免这些问题,但是在估计处理效应时,需进行加权和调整标准误,以反映匹配次数的影响。当然,也要注意极端控制组被重复匹配多次对推断结果的影响。
- 匹配半径的设定。设定一个相对严格的「半径」值一般可以有效避免「糟糕」的匹配和提高协变量的平衡性。
- 「1 对 1」 和「1 对多」匹配。会计研究中最常见的匹配方法是 1:1 匹配,但是在存在多个合理匹配样本时,「一对多」匹配可以降低抽样方差。与重复匹配一样,在「一对多」匹配时,也需要考虑加权。
经验法则:一对四匹配,均方误差MSE最小。
试一下1:1, 1:2, 1:3的匹配结果进行比较做决定。
问题二:原变量是连续变量手动生成了虚拟变量,在进行回归的时候是进行原回归还是对虚拟变量回归
你主分析用的什么回归,这里就用什么回归,只不过样本变了。匹配后的多元回归,首先要把不参与匹配的样本删除,代码:
drop if _weight==. //_weight是指样本是否参与了匹配,参与了则标为数字,没参与则标为点.,因此这一步是把没参与匹配的样本去掉。 xtset firm year xtreg Y dv_dum controls, fe r
对匹配方法进行对比
1. k近邻匹配,令k=4,节省空间,采用quietly省去结果的汇报
psmatch2 t age educ black hisp married re74 re75 u74 u75,outcome(re78) n(4) ate ties logit common quietly
*上表显示,一对四匹配和一对一匹配类似,下面进行卡尺内一对四匹配,首先计算倾向得分的标准差,乘以0.25
sum _pscore
dis 0.25*r(sd)
0.01979237
*由此可知0.25倍的标准差约等于0.02,将卡尺范围定为0.01,对倾向得分相差1%的观测值进行一对四匹配
psmatch2 t age educ black hisp married re74 re75 u74 u75,outcome(re78) n(4) cal(0.01) ate ties logit common quietly
2. 半径匹配:大多数一对四匹配发生在卡尺0.01范围内,不存在太远的近邻,进行半径(卡尺)匹配
psmatch2 t age educ black hisp married re74 re75 u74 u75,outcome(re78) radius cal(0.01) ate ties logit common quietly
3. 核匹配
psmatch2 t age educ black hisp married re74 re75 u74 u75,outcome(re78) kernel ate ties logit common quietly
4. 局部线性回归匹配(使用默认核函数与带宽)
psmatch2 t age educ black hisp married re74 re75 u74 u75,outcome(re78) llr ate ties logit common quietly
*上表未汇报ATT标准误,采用自助法得到标准误
set seed 2019
bootstrap r(att) r(atu) r(ate),reps(500):psmatch2 t age educ black hisp married re74 re75 u74 u75,outcome(re78) llr ate ties logit common quietly
*根据上表自助标准误,对平均处理效应的三种度量均至少在5%水平上显著
5. 条匹配(同样使用自助法),先安装一个非官方命令spline
findit snp7_1 set seed 2019 bootstrap r(att) r(atu) r(ate),reps(500):psmatch2 t age educ black hisp married re74 re75 u74 u75,outcome(re78) spline ate ties logit common quietly
*估计结果仍然类似,总之,以上各匹配得分结果显示,参加就业培训的平均处理效应为正,在经济意义和统计意义上均显著
6. 马氏匹配,计算异方差稳健标准误
psmatch2 t, outcome(re78) mahal(age educ black hisp married re74 re75 u74 u75) n(4) ai(4) ate
在实践中,并没有明确的规则来限定使用哪种匹配方法,但有一些经验法则可以来参考:
- 如果控制个体不多,应选择又放回匹配
- 如果控制组有较多个体,应选择核匹配
最常用的方法:尝试不同的匹配方法,然后比较它们的结果,结果相似说明很稳健。结果差异较大,就要深挖其中的原因。
但PSM也有局限性:
- 大样本
- 要求处理组和控制组有较大的共同取值范围
- 只控制了可观测的变量,如果存在不可观测的协变量,就会引起“隐性偏差”