- 类
接下来开始我们的程序,首先定义类!
数独是由9*9的81个小格子组成,所以很容易我们会想到把每个小格子看做一个类,整个数独是由81个小格子的9*9的二维数组组成。
1.既然把一个单元格看做一个类,那它具有哪些属性呢?首先肯定需要有一个Value属性表示单元格的值,还没赋值的单元格我们默认将它赋值为0。
2.还有就是上一篇我们提到的Candidate属性表示候选数。候选数当然不一定只有一个,所以他是一个int类型的列表。
3.我们还需要一个DuplicateDel属性,该属性是一个字典类型的列表,主键和值都是int类型,这个属性用来记录被重复删除的候选数的值和次数。在我们后面的程序中会详细说明此属性的意义,为了照顾心急的朋友,在这里我简单说明一下:显然,当我们为单元格填数的时候会相应删除掉与之相关的单元格中该值的候选数,但是如果某些相关单元格中本来就已经没有此候选数,将会重复删除,不会有任何效果。但是一旦我们尝试填数失败返回到上一步,便需要将候选数从这些相关单元格恢复,但是如果是全部恢复,将会和最初状态不一致!所以需要一个属性来记录!越说越糊涂了吧,所以嘛,我都说了后面会详细说明的,暂时先不管这个属性吧,用到再说。
下面是定义好的类,啥也不多说,上图!
 代码
代码
/// 单元格
/// </summary>
class Cell
{
private List<int> candidate; //候选数
public List<int> Candidate
{
get
{
if (candidate == null)
candidate = new List<int>() { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
return candidate;
}
set { candidate = value; }
}
private Dictionary<int, int> duplicateDel; //重复删除候选数次数的记录,以便恢复
public Dictionary<int, int> DuplicateDel
{
get
{
if (duplicateDel == null)
duplicateDel = new Dictionary<int, int>();
return duplicateDel;
}
set { duplicateDel = value; }
}
private int value = 0;
//单元格的值
public int Value { get{ return this.value; }set { this.value = value; } }
}
看上面的代码,很明显,初始化的时候每个单元格的候选数都有1~9这九个数。
定义好类了,下面我们将开始写方法了!
- 方法
我门统一把要用到的所有方法放在一个CellMethod类里面。
SetValue
首先我们先写最简单的方法,那就是为单元格赋值。其实就是把单元格类的Value属性赋值。很显然,这个赋值不能从1~9挨个遍历去试,那样就会向上一篇文章中所说的,我们的电脑又会杯具了。既然我们有候选数这个属性,为什么不用呢?根据候选数的定义,一个单元格所能填的数只能从这个单元格的候选数列表中选。所以我们将会从Candidate属性中选一个值来赋给Value属性。赋值完成后我们还需要把这个赋过的值从Candidate属性中移除。见下图:
 代码
代码
/// 为单元格设定值
/// </summary>
/// <param name="cell">单元格</param>
/// <returns>返回结果</returns>
public bool SetValue(Cell cell)
{
if (cell.Value != 0)
{
throw new InvalidOperationException("异常!不能重复对一个单元格进行赋值!");
}
if (cell.Candidate.Count == 0)
{
return false;
}
//随机选取单元格中的一个候选数为值,并移除该候选数
series = random.Next(0, cell.Candidate.Count - 1);
cell.Value = cell.Candidate[series];
cell.Candidate.RemoveAt(series);
return true;
}
这里我们事先对单元格逻辑进行了异常处理:
1.如果是这个单元格的值不等于0,那证明这个单元格是已经有值的,于是我们便不能为它赋值了!
2.如果这个单元格的候选数列表的个数为0,则表示这个单元格没有候选数可选了,这就意味着这个单元格取1~9这9个数都不会满足要求,这是我们返回一个标志false,表示赋值失败。
还要注意一点就是,这里我们定义了一个series变量,他是产生的一个随机数。其实最初我这个程序是直接写0,即是永远取候选数列表中的第一个赋值,并移除第一个候选数。但是那样每次都会生成一样的数独,因为取数的顺序是一样的,每次生成的结果必然一样。所以这里用到了一个随机产生的数,每次为单元格赋值的时候,随机从候选数列表中取一个数赋值,这样每次运行这个程序生成的数独都不会一样了。
这里series变量和random变量都是定义在类中的,而没定义在方法中,所以截图中没有他们的定义。
RemoveCellCandidate
下面我们将一起来看移除单元格候选数的方法:
 代码
代码
/// 移除单元格的候选数
/// </summary>
/// <param name="table">表</param>
/// <param name="i">行</param>
/// <param name="j">列</param>
/// <param name="index">索引</param>
/// <returns>返回结果</returns>
static private bool RemoveCellCandidate(Cell[,] table, int i, int j, int index)
{
int value = table[index / 9, index % 9].Value;
bool flag = true;
if (table[i, j].Candidate.Contains(value))
{//如果单元格候选数有此数,移除之
table[i, j].Candidate.Remove(value);
if (table[i, j].Candidate.Count == 0 && table[i, j].Value == 0)
{//如果单元格移除此候选数之后,并未赋值且候选数量为0,则失败,回滚
flag = false;
}
}
else if (table[i, j].DuplicateDel.ContainsKey(value))
{//如果单元格候选数没有此数,且在重复删除的字典里有此数,则重复删除字典此数对应的键值的值+1
table[i, j].DuplicateDel[value]++;
}
else
{//如果单元格候选数没有此数,且在重复删除的字典里没有此数,则重复删除字典添加此数的键值,并赋值为1
table[i, j].DuplicateDel.Add(value, 1);
}
return flag;
}
这个方法有很多东西要说,一个一个来。table表示这个9*9的二维数独,所以它的类型是Cell[,],我们定义的时候定义的是Cell[9,9]。i,j表示这个要处理的单元格的行列标号,即第i行第j列(从0开始数)。index表示被赋值的那个单元格的索引。这个索引需要解释一下,从第一行开始数,数完一行换行继续数,具体的索引对应单元格见下图:
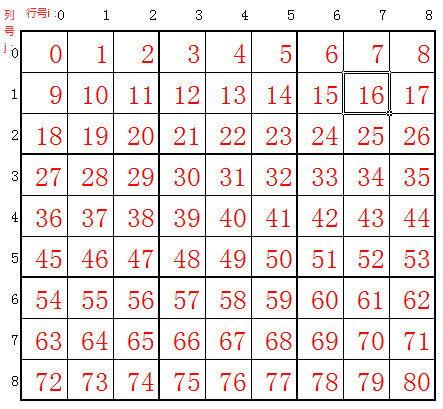
其实索引也可以用i,j来表示:如果是对应同一个单元格,index=i*9+j;
i,j当然也可以用索引表示:i=index/9,j=index%9("/"表示除后的商,"%"表示除后的余数)。但是,此处的index和i,j是指的不同的单元格。例如:我们需要为单元格A赋值,假设从A的候选数中我们选出了值1,那么我们将需要找到与单元格A相关(相关的意义见文章一)的其他单元格,将这些单元格中的候选数1移除。假如现在我们发现单元格B与单元格A相关,那么我们要移除B中的候选数1,这是我们为这个方法传递的参数i,j就是B的行列标号1,3,参数index就是A的索引31,见下图:
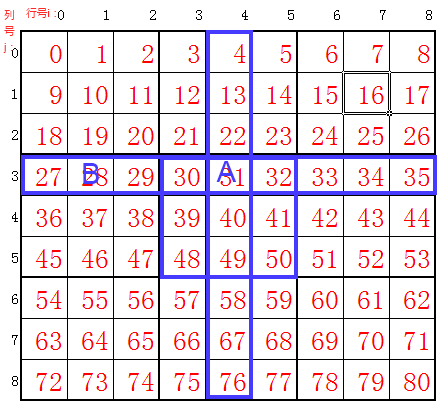
其中用蓝色框起来的区域,除了A本身以外,都是叫A的相关单元格。B只是其中一个。
现在我们再看看这个方法里我们都做了些什么事。假设当我们为单元格A赋值1的时候,我们需要更新单元格A的相关单元格的候选数,这就是我们这个方法要做的。我们现在只讨论单元格B的变动,其他相关单元格变动与B一样。
情况1.假设在为A赋值之前,B有候选数1,2,3,6,8,9。为A赋值之后,B的候选数将变为2,3,6,8,9。候选数1将被移除。
情况2.假设在为A赋值之前,B有候选数2,3,6,8,9。为A赋值之后,B的候选数将还是2,3,6,8,9。
这样将会产生一个问题!如果是A赋值1后,我们发现无论如何都不能成功生成数独,那么我们便知道,A的值不能等于1。这时我们便需要为A重新赋值另外一个数。而这个时候,与A相关的单元格会有什么变化呢?既然A不等于1了,那也就是说,A的相关单元格的候选数1又可以使用了。我们把它称为候选数的还原。这时,如果是情况1,B的候选数会正确还原到为A赋值之前的状态。但如果是情况2,就不那么走运了。在为A赋值之前,B本身就没有候选数1,但这时如果恢复候选数,那么B的候选数将变为1,2,3,6,8,9。这很明显不是最开始B的状态,所以属性DuplicateDel就诞生了,它就是用来处理这个问题的!看下面的图:
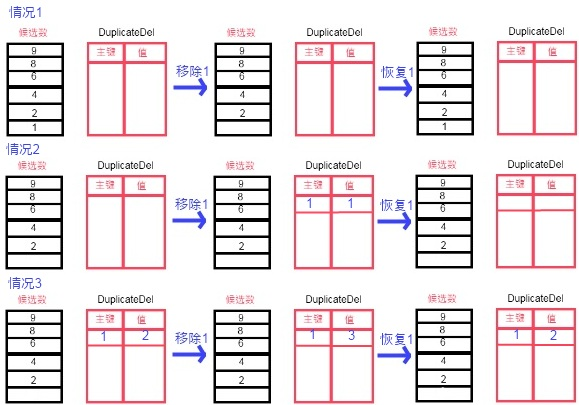
情况1就不用解释了,我主要说明一下情况2、3。
情况2就是刚才我们所说的情况,现在有了属性DuplicateDel就好办了,如果是在移除候选数1时我们发现B中候选数本来就没有1,那么就去找DuplicateDel列表,看里面有没有主键是1的,发现没有,那么我们就添加一条记录,主键是1,值是1,表示1这个候选数我们重复删除了1次。在恢复的时候,我们先去找DuplicateDel列表,看里面有没有主键是1的。发现有一条,那么就把他的值减一,如果减完后发现主键1的值为0,那么把它从DuplicateDel列表中删除。
情况3是另一种情况,我们首先发现候选数没有1,又发现DuplicateDel列表中已经有了主键1,他的值为2,这就意味着1这个候选数已经被重复删除了2次了。现在我们又要删除1,说明这将是1的第3次,因此DuplicateDel列表中为主键1的值加1,变成3。当我们要恢复时,便再从主键1的值中减去1。
以上三种情况包括了所有删除候选数1的情况,由图可以看出,有了DuplicateDel列表,我们都可以完美的移除候选数,恢复候选数,而不会引起错误。
本篇内容讲了2个方法,一个SetValue,一个RemoveCellCandidate,下一篇我们将讲述另外两个方法:恢复候选数RecoverCellCandidate和处理相关单元格DealRelativeCell
