1.混淆矩阵(confusion matrix)
针对预测值和真实值之间的关系,我们可以将样本分为四个部分,分别是:
真正例(True Positive,TP):预测值和真实值都为1
假正例(False Positive,FP):预测值为1,真实值为0
真负例(True Negative,TN):预测值与真实值都为0
假负例(False Negative,FN):预测值为0,真实值为1
我们将这四种值用矩阵表示(图片引自《machine learning:A Probabilistic Perspective》):
上面的矩阵就是混淆矩阵。
2.ROC曲线
通过混淆矩阵,我们可以得到真正例率(True Positive Rate , TPR):
我们还可以得到假正例率(False Positive Rate , FPR):
可以看到,TPR也就是我们所说的召回率,那么只要给定一个决策边界阈值![]() ,我们可以得到一个对应的TPR和FPR值,然而,我们不从这个思路来简单的得到TPR和FPR,而是反过来得到对应的
,我们可以得到一个对应的TPR和FPR值,然而,我们不从这个思路来简单的得到TPR和FPR,而是反过来得到对应的![]() ,我们检测大量的阈值
,我们检测大量的阈值![]() ,从而可以得到一个TPR-FPR的相关图,如下图所示(图片引自《machine learning:A Probabilistic Perspective》):
,从而可以得到一个TPR-FPR的相关图,如下图所示(图片引自《machine learning:A Probabilistic Perspective》):
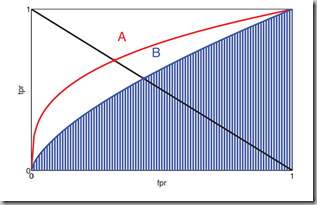
图中的红色曲线和蓝色曲线分别表示了两个不同的分类器的TPR-FPR曲线,曲线上的任意一点都对应了一个![]() 值。该曲线就是ROC曲线(receiver operating characteristic curve)。该曲线具有以下特征:
值。该曲线就是ROC曲线(receiver operating characteristic curve)。该曲线具有以下特征:
- 最完美的分类器(完全区分正负样例):(0,1)点,即没有FP,全是TP
- 曲线越是“凸”向左上角,说明分类器效果越好
- 随机预测会得到(0,0)和(1,1)的直线上的一个点
从图中可以看出,红色曲线所代表的分类器效果好于蓝色曲线所表示的分类器。
3.利用ROC的其他评估标准
- AUC(area under thecurve),也就是ROC曲线的下夹面积,越大说明分类器越好,最大值是1,图中的蓝色条纹区域面积就是蓝色曲线对应的 AUC
- EER(equal error rate),也就是FPR=FNR的值,由于FNR=1-TPR,可以画一条从(0,1)到(1,0)的直线,找到交点,图中的A、B两点。
参考:
1.《machine learning:A Probabilistic Perspective》
2.wiki