题目来源: Ural 1318
给出n个互不相等的整数A[0] - A[n-1],选A[i]同A[j]进行异或运算(结果都 > 0无符号),对结果取lg(以10为底)并取整后记为L[i,j],求n个数之间两两运算得到的L[i,j]之和。
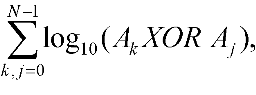
例如:1 10 30,1 xor 10 = 11,10 xor 30 = 20,1 xor 30 = 31。Sum = Lg(11) * 2 + Lg(20) * 2 + Lg(30) * 2 = (1 + 1 + 1) * 2 = 6(取整)。
由于i j同j i算作2个不同的,因此最终结果要 * 2。
Input
第1行:1个数N,表示整数的数量。(2 <= N <= 50000)
第2 - N + 1行:每行个1数A[i](1 <= A[i] <= 10^18)
Output
输出两两异或后取Lg(以10为底)并取整后的和。
首先建出二进制trie,然后由数据范围知log10(A[i] xor A[j])在0到19,可以枚举每个数和log10的每个取值在trie上查询出现次数
#include<cstdio> typedef long long i64; i64 _(){ i64 x=0; int c=getchar(); while(c<48)c=getchar(); while(c>47)x=x*10+c-48,c=getchar(); return x; } const int N=50007*65; int n; i64 a[50007]; int ch[N][2],sz[N],ptr=1; i64 ts[20],p10[20]; void ins(i64 x){ int w=1; for(int i=62;~i;i--){ int d=x>>i&1; if(!ch[w][d])ch[w][d]=++ptr; w=ch[w][d]; ++sz[w]; } } int find(i64 x,i64 y){ int s=0,w=1; for(int i=62;~i;i--){ int d1=x>>i&1,d2=y>>i&1; if(d2)s+=sz[ch[w][d1^d2^1]]; w=ch[w][d1^d2]; } return s; } int main(){ n=_(); for(int i=0;i<n;i++){ a[i]=_(); ins(a[i]); } p10[0]=1; for(int i=1;i<=18;i++)p10[i]=p10[i-1]*10; for(int i=0;i<n;i++){ for(int j=1;j<=18;j++)ts[j]+=find(a[i],p10[j]); } ts[19]=1ll*n*n-ts[18]; for(int i=18;i>1;i--)ts[i]-=ts[i-1]; ts[1]-=n; i64 ans=0; for(int i=2;i<=19;i++)ans+=(i-1)*ts[i]; printf("%lld",ans); return 0; }