Dynamic programming——自下而上 VS. 自上而下

转载至CSDN

https://blog.csdn.net/u013309870/article/details/75193592

动态规划算法的两种形式

上面已经知道动态规划算法的核心是记住已经求过的解，记住求解的方式有两种：①自顶向下的备忘录法 ②自底向上。
为了说明动态规划的这两种方法，举一个最简单的例子：求斐波拉契数列Fibonacci 。先看一下这个问题：

Fibonacci (n) = 1;   n = 0

Fibonacci (n) = 1;   n = 1

Fibonacci (n) = Fibonacci(n-1) + Fibonacci(n-2)

以前学c语言的时候写过这个算法使用递归十分的简单。先使用递归版本来实现这个算法：

public int fib(int n)
{
    if(n<=0)
        return 0;
    if(n==1)
        return 1;
    return fib( n-1)+fib(n-2);
}
//输入6
//输出：8

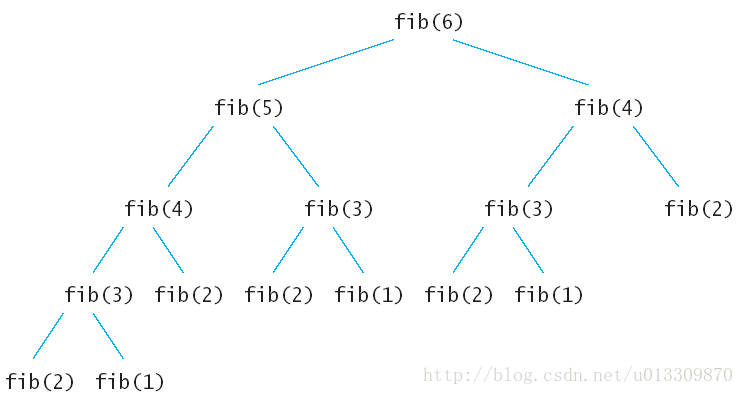
先来分析一下递归算法的执行流程，假如输入6，那么执行的递归树如下：

上面的递归树中的每一个子节点都会执行一次，很多重复的节点被执行，fib(2)被重复执行了5次。由于调用每一个函数的时候都要保留上下文，所以空间上开销也不小。这么多的子节点被重复执行，如果在执行的时候把执行过的子节点保存起来，后面要用到的时候直接查表调用的话可以节约大量的时间。下面就看看动态规划的两种方法怎样来解决斐波拉契数列Fibonacci 数列问题。

①自顶向下的备忘录法

public static int Fibonacci(int n)
{
        if(n<=0)
            return n;
        int []Memo=new int[n+1];        
        for(int i=0;i<=n;i++)
            Memo[i]=-1;
        return fib(n, Memo);
    }
    public static int fib(int n,int []Memo)
    {

        if(Memo[n]!=-1)
            return Memo[n];
    //如果已经求出了fib（n）的值直接返回，否则将求出的值保存在Memo备忘录中。               
        if(n<=2)
            Memo[n]=1;

        else Memo[n]=fib( n-1,Memo)+fib(n-2,Memo);  

        return Memo[n];
    }

备忘录法也是比较好理解的，创建了一个n+1大小的数组来保存求出的斐波拉契数列中的每一个值，在递归的时候如果发现前面fib（n）的值计算出来了就不再计算，如果未计算出来，则计算出来后保存在Memo数组中，下次在调用fib（n）的时候就不会重新递归了。比如上面的递归树中在计算fib（6）的时候先计算fib（5），调用fib（5）算出了fib（4）后，fib（6）再调用fib（4）就不会在递归fib（4）的子树了，因为fib（4）的值已经保存在Memo[4]中。

②自底向上的动态规划

备忘录法还是利用了递归，上面算法不管怎样，计算fib（6）的时候最后还是要计算出fib（1），fib（2），fib（3）……,那么何不先计算出fib（1），fib（2），fib（3）……,呢？这也就是动态规划的核心，先计算子问题，再由子问题计算父问题。

public static int fib(int n)
{
        if(n<=0)
            return n;
        int []Memo=new int[n+1];
        Memo[0]=0;
        Memo[1]=1;
        for(int i=2;i<=n;i++)
        {
            Memo[i]=Memo[i-1]+Memo[i-2];
        }       
        return Memo[n];
}

自底向上方法也是利用数组保存了先计算的值，为后面的调用服务。观察参与循环的只有 i，i-1 , i-2三项，因此该方法的空间可以进一步的压缩如下。

public static int fib(int n)
    {
        if(n<=1)
            return n;

        int Memo_i_2=0;
        int Memo_i_1=1;
        int Memo_i=1;
        for(int i=2;i<=n;i++)
        {
            Memo_i=Memo_i_2+Memo_i_1;
            Memo_i_2=Memo_i_1;
            Memo_i_1=Memo_i;
        }       
        return Memo_i;
    }

一般来说由于备忘录方式的动态规划方法使用了递归，递归的时候会产生额外的开销，使用自底向上的动态规划方法要比备忘录方法好。