推荐博客 : http://blog.csdn.net/zlambert/article/details/65691838
为了避免重复的计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
两个集合的容斥关系公式:A∪B = A+B – A∩B (∩:重合的部分)
三个集合的容斥关系公式:A∪B∪C = A+B+C – A∩B – B∩C – C∩A +A∩B∩C
四个集合的容斥关系公式:A∪B∪C∪D = A+B+C+D – A∩B – A∩C – A∩D - B∩C-B∩D-C∩D +A∩B∩C+A∩B∩D+A∩C∩D+B∩C∩D - A∩B∩C∩D.
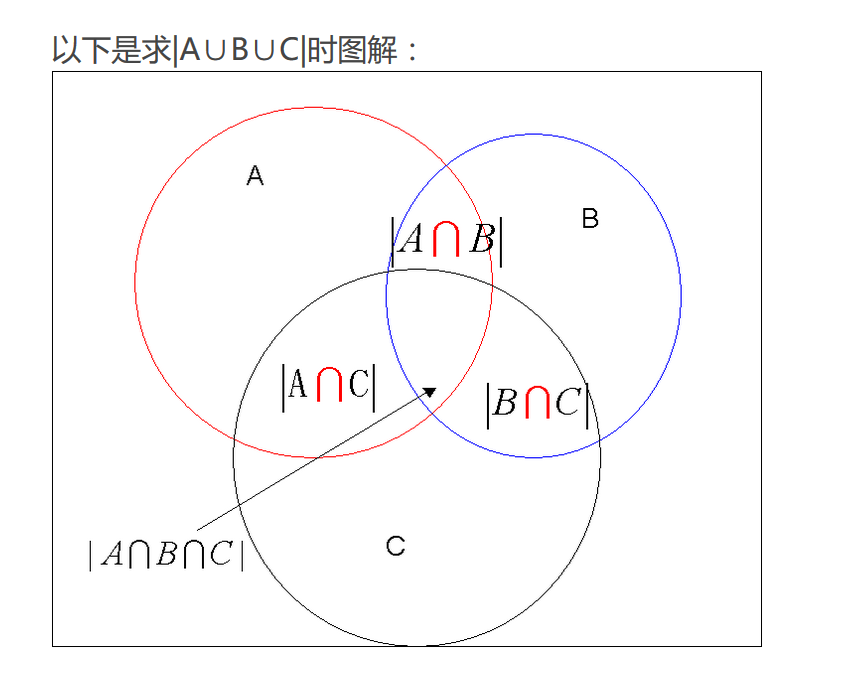
容斥原理的应用 :
二维前缀和 :
【程序1】数阵和 一个n*m的数阵,求前i行前j列所有数的和
输入:
第一行两个整数n和m(0 <= n,m <=1000);
接下来n行,每行m个整数;
最后一行两个整数i和j
输出:
一个整数,前i行前j列所有数的和。
输入样例:
3 4
1 4 2 7
6 8 1 9
5 4 3 10
2 2
输出样例:
19
根据容斥原理,可得递推公式:f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+a[i,j]