最经典的用法是 用来求一个三角形的面积或是判断个方向
去年的省赛有一个题目是求一个多边型的面积,在这里,用叉积就可以轻松解决
现有一个问题,让你去判断一个点是否在三角形的内部,在这里介绍三种方法 (推荐博客 : http://www.cnblogs.com/TenosDoIt/p/4024413.html)
1 . 面积法
若点在三角形的内部,则由 p 点构成的三个三角形的面积等于整个三角形的面积,若不相等,则 p 不在三角形的内部。
2 . 叉积判断方向法
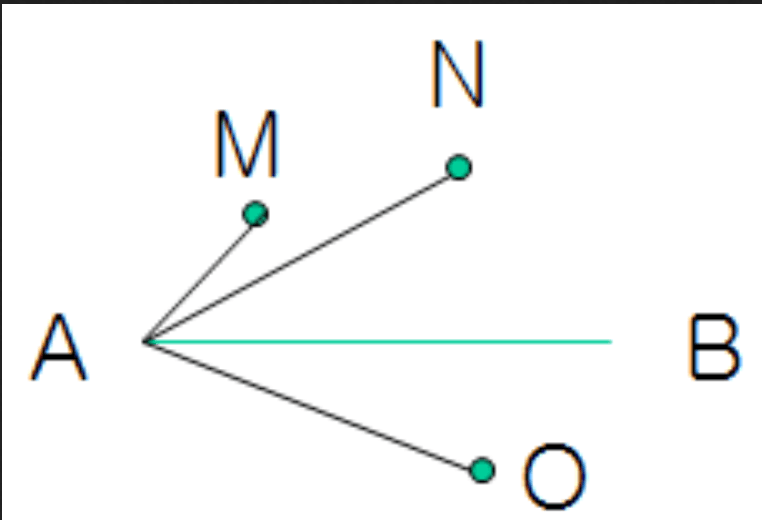
向量 AM 叉乘 向量 AB 的方向设为正,则向量 AN 叉乘 向量 AB的方向也为正,则说明 M 与 N在直线AB的同一侧,那么向量 AO 与向量 AB 的叉积则会为负。说明 N 与 O 不在同一侧。
3 . 叉积判断法的优化
首先求出 向量 PA, PB, PC, 再分别计算向量 PA 叉乘 PB, PB 叉乘 PC, PC叉乘PA,若方向全为正或者全为负,则 P 在内部,否则P在外部。
叉积判断点在直线的左侧还是右侧
当叉积相乘的方向若垂直平面向外时,所计算出的向量是为正值,此时所要判断的点在直线的左侧